Epidemia SARS 2003 en Hong Kong
Imagen
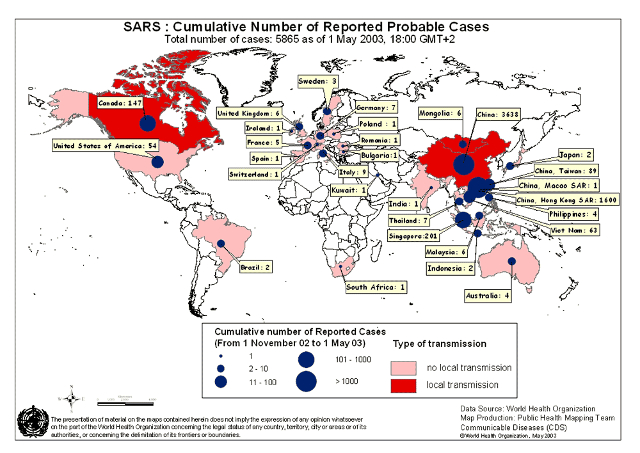
En el 2003 se produce en China un brote de SARS (Severe acute respiratory syndrome) que se propaga a Hong Kong y luego al mundo entero. En el siguiente mapa se ve la cantidad de casos en los distintos países:
ID:(9662, 0)
Simulador SARS - ajuste de un Modelo SEIR
Php
El presente simulador contiene los datos de la epidemia de SARS para el caso de Hong Kong y permite buscar los parámetros de un modelo SEIR ajustando las curvas a los valores reales:
ID:(9659, 0)
Análisis epidemia SARS 2003 en Hong Kong
Imagen
Si se estudia los datos de la WHO para la epidemia de SARS en 2003 en Hong Kong se puede estimar el numero actual de infectados
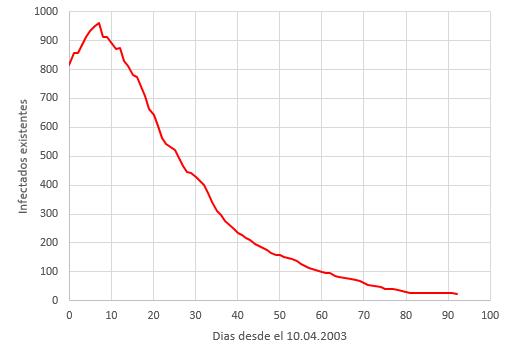
\\n\\nAun cuando no se tiene la sección del inicio se observa el máximo típico del número de infectados cuando se comienza a controlar estos y se da que\\n\\n
$\displaystyle\frac{dS}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I=0$
\\n\\npor lo que los susceptibles en dicho punto alcanzan\\n\\n
$S=\displaystyle\frac{\gamma}{\beta C}N$
ID:(8202, 0)
Determinación de Parametros SARS 2003 en Hong Kong
Imagen
Si se estudia la forma como descienden los infectados se ve que al avanzar el tiempo debe dominar el termino gamma ya que es el que reduce el volumen total que describe el primer termino. Por ello se tiene que para tiempos en que la epidemia esta bajo control\\n\\n
$\displaystyle\frac{dI}{dt}=\left(\displaystyle\frac{\beta C}{N}S-\gamma\right)I\sim-\gamma I$
\\n\\nEn ese caso la solución asintomática es de la forma\\n\\n
$I(t) \propto e^{-\gamma t}$
lo que se aprecia en la curva de los infectados existentes para el caso SARS 2003 en Hong Kong. Por ello se puede hacer un ajuste por mínimos cuadrados de la parte final de la curva
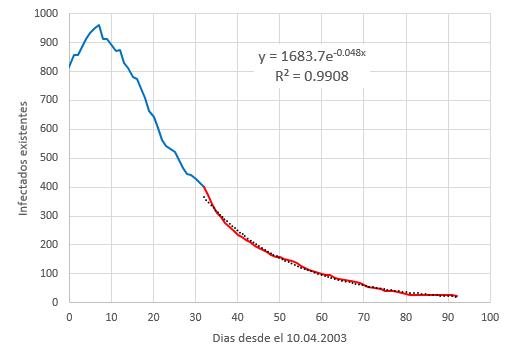
\\n\\nobteniendo se que el factor
$\tau=\displaystyle\frac{1}{\gamma}\sim 20.8,dias$
Si además asumimos que cada persona se reúne a diario con del orden de 30 personas, se tendría que el factor
ID:(8203, 0)
Modelo SIR para describir SARS 2003 en Hong Kong
Imagen
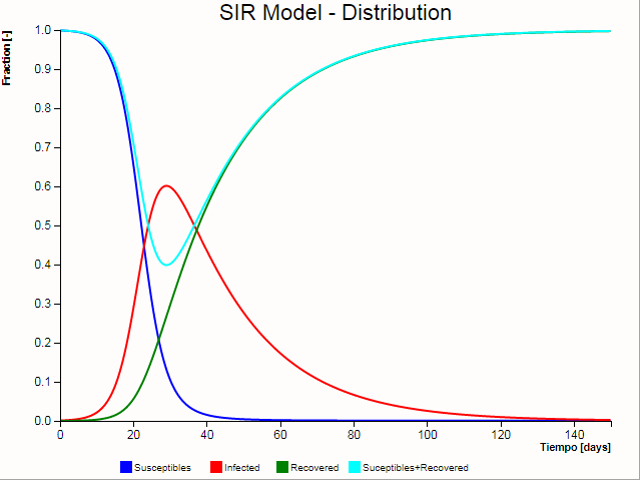
Si se observan los susceptibles, infectados y 'recuperados' (que se sanan o mueren) se observan las típicas curvas del modelo SIR:
ID:(9663, 0)
Datos ajustados
Imagen
Si se varían los parámetros de contagio y desarrollo se logra ajustar las sumas de:
• los infectados
• los recuperados
• los muertos
según muestra la siguiente imagen:

ID:(9693, 0)
Efecto de incrementar N
Imagen
Si el numero de personas que pertenecen al grupo en que se propaga la enfermedad es muy grande la curva tiende a sobrepasar los datos medidos:

ID:(9694, 0)
Efecto de reducir N
Imagen
Si el numero de personas que pertenecen al grupo en que se propaga la enfermedad es muy chico, la curva tiende a sobrepasar los datos medidos:

ID:(9695, 0)
Efecto de incrementar $\beta C$
Imagen
Si el numero de contactos y la tasa de contagio es demasiado grande la pendiente es demasiado grande (muy empinado):

ID:(9696, 0)
Efecto de reducir $\beta C$
Imagen
Si el numero de contactos y la tasa de contagio es demasiado pequeño la pendiente es demasiado chica (muy plano):

ID:(9697, 0)
Desfase temporal
Descripción
El tiempo de retraso permite desplazar la curva transportándola sin deformación a lo largo del eje del tiempo. Es necesaria ya que se desconoce el tiempo en que la enfermedad se ha iniciado y existe para cada una de las curvas en forma individual.\\n\\nCada curva se desplaza individualmente en los tiempos: \\n\\n• $t_{\rho}$ tiempo en que aparece el primer latente\\n• $t_{\beta}$ tiempo en que aparece el primer infectados\\n• $t_{\gamma}$ tiempo en que aparece el primer recuperado\\n• $t_{\delta}$ tiempo en que aparece el primer muerto\\n\\nEn general debiese eser que los tiempos son tales que\\n\\n
$t_{\rho} < t_{\beta} < t_{\gamma} < t_{\delta}$
dada la secuencia de los eventos en el modelo. Sin embargo el ajuste y la incerteza en los datos pueden dar ordenes distintos que señalan que los tiempos en si no son confiables.
Importante es reconocer de que el desface puede ser tanto positivo como negativo.
ID:(9702, 0)
Efecto de tiempo de retraso muy grande, ejemplo de infección
Imagen
Si el tiempo de retraso de cada curva es elegido demasiado grande la curva se atrasa respecto de la evolución real:

ID:(9698, 0)
Efecto de tiempo de retraso muy chico, ejemplo de infección
Imagen
Si el tiempo de retraso de cada curva es elegido demasiado chico la curva se adelante respecto de la evolución real:

ID:(9699, 0)
Efecto de tasa de recuperación y/o termino de latencia
Imagen
Si la tasa de recuperación y la de latencia son demasiado grandes la curva de infectados se vuelve mas empinada mientras que la de recuperación se aplana. En ese sentido estos factors parecen rotar ambas curvas aumentando (si crecen) y decreciendo (si disminuyen) el angulo que hay entre estas.

ID:(9700, 0)
Efecto de tasa muerte
Imagen
Si la tasa de muertos crece la correspondiente curva tiene una participación mayor en la población que ya no infecta y que se denomina en forma genérica 'recuperados':

ID:(9701, 0)
