Physik lernen wie mit LEGO spielen
Storyboard 
Physik ist eine Wissenschaft, die es uns ermöglicht, Situationen und Entwicklungen von Systemen in der realen Welt zu beschreiben. Sie basiert auf Variablen, die gemessen werden können, und Gleichungen, die sie miteinander in Beziehung setzen und somit ihre Berechnung und Vorhersage ermöglichen.
Jede Variable kann mit einem LEGO-Stein verglichen werden, der zusammengesetzt wird, um Gleichungen zu bilden, die einem funktionalen Element entsprechen. Diese verschiedenen Gleichungen ermöglichen es uns, ein Modell zu konstruieren, das einem LEGO-Spielzeug ähnelt und auf verschiedene Arten verwendet werden kann.
Die verschiedenen Verwendungsweisen entsprechen den möglichen Berechnungen, die mit unterschiedlichen Datensätzen und erforderlichen Zwischenberechnungen durchgeführt werden können.
Die Verwendung dieses Modells bezieht sich auf das, was wir in der Physik als Problem lösen bezeichnen.
ID:(1931, 0)
Die Analogie
Konzept 
Wir können eine Analogie zwischen einer realen Situation und einem LEGO-Spielzeug herstellen.

Die Analogie zwischen der Realität in Form einer Reise und einem LEGO-Spielzeug
In der physikalischen Situation werden Variablen und Gleichungen beschrieben, die sie verbinden.
Das LEGO-Spielzeug hingegen verwendet Bausteine und Teile, die zusammengebaut werden, um das Modell zu bilden.
Jeder Baustein entspricht somit einer Variablen, die verschiedene Teile verbindet, ähnlich wie es Gleichungen tun.
ID:(14372, 0)
Die Variablen
Konzept 
Wenn die Modellierung eines fahrenden Fahrzeugs betrachtet wird, müssen die Anfangsposition $s_0$ und die endgültig erreichte Position $s$ eingegeben werden:
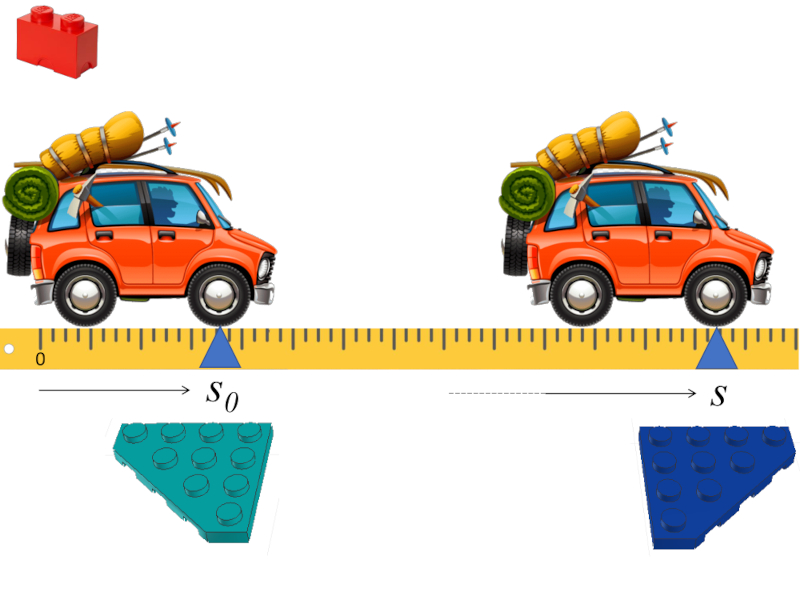
Die Analogie zwischen Variablen und LEGO-Steinen
Innerhalb der Analogie ist jeder Variablen ein LEGO-Stein zugeordnet. Da es sich um unterschiedliche Variablen handelt, werden sie in diesem Fall durch ihre Farbe unterschieden.
ID:(14373, 0)
Die Gleichungen: die Position
Konzept 
Innerhalb des Modells ist es sinnvoll, den zurückgelegten Weg $\Delta s$ zu berechnen.
Dazu muss ein neuer LEGO-Stein in die Analogie eingeführt werden.
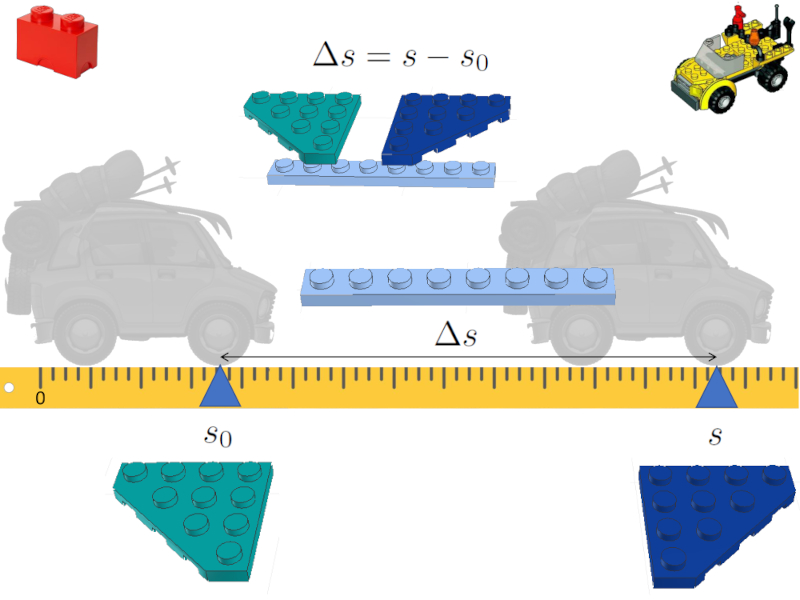
Die Analogie zwischen Gleichungen und LEGO-Sets
Für seine Berechnung muss die entsprechende Gleichung definiert werden, die in diesem Fall entspricht
$\Delta s = s - s_0$
In unserer Analogie werden LEGO-Steine verbunden, um die erste Einheit unseres Modells zu bilden.
ID:(14374, 0)
Die Gleichungen: Zeit
Konzept 
Um die Bewegung in unserem Modell zu beschreiben, ist es notwendig, die Zeit einzuführen.
Analog zur Position muss eine Startzeit $t_0$, die Endzeit $t$ und die abgelaufene Zeit $\Delta t$ eingegeben werden.
Jede der Variablen entspricht einem LEGO-Stein, der im Bild dargestellt ist:
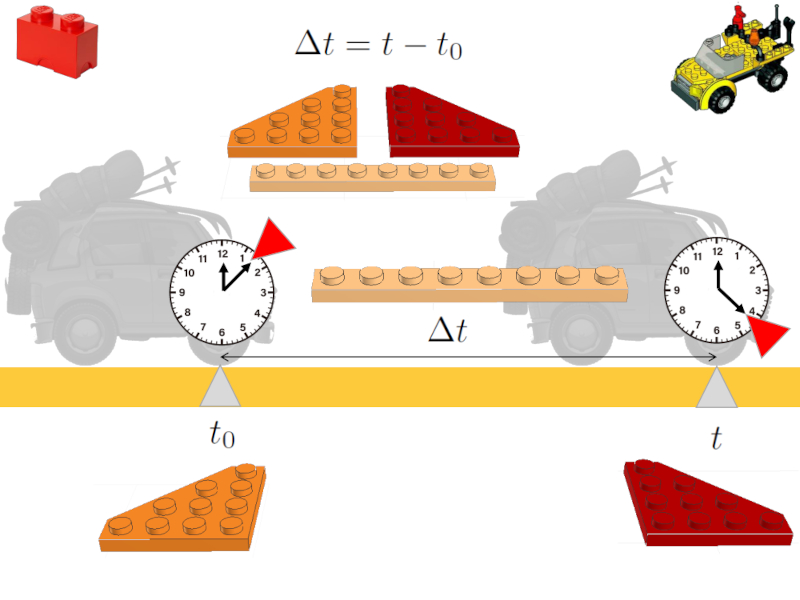
Die Einführung der Zeit und die Analogie zu LEGO
Zusätzlich muss die verstrichene Zeit eingegeben werden, die eine Gleichung der Form ist
$\Delta t = t - t_0$
Diese wiederum stellt in der Analogie eine neue Einheit des LEGO-Modells dar.
ID:(14375, 0)
Die Gleichungen: Geschwindigkeit
Konzept 
Um vorherzusagen, wie sich das Fahrzeug bewegen wird, müssen Sie die Geschwindigkeit eingeben.
Diese ist definiert als das Verhältnis der zurückgelegten Strecke zur verstrichenen Zeit.
Innerhalb der Analogie werden die Steine des zurückgelegten Weges mit denen der verstrichenen Zeit genommen und auf einen neuen Stein montiert, der die Geschwindigkeit darstellt:
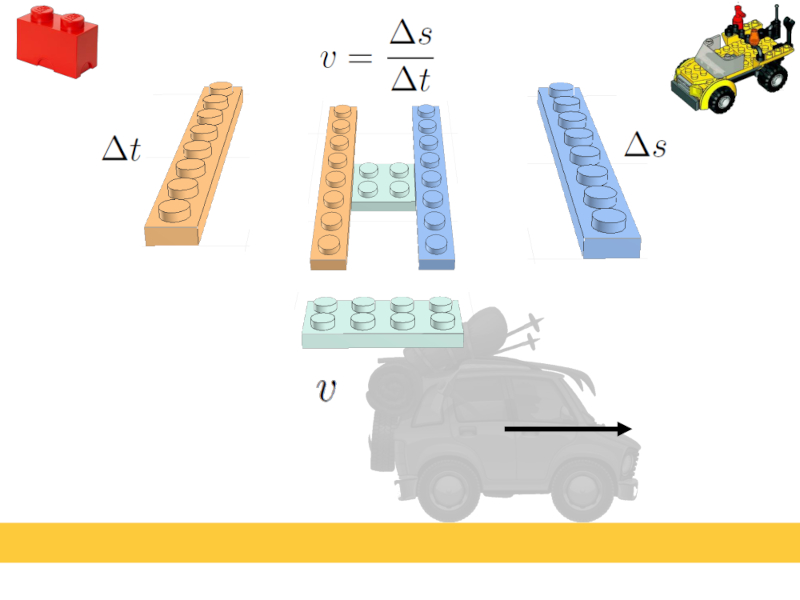
Die Analogie für die Einführung von Geschwindigkeit
Somit wird die dritte Gleichung eingeführt
$v = \displaystyle\frac{\Delta s}{\Delta t}$
ID:(14376, 0)
Alle Gleichungen
Konzept 
Wenn Sie mit dem Zusammenbau des LEGO-Modells fertig sind, erhalten Sie zusätzliche Beziehungen, die anderen Beschreibungen von Steingruppen entsprechen.
Auf diese Weise wird das Modell durch die bereits definierten fünf Variablen und durch insgesamt vier Gleichungen repräsentiert:
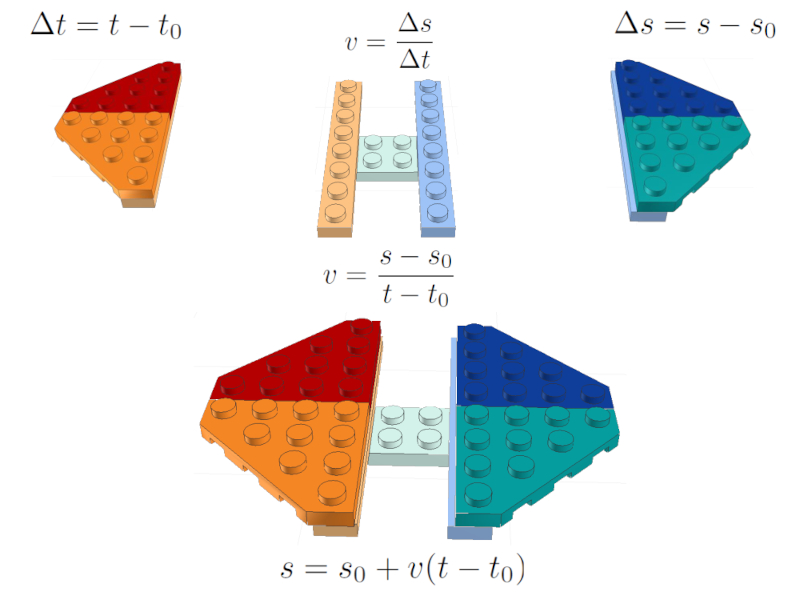
Satz aller Gleichungen
Der mittlere Teil zeigt die zusätzliche Gleichung, die sich aus dem Zusammenbau des vollständigen Modells ergibt.
ID:(14377, 0)
Das Model
Konzept 
Schließlich haben wir das vollständige Modell, dh die Variablen und die Gleichungen, die sie verknüpfen.
Innerhalb der Analogie gibt es praktisch eine Art Bauanleitung eines LEGO-Modells, in der die benötigten Steine und die zu bauenden Elemente aufgelistet sind.
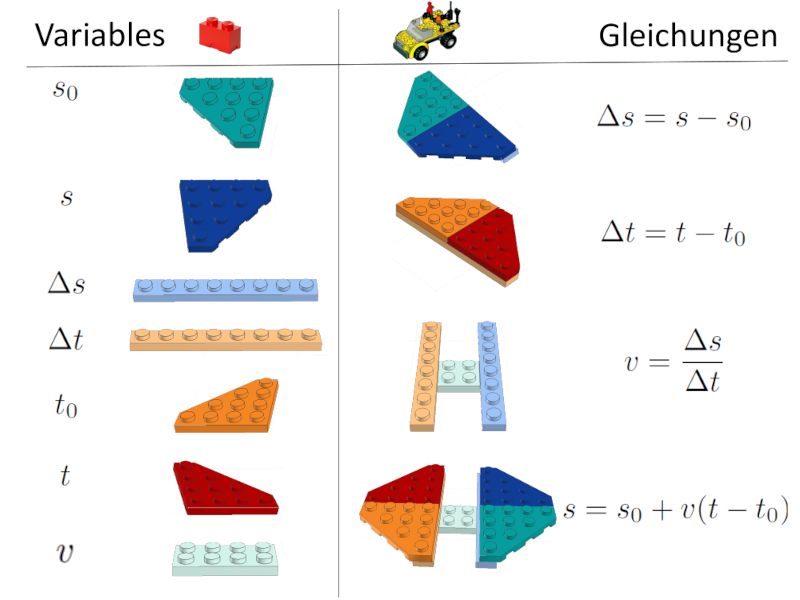
Anleitung des Modells im LEGO-Stil
ID:(14378, 0)
