Training Calorimetry
Storyboard 
To measure the heat capacity or specific heat of a metal, the metal is first submerged in boiling water and then in room temperature water. By analyzing the mass of the water and the changes in temperature, the thermal properties of the metal can be determined.
ID:(1315, 0)
Mechanisms
Definition 
Calorimetry is the practice of measuring heat involved in chemical reactions, physical changes, or heat capacity using a calorimeter. In this process, a well-insulated container is prepared to minimize heat exchange with the environment, and the substance or reaction of interest is placed inside. Once the reaction or process begins, the calorimeter is sealed to ensure no external heat influences the measurement. Temperature changes are carefully monitored with a thermometer or temperature sensor, and the mass and specific heat capacity of the substances involved are recorded. The heat absorbed or released by the substance is then calculated based on the observed temperature changes.
There are different types of calorimetry, such as constant-pressure calorimetry, bomb calorimetry, and differential scanning calorimetry (DSC), each suited for specific types of reactions and measurements. Applications of calorimetry include determining enthalpy changes in chemical reactions, measuring heat capacities and phase transitions, studying metabolic rates in biological systems, and characterizing materials by their thermal properties.
In essence, calorimetry involves preparing the experimental setup, initiating the process, measuring temperature changes precisely, and calculating heat transfer to analyze the thermal properties and behaviors of various substances and reactions.
ID:(15248, 0)
Experiment: container and sample diagram
Image 
Insulated calorimeter with a thermometer and sample inside the water. Beside it, a professional metal calorimeter.
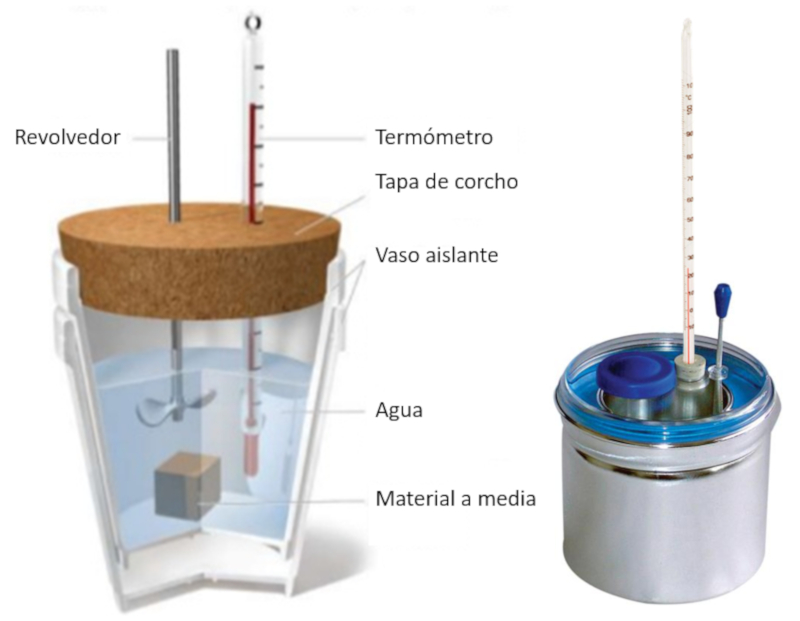
ID:(11120, 0)
Experiment: calorimetry procedure
Note 
Steps to perform the measurement:
Heat a defined quantity of ERROR:8084 until it reaches its boiling point.
Pour the water into an insulated container and measure its quantity (the hot water temperature ($T_i$)).
Weigh a sample of the body mass ($m$) that is at a temperature of the sample temperature ($T_m$).
Place the sample into the container and stir until it reaches the temperature of ERROR:8054.
Calculate the value of the specific heat of the sample ($c$).
Diagram:
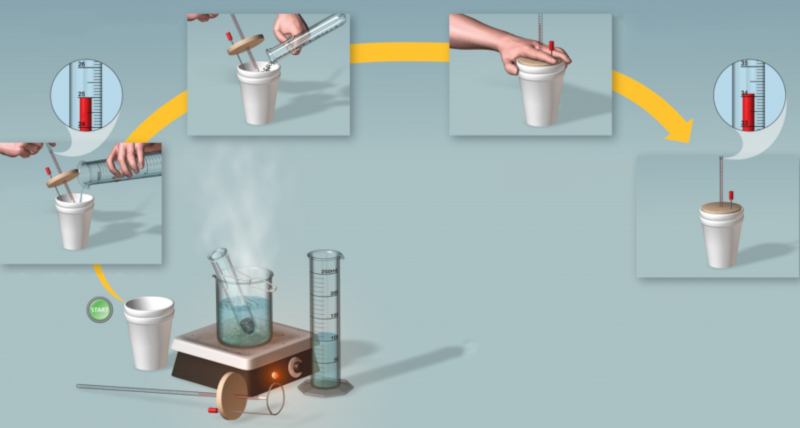
ID:(11119, 0)
Calorimetry in liquids and solids
Storyboard 
To measure the heat capacity or specific heat of a metal, the metal is first submerged in boiling water and then in room temperature water. By analyzing the mass of the water and the changes in temperature, the thermal properties of the metal can be determined.
Variables
Calculations
Calculations
Equations
The heat supplied to liquid or solid ($\Delta Q$) is related to the temperature variation ($\Delta T$) and the heat capacity ($C$) as follows:
Where the heat capacity ($C$) can be replaced by the specific heat ($c$) and the mass ($M$) using the following relationship:
Therefore, we obtain:
The heat supplied to liquid or solid ($\Delta Q$) is related to the temperature variation ($\Delta T$) and the heat capacity ($C$) as follows:
Where the heat capacity ($C$) can be replaced by the specific heat ($c$) and the mass ($M$) using the following relationship:
Therefore, we obtain:
The relationship between the amount of heat released by the object, represented as the heat difference ($\Delta Q$), with a mass of the body mass ($m$), and the temperatures the specific heat of the sample ($c$), ERROR:8054, and the sample temperature ($T_m$), can be described by the following equation:
This amount of heat is equal to the amount of heat absorbed by the water, which has a mass of ERROR:8084 and temperatures the specific heat of water ($c_w$), the hot water temperature ($T_i$), and ERROR:8054, and can be expressed by the equation:
These two amounts of heat are equal, so we can establish the following equality:
$m c (T_f - T_m) = M c_w (T_i - T_f)$
In this way, we can calculate the value of
Examples
Calorimetry is the practice of measuring heat involved in chemical reactions, physical changes, or heat capacity using a calorimeter. In this process, a well-insulated container is prepared to minimize heat exchange with the environment, and the substance or reaction of interest is placed inside. Once the reaction or process begins, the calorimeter is sealed to ensure no external heat influences the measurement. Temperature changes are carefully monitored with a thermometer or temperature sensor, and the mass and specific heat capacity of the substances involved are recorded. The heat absorbed or released by the substance is then calculated based on the observed temperature changes.
There are different types of calorimetry, such as constant-pressure calorimetry, bomb calorimetry, and differential scanning calorimetry (DSC), each suited for specific types of reactions and measurements. Applications of calorimetry include determining enthalpy changes in chemical reactions, measuring heat capacities and phase transitions, studying metabolic rates in biological systems, and characterizing materials by their thermal properties.
In essence, calorimetry involves preparing the experimental setup, initiating the process, measuring temperature changes precisely, and calculating heat transfer to analyze the thermal properties and behaviors of various substances and reactions.
Insulated calorimeter with a thermometer and sample inside the water. Beside it, a professional metal calorimeter.
Steps to perform the measurement:
Heat a defined quantity of ERROR:8084 until it reaches its boiling point.
Pour the water into an insulated container and measure its quantity (the hot water temperature ($T_i$)).
Weigh a sample of the body mass ($m$) that is at a temperature of the sample temperature ($T_m$).
Place the sample into the container and stir until it reaches the temperature of ERROR:8054.
Calculate the value of the specific heat of the sample ($c$).
Diagram:
In the calorimetric process, the sample cooling ($\Delta Q_m$) is equal to the water heating ($\Delta Q_w$):
The heat supplied to liquid or solid ($\Delta Q$) can be calculated with the specific heat ($c$), the mass ($M$) and the temperature variation ($\Delta T$) using:
The heat supplied to liquid or solid ($\Delta Q$) can be calculated with the specific heat ($c$), the mass ($M$) and the temperature variation ($\Delta T$) using:
If a system is initially at ERROR:5236.1 and then is at the temperature in final state ($T_f$), the difference will be:
The temperature difference is independent of whether these values are in degrees Celsius or Kelvin.
If a system is initially at ERROR:5236.1 and then is at the temperature in final state ($T_f$), the difference will be:
The temperature difference is independent of whether these values are in degrees Celsius or Kelvin.
If you wish to determine the value of the specific heat of the sample ($c$), you can achieve this by introducing an object with a mass of the body mass ($m$) into a mass of ERROR:8084 at the boiling point. Before doing so, measure the temperature of the object, which is typically at room temperature, denoted as the sample temperature ($T_m$), and then measure the temperature of the object submerged in water at the end of the process, denoted as ERROR:8054. Therefore, we know that the object has received a certain amount of ERROR:9840,0, which can be calculated using the formula:
Where the specific heat of the sample ($c$) is the value we want to determine. The heat the object has received comes from the water, whose temperature has decreased from the hot water temperature ($T_i$) to ERROR:8054. This can be expressed as:
Where the specific heat of water ($c_w$) represents the constant (1 cal/g = 4.186 J/g). By equating the amount of heat, we can determine the specific heat of the object using the following equation:
ID:(1315, 0)
