Entropia
Storyboard 
A entropia é a parte da energia em um sistema que não pode ser utilizada para realizar trabalho. Do ponto de vista microscópico, está relacionada com o número de possíveis configurações que o sistema pode assumir. Um maior número dessas configurações está associado a um aumento na desordem do sistema e a uma diminuição na probabilidade de que ele retorne a um estado anterior, reduzindo assim a possibilidade de reversibilidade do sistema.
ID:(1471, 0)
Mecanismos
Conceito 
A entropia física é um conceito fundamental na termodinâmica e na mecânica estatística que representa o grau de desordem ou aleatoriedade em um sistema. Ela mede o número de maneiras específicas pelas quais um sistema termodinâmico pode ser organizado, refletindo a quantidade de incerteza ou o número de possíveis microestados correspondentes a um dado macroestado. A entropia quantifica a desordem, sendo que uma maior entropia indica maior desordem. De acordo com a segunda lei da termodinâmica, a entropia de um sistema isolado nunca diminui, o que significa que os processos naturais tendem a se mover para um estado de entropia máxima ou desordem. A entropia também mede a irreversibilidade dos processos, onde processos espontâneos aumentam a entropia do universo. Ela é um fator chave para determinar a eficiência de motores térmicos e refrigeradores, entender o comportamento de sistemas biológicos e estudar a evolução do universo. Essencialmente, a entropia é uma medida da imprevisibilidade e da dispersão de energia em um sistema, fornecendo insights sobre a tendência natural para a desordem e as limitações na conversão de energia.
ID:(15246, 0)
Tipos de variáveis
Descrição 
Se considerarmos a equação de ERROR:5221,0 com la força mecânica ($F$) e o distância percorrida ($dx$):
| $ \Delta W = F \Delta s $ |
na sua forma de la pressão ($p$) e o volume ($V$):
| $ \delta W = p dV $ |
O trabalho desempenha o papel de um potencial, enquanto la pressão ($p$) age como uma 'força generalizada', e o volume ($V$) serve como o caminho, uma espécie de 'variável independente'. Se organizarmos esses conceitos em uma matriz para os parâmetros que discutimos até agora, obtemos:
| Potencial termodinâmico | Força generalizada | Variável independente |
| Extensiva | Intensiva | Extensiva |
| $\delta W$ | $p$ | $dV$ |
| $\delta Q$ | $T$ | $?$ |
Nesse contexto, vemos que para a linha la variação de calor ($\delta Q$), temos a variável la temperatura absoluta ($T$), mas falta-nos uma variável independente extensiva. A esta chamamos de entropia e a denotamos com a letra $S$.
ID:(11183, 0)
Variables intensives et extensives
Descrição 
Existem variáveis que estão associadas a quantidades e outras que estão associadas a propriedades.• As primeiras são chamadas de variáveis extensivas, pois podem ser estendidas ou aumentadas em proporção à quantidade de substância presente. Exemplos de variáveis extensivas incluem volume, massa, carga elétrica, calor, entre outros.• Por outro lado, as segundas são chamadas de variáveis intensivas, que representam propriedades que não dependem da quantidade de substância presente. Essas propriedades não se alteram quando a quantidade de substância é alterada. Exemplos de variáveis intensivas incluem densidade, pressão, temperatura, entre outros.
ID:(11182, 0)
Entropia e mudança de fase
Descrição 
Se a entropia for estimada em função da temperatura, as seguintes observações podem ser feitas:
• Em cada fase (sólido, líquido, gasoso), a entropia tende a aumentar ligeiramente com a temperatura.
• Durante as transições de fase, ocorre um salto significativo na entropia.
Isso pode ser representado da seguinte forma:
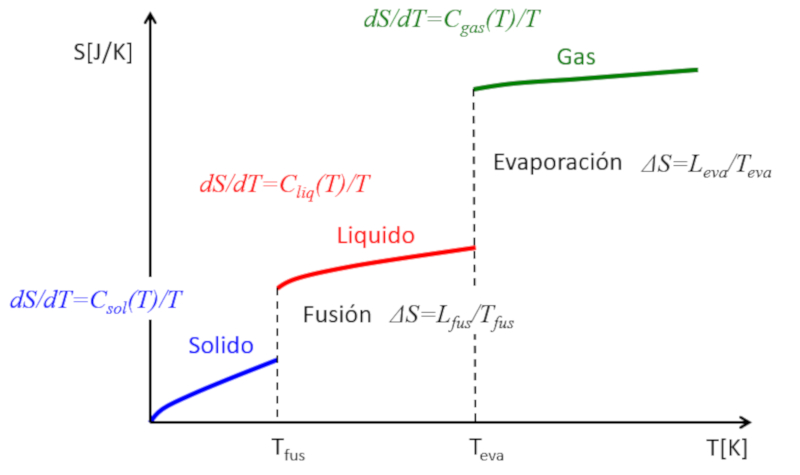
Dessa maneira, a entropia pode ser compreendida como uma medida média dos graus de liberdade que um sistema possui. Enquanto em cada fase a entropia aumenta gradualmente devido à liberação de alguns graus de liberdade adicionais, nas transições de fase o aumento é dramático. Um sólido é composto por múltiplas ligações que restringem o movimento dos átomos, resultando em poucos graus de liberdade. Em um líquido, muitas ligações são rompidas, criando novas liberdades que permitem o movimento relativo, levando a múltiplos novos graus de liberdade. Finalmente, na transição para a fase gasosa, todas as ligações são perdidas e cada partícula possui seus três graus de liberdade. À medida que a temperatura aumenta, as partículas podem rotacionar e oscilar, introduzindo novos graus de liberdade e incrementos adicionais na entropia.
ID:(11187, 0)
Entropia e Irreversibilidade
Descrição 
Se considerarmos dois sistemas idênticos, um com uma temperatura $T_1$ e o outro com uma temperatura $T_2$, suas entropias podem ser calculadas usando a seguinte equação envolvendo la entropia ($S$), la temperatura absoluta ($T$), la calor específico da amostra ($C$), la entropia básica ($S_0$) e la temperatura base ($T_0$):
| $ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$ |
Portanto, as entropias serão:
$S_1 = S_0 + C\log\left(\displaystyle\frac{T_1}{T_0}\right)$
e
$S_2 = S_0 + C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Se ambos os sistemas forem misturados, sua temperatura será a temperatura média:
$T_m=\displaystyle\frac{1}{2}(T_1+T_2)$
Portanto, a entropia do novo sistema será:
$S_{1+2}=2S_0+2C\log\left(\displaystyle\frac{T_m}{T_0}\right)=2S_0+2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)$
A entropia do novo sistema é maior do que a soma das entropias individuais:
$\Delta S=2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)-C\log\left(\displaystyle\frac{T_1}{T_0}\right)-C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Se representarmos graficamente $\Delta S/C$ em função de $T_1/T_0$ e $T_2/T_0," obtemos a seguinte figura:
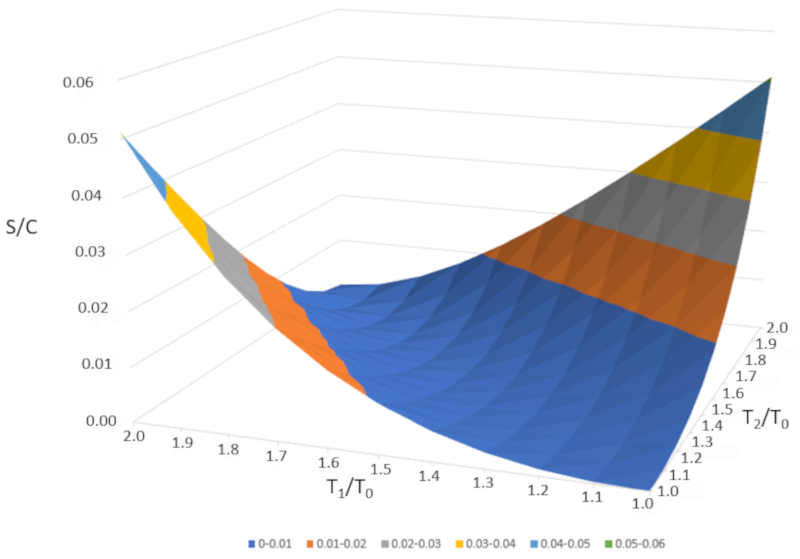
$\Delta S/C$ é quase nulo se as temperaturas forem muito semelhantes ($T_1\sim T_2$). No entanto, se as temperaturas forem diferentes, a entropia sempre aumentará. Se estudarmos isso em outros sistemas, observaremos que sempre que ocorre uma mudança irreversível, a entropia aumenta. A mistura é irreversível, o que significa que o sistema não retornará ao seu estado inicial sem intervenção externa. Em outras palavras, o sistema não se separará espontaneamente em dois subsistemas com temperaturas completamente diferentes.
ID:(11186, 0)
Entropia
Modelo 
A entropia física é um conceito fundamental na termodinâmica e na mecânica estatística que representa o grau de desordem ou aleatoriedade em um sistema. Ela mede o número de maneiras específicas pelas quais um sistema termodinâmico pode ser organizado, refletindo a quantidade de incerteza ou o número de possíveis microestados correspondentes a um dado macroestado. A entropia quantifica a desordem, sendo que uma maior entropia indica maior desordem. De acordo com a segunda lei da termodinâmica, a entropia de um sistema isolado nunca diminui, o que significa que os processos naturais tendem a se mover para um estado de entropia máxima ou desordem. A entropia também mede a irreversibilidade dos processos, onde processos espontâneos aumentam a entropia do universo. Ela é um fator chave para determinar a eficiência de motores térmicos e refrigeradores, entender o comportamento de sistemas biológicos e estudar a evolução do universo. Essencialmente, a entropia é uma medida da imprevisibilidade e da dispersão de energia em um sistema, fornecendo insights sobre a tendência natural para a desordem e as limitações na conversão de energia.
Variáveis
Cálculos
Cálculos
Equações
Exemplos
Para compreender melhor o conceito de entropia, podemos imaginar um sistema no estado s lido, onde os tomos est o organizados de forma ordenada e a entropia baixa.
medida que fornecemos energia ao sistema, os tomos come am a oscilar com mais intensidade, e a ordem come a a se perder. Ao atingir a temperatura de fus o, algumas part culas s o libertadas de suas posi es fixas e ganham mais liberdade de movimento dentro da matriz do material. Esse aumento de desordem faz com que a entropia cres a.
Se continuarmos fornecendo energia at alcan ar a temperatura de ebuli o, as part culas come am a escapar do sistema, entrando no estado gasoso. Este o estado com maior liberdade e desordem molecular e, portanto, o de maior entropia. Quando o sistema se evapora completamente, atinge sua entropia m xima neste processo.
(ID 15246)
Se considerarmos a equa o de ERROR:5221,0 com la força mecânica ($F$) e o distância percorrida ($dx$):
| $ \Delta W = F \Delta s $ |
na sua forma de la pressão ($p$) e o volume ($V$):
| $ \delta W = p dV $ |
O trabalho desempenha o papel de um potencial, enquanto la pressão ($p$) age como uma 'for a generalizada', e o volume ($V$) serve como o caminho, uma esp cie de 'vari vel independente'. Se organizarmos esses conceitos em uma matriz para os par metros que discutimos at agora, obtemos:
| Potencial termodin mico | For a generalizada | Vari vel independente |
| Extensiva | Intensiva | Extensiva |
| $\delta W$ | $p$ | $dV$ |
| $\delta Q$ | $T$ | $?$ |
Nesse contexto, vemos que para a linha la variação de calor ($\delta Q$), temos a vari vel la temperatura absoluta ($T$), mas falta-nos uma vari vel independente extensiva. A esta chamamos de entropia e a denotamos com a letra $S$.
(ID 11183)
Existem vari veis que est o associadas a quantidades e outras que est o associadas a propriedades.• As primeiras s o chamadas de vari veis extensivas, pois podem ser estendidas ou aumentadas em propor o quantidade de subst ncia presente. Exemplos de vari veis extensivas incluem volume, massa, carga el trica, calor, entre outros.• Por outro lado, as segundas s o chamadas de vari veis intensivas, que representam propriedades que n o dependem da quantidade de subst ncia presente. Essas propriedades n o se alteram quando a quantidade de subst ncia alterada. Exemplos de vari veis intensivas incluem densidade, press o, temperatura, entre outros.
(ID 11182)
Se a entropia for estimada em fun o da temperatura, as seguintes observa es podem ser feitas:
• Em cada fase (s lido, l quido, gasoso), a entropia tende a aumentar ligeiramente com a temperatura.
• Durante as transi es de fase, ocorre um salto significativo na entropia.
Isso pode ser representado da seguinte forma:

Dessa maneira, a entropia pode ser compreendida como uma medida m dia dos graus de liberdade que um sistema possui. Enquanto em cada fase a entropia aumenta gradualmente devido libera o de alguns graus de liberdade adicionais, nas transi es de fase o aumento dram tico. Um s lido composto por m ltiplas liga es que restringem o movimento dos tomos, resultando em poucos graus de liberdade. Em um l quido, muitas liga es s o rompidas, criando novas liberdades que permitem o movimento relativo, levando a m ltiplos novos graus de liberdade. Finalmente, na transi o para a fase gasosa, todas as liga es s o perdidas e cada part cula possui seus tr s graus de liberdade. medida que a temperatura aumenta, as part culas podem rotacionar e oscilar, introduzindo novos graus de liberdade e incrementos adicionais na entropia.
(ID 11187)
Se considerarmos dois sistemas id nticos, um com uma temperatura $T_1$ e o outro com uma temperatura $T_2$, suas entropias podem ser calculadas usando a seguinte equa o envolvendo la entropia ($S$), la temperatura absoluta ($T$), la calor específico da amostra ($C$), la entropia básica ($S_0$) e la temperatura base ($T_0$):
| $ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$ |
Portanto, as entropias ser o:
$S_1 = S_0 + C\log\left(\displaystyle\frac{T_1}{T_0}\right)$
e
$S_2 = S_0 + C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Se ambos os sistemas forem misturados, sua temperatura ser a temperatura m dia:
$T_m=\displaystyle\frac{1}{2}(T_1+T_2)$
Portanto, a entropia do novo sistema ser :
$S_{1+2}=2S_0+2C\log\left(\displaystyle\frac{T_m}{T_0}\right)=2S_0+2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)$
A entropia do novo sistema maior do que a soma das entropias individuais:
$\Delta S=2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)-C\log\left(\displaystyle\frac{T_1}{T_0}\right)-C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Se representarmos graficamente $\Delta S/C$ em fun o de $T_1/T_0$ e $T_2/T_0," obtemos a seguinte figura:

$\Delta S/C$ quase nulo se as temperaturas forem muito semelhantes ($T_1\sim T_2$). No entanto, se as temperaturas forem diferentes, a entropia sempre aumentar . Se estudarmos isso em outros sistemas, observaremos que sempre que ocorre uma mudan a irrevers vel, a entropia aumenta. A mistura irrevers vel, o que significa que o sistema n o retornar ao seu estado inicial sem interven o externa. Em outras palavras, o sistema n o se separar espontaneamente em dois subsistemas com temperaturas completamente diferentes.
(ID 11186)
(ID 15305)
ID:(1471, 0)
