Usuario:
Choques entre Partículas
Storyboard 
La forma mas básica de interacción son los choques entre las partículas. Estas dependerán del tamaño de las partículas y la concentración de estas.
ID:(1496, 0)
Camino libre con concentración de moles
Ecuación
Dado que el diámetro de la partícula $d$ es el doble del radio $a$
$d=2a$
y la concentración de partículas $c_N$ se puede expresar en términos de la concentración molar $c_n$ como
$c_N=N_Ac_n$
donde $N_A$ es el número de Avogadro, la ecuación del camino libre
$l=\displaystyle\frac{1}{4a^2\pi c_N}$
también se puede expresar como:
 $l=\displaystyle\frac{1}{d^2\pi c N_A}$ |
ID:(4477, 0)
Camino libre con concentración de partículas
Ecuación
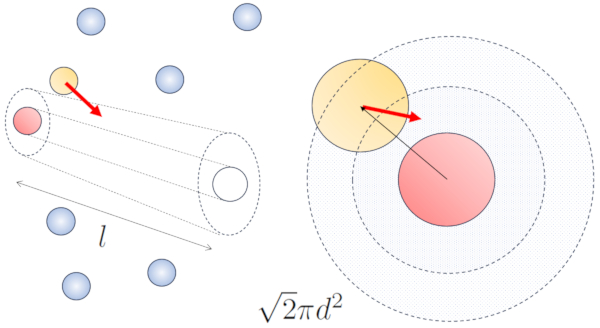
El camino libre medio se puede estimar en función del diámetro de un cilindro imaginario que rodea una partícula, teniendo en promedio una colisión con otra partícula.
El radio del cilindro corresponde a la distancia máxima que dos partículas deben tener para colisionar, lo que equivale a dos veces el radio de la partícula, es decir, el diámetro de la partícula ($d$). Dado que solo ocurre una colisión en este cilindro, el número de partículas contenidas en él debe ser igual a uno. Esto significa que:
$l d^2\pi c_n= 1$
con la concentración de particulas ($c_n$) y resolviendo para el camino libre ($\bar{l}$), obtenemos:
| $ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$ |
Esto representa el camino libre medio.
ID:(4392, 0)
Camino libre con movimiento de vecinos
Concepto
Cuando las partículas vecinas están en movimiento, existe una mayor probabilidad de colisión debido a que durante el mismo intervalo de tiempo, recorren una mayor distancia. Las componentes de velocidad, $v_x$, $v_y$, y $v_z$, fluctúan alrededor de valores medios $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ y $\sqrt{\langle v_z^2\rangle}$. Si asumimos que el sistema es isotrópico, el promedio de cada componente será igual a $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Por lo tanto, en el eje a lo largo del cual se desplaza la partícula, recorrerá una distancia
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
Al mismo tiempo, las partículas que se desplazan perpendicularmente habrán recorrido una distancia:
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Por lo tanto, la probabilidad de colisión aumentará en un factor de $\sqrt{2}$ en comparación con el caso en el que las partículas no se desplazan:
ID:(1963, 0)
Camino libre de una Molécula
Descripción
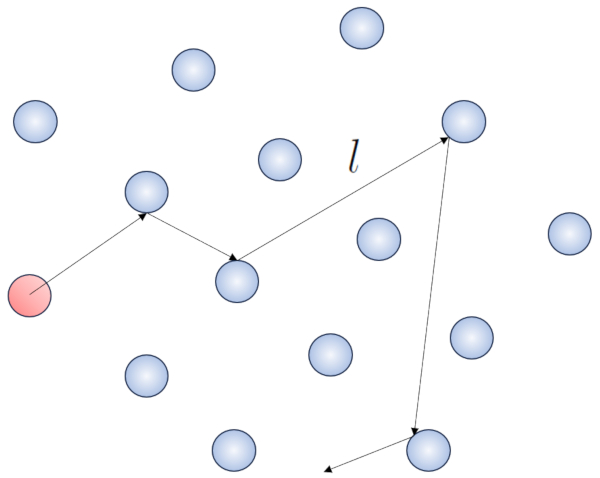
Cuando una molécula se desplaza periódicamente a través del volumen que contiene el gas, eventualmente se encontrará con otra molécula y podrán chocar. La distancia que recorre entre dos choques consecutivos se denomina 'camino libre medio'.
ID:(114, 0)
Camino libre en un gas
Concepto
Cuando una partícula de un gas se desplaza, interactúa con las demás partículas en su entorno. La forma más simple de esta interacción es a través de choques elásticos, lo que significa que la partícula choca sin perder energía, cambiando su dirección para luego impactar con otra partícula.
Dentro de este proceso, tiene sentido definir el camino libre ($\bar{l}$), cuyo valor dependerá de una concentración de particulas ($c_n$).
ID:(1708, 0)
Camino libre medio para vecinos en movimiento
Ecuación
Para el caso sin movimiento, la probabilidad es de el camino libre ($\bar{l}$), mientras que con movimiento, las probabilidades son de el diámetro de la partícula ($d$) y la concentración de particulas ($c_n$), respectivamente.
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
En el caso del movimiento, la probabilidad se incrementa en un factor de $\sqrt{2}$, lo que significa que el camino libre es
| $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)
Camino libre medio para vecinos en reposo
Ecuación
Si
$l\pi d^2c_n=1$
o
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
ID:(3942, 0)
Camino libre sin movimiento de vecinos
Concepto
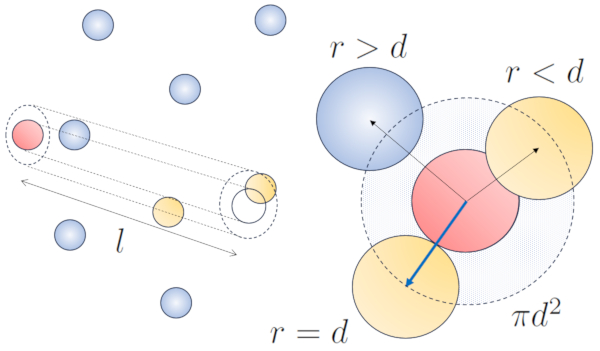
Cuando una partícula de un radio dado se desplaza en el espacio, efectivamente ocupa el espacio de un cilindro con el mismo radio. Para que esta partícula colisione con otra, esta segunda debe tener parte de su volumen dentro de dicho cilindro. En el caso más extremo, la segunda partícula se encuentra a una distancia de dos radios del primero, de manera que el borde del cilindro está en contacto con un punto de la esfera más cercano al eje del cilindro. El centro de esta esfera se encuentra a una distancia igual a un radio desde la superficie del cilindro:
Por lo tanto, la distancia entre el eje del cilindro y el centro de cualquier partícula es de dos radios, es decir, un diámetro. En otras palabras, se puede concebir que el volumen ocupado de manera literal por la partícula que se desplaza en el espacio es un cilindro con una longitud igual al camino libre y un radio igual al diámetro de la propia partícula.
ID:(1962, 0)
Concentración en base a masa molar
Ecuación
Si dividimos la densidad ($\rho$) por la masa de la partícula ($m$), obtendremos la concentración de particulas ($c_n$):
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
Dado la concentración de particulas ($c_n$) con el número de partículas ($N$) y el volumen ($V$), obtenemos:
| $ c_n \equiv \displaystyle\frac{ N }{ V }$ |
Con la masa de la partícula ($m$) y la masa ($M$),
| $ m \equiv \displaystyle\frac{ M }{ N }$ |
Como la densidad ($\rho$) es
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
obtenemos
$c_n=\displaystyle\frac{N}{V}=\displaystyle\frac{M}{mV}=\displaystyle\frac{\rho}{m}$
Por lo tanto,
| $ c_n =\displaystyle\frac{ \rho }{ m }$ |
ID:(10623, 0)
Concentración molar
Ecuación
La concentración molar ($c_m$) corresponde al número de moles ($n$) por el volumen ($V$) de un gas y se calcula como sigue:
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
ID:(4878, 0)
Concentración partículas y moles
Ecuación
Para convertir la concentración molar ($c_m$) en la concentración de particulas ($c_n$), simplemente multiplique la primera por el número de Avogadro ($N_A$), así:
| $ c_n = N_A c_m $ |
ID:(10624, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ c_m \equiv\displaystyle\frac{ n }{ V }$
c_m = n / V
$ c_n = N_A c_m $
c_n = N_A * c_m
$ c_n =\displaystyle\frac{ \rho }{ m }$
c_n = rho / m
$ l =\displaystyle\frac{1}{ d ^2 \pi c_n }$
l = 1/( d ^2 * pi * c )
$l=\displaystyle\frac{1}{d^2\pi c N_A}$
l = 1 / ( d^2 * pi * c_n * N_A )
$ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$
l = 1 / ( pi * d^2 * c_n )
$l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$
l = 1 / ( sqrt(2) * pi * d^2 * c_n )
ID:(15352, 0)