Benützer:
Modelo de Drude de un solido
Definition 
En 1904 Paul Drude propuso modelar un solido (cristal) como una grilla con átomos que interactuan de modo de formar pequeños osciladores.
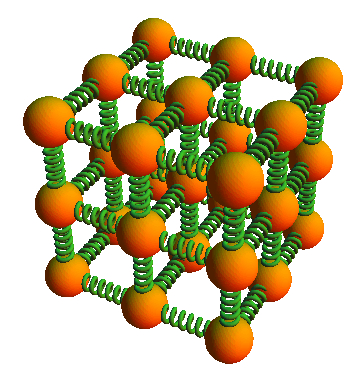
Átomos ligados con conectores tipo resortes
ID:(9507, 0)
Modelo Clásico del Solido
Storyboard
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Beispiele
En 1904 Paul Drude propuso modelar un solido (cristal) como una grilla con tomos que interactuan de modo de formar peque os osciladores.
En general las part culas pueden interactuar lo que se refleja en en energ as potenciales que dependen de dos o mas part culas, como por ejemplo
Un caso especial es cuando no existe esta interacci n y la energ a potencial solo depende de la posici n de la part cula misma y no de otras vecinas. Con
Una situaci n especial es cuando e modela la presencia de part culas vecinas v a un campo promedio. En este caso tambi n se tiene un potencial que solo depende de la posici n de la part cula aun que el potencial representa como todos los vecinos actual sobre la part cula.
Un caso especial de potencial es el caso de que este sea independiente tanto de momento como posici n asumiendo un valor constante
Un potencial part cula es el de un resorte que depende de
El modelo se puede llevar a una de cristal con potenciales tipo resortes escalando la posici n con la distancia entre los tomos del cristal
Si el potencial se define con
tiene sentido definir la frecuencia angular
que corresponde a la frecuencia angular con que oscilar a en el limite cl sico.
La funci n partici n de un sistema cl sico\\n\\n
Z=\displaystyle\frac{1}{h^{3N}N!}\int\prod_id^3p_i\prod_id^3q_ie^{-\beta E}
la energ a cin tica se puede representar por la gausseana en el momento y la interacci n por una funci n potencial
con
Se puede suponer que la funci n partici n general es con
V^N e^{-\beta V_0 N}
\\n\\ny la integral sobre la gausseana del momento es\\n\\n
\displaystyle\int_{-\infty}^{\infty}dp,e^{-\beta p^2/2m}=\sqrt{\displaystyle\frac{2\pi m}{\beta}}
y la funci n partici n es con
que corresponde a la de un gas ideal.
Podemos asumir un modelo de un solido, en que cada part cula interactua con sus vecinos v a campo efectivo con lo que se describe como que fuera con
Se puede suponer que la funci n partici n general es con
con
Podemos suponer que el potencial
\displaystyle\int_{-\infty}^{\infty}dq,e^{- \beta V_a q ^2/2 a ^2}=\sqrt{\displaystyle\frac{2 \pi a^2 }{ \beta V_a }}
\\n\\ny la integral sobre la gausseanas del momento es\\n\\n
\displaystyle\int_{-\infty}^{\infty}dp,e^{-\beta p^2/2m}=\sqrt{\displaystyle\frac{2\pi m}{\beta}}
Por ello la funci n partici n de un solido cl sico ser a de la forma con
Si se reordena la funci n partici n con
Z=\left(\displaystyle\frac{2\pi k_B T }{h}\sqrt{\displaystyle\frac{ m a ^2}{ V_a }}\right)^{3N}e^{-3 N \beta V_0 }
con lo que tiene sentido definir una temperatura caracter stica igual a con
en que se empleo la definici n de la constante de Planck
La funci n partici n con
por lo que con
se obtiene que con
Como la funci n partici n con
el logaritmo de la funci n partici n es
Como la funci n partici n con
con la definici n de
el logaritmo de la funci n partici n es con
Como la funci n partici n con
el logaritmo de la funci n partici n es
ID:(838, 0)