Loading [MathJax]/extensions/tex2jax.js
User: No user logged in.


Gaussian distribution
Storyboard

In the limit of similar probabilities the binomial distribution is reduced in the continuous limit to the Gaussean distribution.

>Model

ID:(1556, 0)


Example comparison with Gaussian distribution
Definition

If we study the binomial distribution for large numbers N and probabilities around 1/2

$P(x)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}$



which is represented below:

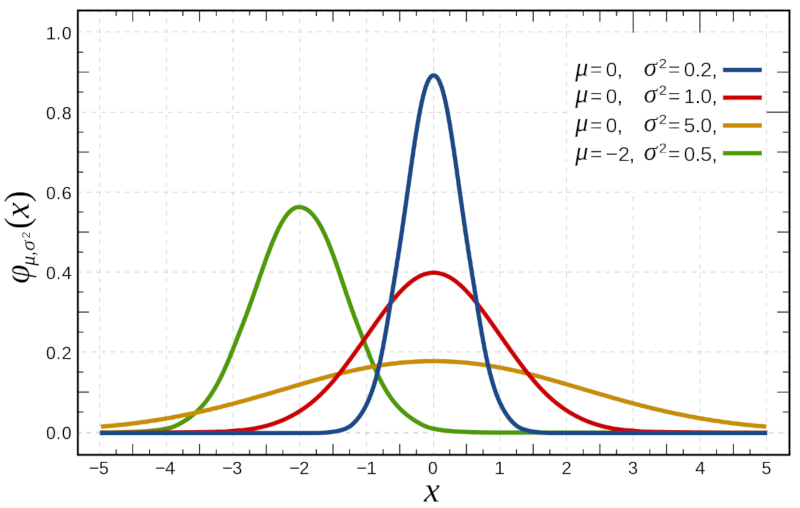
ID:(7793, 0)


Gaussian distribution
Storyboard

In the limit of similar probabilities the binomial distribution is reduced in the continuous limit to the Gaussean distribution.

Variables

Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$\sigma$
sigma
Desviación estándar de Gauss
-
$n$
n
Number
-
$q$
q
Número de pasos hacia la derecha
-
$n_1$
n_1
Número de pasos hacia la izquierda
-
$N$
N
Número total de pasos
-
$n$
n
Número totales de pasos a la izquierda
-
$u$
u
Parameter $u$
-
$s$
s
Posición camino aleatorio
m
$\mu$
mu
Posición media
m
$P_N(m)$
P_Nm
Probabilidad de $n_1$ de $N$ pasos hacia la izquierda
-
$p$
p
Probabilidad de pasos hacia la izquierda
-
$a$
a
Step size
m

Calculations


First, select the equation:   to ,  then, select the variable:   to 
W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}P(x)=1/(sqrt(2 * pi * N ^2 * p * (1 - p ))) exp(-( x - a * N * p )^2/(2* N ^2 * p * (1- p )))P(x)=1/(sqrt(2 pi sigma^2))e^(-(x-mu)^2/2sigma^2) W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))sigma ^2 = N ^2 * p *(1- p )x=(n-Np)aW_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}p(1-p)}\left(1+\displaystyle\frac{x}{aNp}\right)^{-n-1/2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)^{-N+n-1/2}N!\sim\sqrt{2\pi N}\left(\displaystyle\frac{N}{e}\right)^N( N - n )!=sqrt(2* pi *( N - n ))*( N - n )/ e )^( N - n )n!\sim\sqrt{2\pi n}\left(\displaystyle\frac{n}{e}\right)^n\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\left(1+\displaystyle\frac{x}{aNp}\right)\sim e^{x/aNp-x^2/2a^2N^2p^2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\sim e^{-x/aN(1-p)-x^2/2a^2N^2(1-p)^2}\mu=aNpu=\displaystyle\frac{x}{aNp}u=\displaystyle\frac{x}{aN(1-p)}sigmanqn_1NnusmuP_Nmpa
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used
W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}P(x)=1/(sqrt(2 * pi * N ^2 * p * (1 - p ))) exp(-( x - a * N * p )^2/(2* N ^2 * p * (1- p )))P(x)=1/(sqrt(2 pi sigma^2))e^(-(x-mu)^2/2sigma^2) W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))sigma ^2 = N ^2 * p *(1- p )x=(n-Np)aW_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}p(1-p)}\left(1+\displaystyle\frac{x}{aNp}\right)^{-n-1/2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)^{-N+n-1/2}N!\sim\sqrt{2\pi N}\left(\displaystyle\frac{N}{e}\right)^N( N - n )!=sqrt(2* pi *( N - n ))*( N - n )/ e )^( N - n )n!\sim\sqrt{2\pi n}\left(\displaystyle\frac{n}{e}\right)^n\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\left(1+\displaystyle\frac{x}{aNp}\right)\sim e^{x/aNp-x^2/2a^2N^2p^2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\sim e^{-x/aN(1-p)-x^2/2a^2N^2(1-p)^2}\mu=aNpu=\displaystyle\frac{x}{aNp}u=\displaystyle\frac{x}{aN(1-p)}sigmanqn_1NnusmuP_Nmpa


Equations

Examples

Con list=8970 la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

equation=8970



con list=3358 el n mero total de pasos es

equation=3358



y solo existe la probabilidad de ir a la derecha o a la izquierda, con list=8965 se tiene para las probabilidades que

equation=8965



por lo que con list se tiene la distribuci n binomial

equation

With the Stirling approximation

equation=8966

and the change of variables

equation=8996

you get that

equation

With the Stirling approximation

equation=8966

and the change of variables

equation=11431

you get that

equation

With the Stirling approximation

equation=8966

and the change of variables

equation=8997

the expression is

equation

In the case of medium probabilities (p \sim q \sim 1/2) and large numbers N it can be shown with

equation=8998

equation=9003

and

equation=8999

is obtained

equation

The expression

equation=8961

is reduced by

equation=507

to representation

equation

If total N steps are taken with a probability p in the right direction and these have a length a the expected final position will be

equation

To obtain the Gaussian distribution it is necessary to develop the distribution around its deviation from its mean position that can be given by

equation

As the way is

equation=8973

factor n/N can be written as

equation

As the way is

equation=8973

factor n/N can be written as

equation

If large numbers and probabilities around 1/2 are entered in the binomial distribution for the case

equation=506

the expressions

equation=9004

and

equation=9005


a distribution of the form is obtained

equation

To develop the 1+x/aNp factor you can work with the variable change

equation

With the approximation

equation=9001

it has to

equation

To develop the factor 1+x/aN(1-p) you can work with the variable change

equation

With the approximation

equation=9001

it has to

equation

It can be shown that for a large number N and probability p neither too small nor too close to 1, the binomial distribution is reduced to a gausseana for the position x=na:

equation

In this case, the probability q was replaced by 1-p.

$\begin{matrix}

P(x) & = & \displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}\\

\sigma^2 & = & Np(1-p)\\

\end{matrix}

$

The standard deviation of the binomial distribution at the limit N large and p medium is

equation

If we study the binomial distribution for large numbers N and probabilities around 1/2

equation=3368

which is represented below:

image

>Model

ID:(1556, 0)