Modelo de Drude de un solido
Image 
En 1904 Paul Drude propuso modelar un solido (cristal) como una grilla con átomos que interactuan de modo de formar pequeños osciladores.
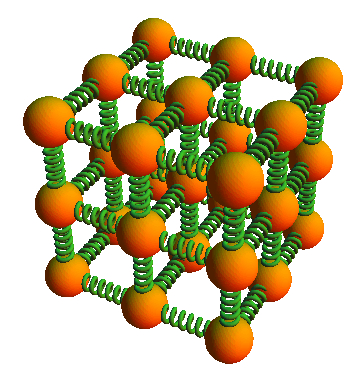
Átomos ligados con conectores tipo resortes
ID:(9507, 0)
Partículas sin interacción
Equation 
En general las partículas pueden interactuar lo que se refleja en en energías potenciales que dependen de dos o mas partículas, como por ejemplo
Un caso especial es cuando no existe esta interacción y la energía potencial solo depende de la posición de la partícula misma y no de otras vecinas. Con es
| V(q_i,q_j) = V(q_i) \delta_{ij} |
Una situación especial es cuando e modela la presencia de partículas vecinas vía un campo promedio. En este caso también se tiene un potencial que solo depende de la posición de la partícula aun que el potencial representa como todos los vecinos actual sobre la partícula.
ID:(9503, 0)
Potencial constante
Equation 
Un caso especial de potencial es el caso de que este sea independiente tanto de momento como posición asumiendo un valor constante
| V = V_0 |
ID:(9502, 0)
Potencial de un resorte
Equation 
Un potencial partícula es el de un resorte que depende de es
| V =\displaystyle\frac{1}{2} k x ^2 |
El modelo se puede llevar a una de cristal con potenciales tipo resortes escalando la posición con la distancia entre los átomos del cristal
| V(q) = V_0 + \displaystyle\frac{1}{2} V_a \left(\displaystyle\frac{ q }{ a }\right)^2 |
ID:(9504, 0)
Frecuencia propia de los osciladores
Equation 
Si el potencial se define con constante del resorte N/m, energía potencial entre partículas J, posición de la partícula m and posición del origen de la partícula m como
| V(q) = V_0 + \displaystyle\frac{1}{2} V_a \left(\displaystyle\frac{ q }{ a }\right)^2 |
tiene sentido definir la frecuencia angular
| \omega_s \equiv \sqrt{\displaystyle\frac{ V_a }{ m a ^2}} |
que corresponde a la frecuencia angular con que oscilaría en el limite clásico.
ID:(13654, 0)
Función partición en un sistema clásico
Equation 
La función partición de un sistema clásico\\n\\n
Z=\displaystyle\frac{1}{h^{3N}N!}\int\prod_id^3p_i\prod_id^3q_ie^{-\beta E}
la energía cinética se puede representar por la gausseana en el momento y la interacción por una función potencial
| Z_s =\displaystyle\frac{1}{ h ^{3 N } N !}\int\prod_i d^3 p_i \prod_i d^3 q_i e^{- \beta \sum_i( p_i ^2/2 m +V(q_i)) } |
con
ID:(7984, 0)
Función partición en la aproximación de un potencial constante
Equation 
Se puede suponer que la función partición general es con constante de Planck J s, energía potencial entre partículas J, función partición del solido clásico -, masa de la partícula kg, momento de la partícula i kg m/s, numero de partículas -, pi rad and posición de la partícula i m
| Z_s =\displaystyle\frac{1}{ h ^{3 N } N !}\int\prod_i d^3 p_i \prod_i d^3 q_i e^{- \beta \sum_i( p_i ^2/2 m +V(q_i)) } |
\\n\\ncon
V^N e^{-\beta V_0 N}
\\n\\ny la integral sobre la gausseana del momento es\\n\\n
\displaystyle\int_{-\infty}^{\infty}dp,e^{-\beta p^2/2m}=\sqrt{\displaystyle\frac{2\pi m}{\beta}}
y la función partición es con constante de Planck J s, energía potencial entre partículas J, función partición del solido clásico -, masa de la partícula kg, momento de la partícula i kg m/s, numero de partículas -, pi rad and posición de la partícula i m
| Z =\displaystyle\frac{1}{ h ^{3 N } N !}\left(\displaystyle\frac{2 \pi m }{ \beta }\right)^{3 N /2} V ^ N e^{- N \beta V_0 } |
que corresponde a la de un gas ideal.
ID:(8023, 0)
Función partición en la aproximación harmonica
Equation 
Podemos asumir un modelo de un solido, en que cada partícula interactua con sus vecinos vía campo efectivo con lo que se describe como que fuera con energía potencial entre partículas J, posición de la partícula i m and posición de la partícula j m
| V(q_i,q_j) = V(q_i) \delta_{ij} |
Se puede suponer que la función partición general es con constante de Planck J s, energía potencial entre partículas J, función partición del solido clásico -, masa de la partícula kg, momento de la partícula i kg m/s, numero de partículas -, pi rad and posición de la partícula i m
| Z_s =\displaystyle\frac{1}{ h ^{3 N } N !}\int\prod_i d^3 p_i \prod_i d^3 q_i e^{- \beta \sum_i( p_i ^2/2 m +V(q_i)) } |
con
Podemos suponer que el potencial
| V(q) = V_0 + \displaystyle\frac{1}{2} V_a \left(\displaystyle\frac{ q }{ a }\right)^2 |
\\n\\nEntonces el integral en la posición
\displaystyle\int_{-\infty}^{\infty}dq,e^{- \beta V_a q ^2/2 a ^2}=\sqrt{\displaystyle\frac{2 \pi a^2 }{ \beta V_a }}
\\n\\ny la integral sobre la gausseanas del momento es\\n\\n
\displaystyle\int_{-\infty}^{\infty}dp,e^{-\beta p^2/2m}=\sqrt{\displaystyle\frac{2\pi m}{\beta}}
Por ello la función partición de un solido clásico sería de la forma con constante de Planck J s, energía potencial entre partículas J, función partición del solido clásico -, masa de la partícula kg, momento de la partícula i kg m/s, numero de partículas -, pi rad and posición de la partícula i m
| Z =\displaystyle\frac{1}{ h ^{3 N }}\left(\displaystyle\frac{2 \pi }{\beta}\right)^{3 N }\left(\displaystyle\frac{ m a ^2}{ V_a }\right)^{3 N /2}e^{-3 N \beta V_0 } |
ID:(8024, 0)
Temperatura característica
Equation 
Si se reordena la función partición con beta 1/J, constante de Planck J s, constante del resorte N/m, energía potencial de deformación macroscopica J, función partición del solido clásico -, masa de la partícula kg, numero de partículas - and pi rad
| Z =\displaystyle\frac{1}{ h ^{3 N }}\left(\displaystyle\frac{2 \pi }{\beta}\right)^{3 N }\left(\displaystyle\frac{ m a ^2}{ V_a }\right)^{3 N /2}e^{-3 N \beta V_0 } |
\\n\\nse puede reescribir como\\n\\n
Z=\left(\displaystyle\frac{2\pi k_B T }{h}\sqrt{\displaystyle\frac{ m a ^2}{ V_a }}\right)^{3N}e^{-3 N \beta V_0 }
con lo que tiene sentido definir una temperatura característica igual a con beta 1/J, constante de Planck J s, constante del resorte N/m, energía potencial de deformación macroscopica J, función partición del solido clásico -, masa de la partícula kg, numero de partículas - and pi rad
| \Theta_s \equiv \displaystyle\frac{ \hbar }{ k_B }\sqrt{\displaystyle\frac{ V_a }{ m a ^2}} |
en que se empleo la definición de la constante de Planck
ID:(9556, 0)
Función partición del solido clásico en T
Equation 
La función partición con beta 1/J, constante de Planck J s, constante del resorte N/m, energía potencial de deformación macroscopica J, función partición del solido clásico -, masa de la partícula kg, numero de partículas - and pi rad es
| Z =\displaystyle\frac{1}{ h ^{3 N }}\left(\displaystyle\frac{2 \pi }{\beta}\right)^{3 N }\left(\displaystyle\frac{ m a ^2}{ V_a }\right)^{3 N /2}e^{-3 N \beta V_0 } |
por lo que con constante de Boltzmann J/K, constante de Planck J s, constante del resorte N/m, masa de la partícula kg, pi rad and temperatura de referencia clásica K
| \Theta_s \equiv \displaystyle\frac{ \hbar }{ k_B }\sqrt{\displaystyle\frac{ V_a }{ m a ^2}} |
se obtiene que con constante de Boltzmann J/K, constante de Planck J s, constante del resorte N/m, masa de la partícula kg, pi rad and temperatura de referencia clásica K es
| Z_s = \left(\displaystyle\frac{ T }{ \Theta_s }\right)^{3 N } e^{-3 N V_0 / k_B T } |
ID:(9557, 0)
Logaritmo de la función partición en T
Equation 
Como la función partición con
| Z_s = \left(\displaystyle\frac{ T }{ \Theta_s }\right)^{3 N } e^{-3 N V_0 / k_B T } |
el logaritmo de la función partición es
| \ln Z_s =- 3 N \ln\left(\displaystyle\frac{ \Theta_s }{ T }\right)-\displaystyle\frac{3 N V_0 }{ k_B T } |
ID:(9561, 0)
Función partición del solido clásico en \beta
Equation 
Como la función partición con
| Z_s = \left(\displaystyle\frac{ T }{ \Theta_s }\right)^{3 N } e^{-3 N V_0 / k_B T } |
con la definición de
| k_B T \equiv\displaystyle\frac{1}{ \beta } |
el logaritmo de la función partición es con
| Z_s = \displaystyle\frac{1}{( \beta k_B \Theta_s )^{3 N }} e^{-3 N \beta V_0 } |
ID:(13652, 0)
Logaritmo de la función partición en \beta
Equation 
Como la función partición con
| \ln Z_s =- 3 N \ln\left(\displaystyle\frac{ \Theta_s }{ T }\right)-\displaystyle\frac{3 N V_0 }{ k_B T } |
el logaritmo de la función partición es
| \ln Z_s =- 3 N \ln( \beta k_B \Theta_s )- 3 N \beta V_0 |
ID:(13653, 0)
0
Video
Video: Classic solid model
