Benützer:
Freie Weglänge in einem Gas
Konzept
Wenn sich ein Teilchen eines Gases bewegt, interagiert es mit anderen Teilchen. Die einfachste Form dieser Interaktion erfolgt durch elastische Stöße, was bedeutet, dass das Teilchen ohne Energieverlust kollidiert und seine Richtung ändert, um ein anderes Teilchen zu treffen.
Im Rahmen dieses Prozesses macht es Sinn, der Freier Weg ($\bar{l}$) zu definieren, dessen Wert von ($$) abhängen wird.
ID:(1708, 0)
Freie Weglänge mit Nachbarn mit Bewegung
Konzept
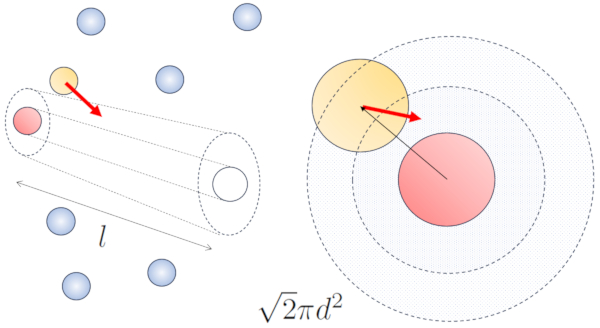
Wenn benachbarte Teilchen sich bewegen, besteht eine höhere Wahrscheinlichkeit für Kollisionen, da sie in derselben Zeitspanne eine größere Strecke zurücklegen. Die Geschwindigkeitskomponenten $v_x$, $v_y$ und $v_z$ schwanken um Mittelwerte von $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ und $\sqrt{\langle v_z^2\rangle}$. Unter der Annahme, dass das System isotrop ist, wird der Durchschnitt jeder Komponente gleich $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$ sein. Daher wird entlang der Achse, entlang der die Partikel sich bewegen, eine Strecke zurückgelegt
$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$
Zur gleichen Zeit haben Teilchen, die sich senkrecht bewegen, eine Strecke zurückgelegt:
$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$
Daher erhöht sich die Wahrscheinlichkeit einer Kollision um den Faktor $\sqrt{2}$ im Vergleich zum Fall, in dem sich die Partikel nicht bewegen:
None
ID:(1963, 0)
Mittlere Freie Weglänge für Ruhende Nachbaren
Gleichung
Wenn
$l\pi d^2c_n=1$
oder
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
ID:(3942, 0)
Freie Weglänge mit Nachbarn ohne Bewegung
Konzept
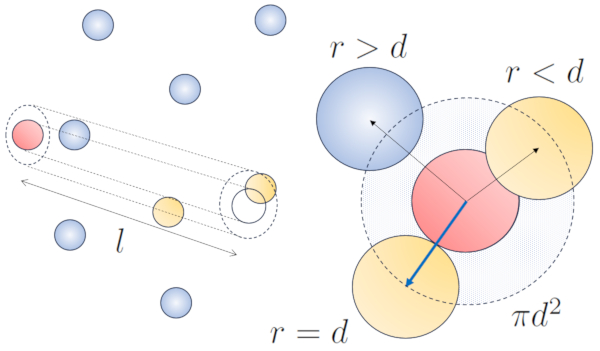
Wenn ein Teilchen mit einem gegebenen Radius sich im Raum bewegt, nimmt es effektiv den Raum eines Zylinders mit dem gleichen Radius ein. Damit ein Teilchen mit einem anderen kollidiert, muss sich dieses zweite Teilchen teilweise innerhalb dieses Zylinders befinden. Im extremsten Fall befindet sich das zweite Teilchen in einem Abstand von zwei Radien vom ersten Teilchen, so dass die Kante des Zylinders einen Punkt auf der Kugel berührt, der dem Zylinderachsen am nächsten liegt. Das Zentrum dieser Kugel ist einen Radius entfernt von der Oberfläche des Zylinders:
None
Daher beträgt der Abstand zwischen der Achse des Zylinders und dem Zentrum eines beliebigen Teilchens zwei Radien, oder anders ausgedrückt, ein Durchmesser. Im Wesentlichen kann man sich vorstellen, dass das tatsächlich vom sich durch den Raum bewegenden Teilchen eingenommene Volumen einem Zylinder mit einer Länge entspricht, die dem freien Weg entspricht, und einem Radius, der dem Durchmesser des Teilchens entspricht.
ID:(1962, 0)
Mittlere Freie Weglänge für Bewegte Nachbaren
Gleichung
Für den Fall ohne Bewegung beträgt die Wahrscheinlichkeit der Freier Weg ($\bar{l}$), während sie sich bei Bewegung auf der Partikeldurchmesser ($d$) und die Konzentration ($c_n$) ändert.
| $ l =\displaystyle\frac{1}{ \pi d ^2 c_n }$ |
Im Fall der Bewegung steigt die Wahrscheinlichkeit um den Faktor $\sqrt{2}$, was bedeutet, dass der freie Weg beträgt
 $l=\displaystyle\frac{1}{\sqrt{2}\pi d^2c_n}$ |
ID:(3943, 0)