Força de Stokes
Storyboard 
Um exemplo de força viscosa é o modelo que surge quando uma esfera se move em um meio viscoso. Esse modelo e a equação associada são conhecidos pelo nome de seu autor, George Stokes.
A força de Stokes depende da viscosidade do meio, do raio da esfera e da velocidade com que ela se move no meio. Da mesma forma, se o meio está em movimento, ele arrasta o objeto junto com ele.
ID:(1964, 0)
Força de Stokes
Storyboard 
Um exemplo de força viscosa é o modelo que surge quando uma esfera se move em um meio viscoso. Esse modelo e a equação associada são conhecidos pelo nome de seu autor, George Stokes. A força de Stokes depende da viscosidade do meio, do raio da esfera e da velocidade com que ela se move no meio. Da mesma forma, se o meio está em movimento, ele arrasta o objeto junto com ele.
Variáveis
Cálculos
Cálculos
Equações
Dado que o momento ($p$) se define con la massa inercial ($m_i$) y la velocidade ($v$),
Si la massa inercial ($m_i$) igual a la massa inicial ($m_0$), ent o podemos derivar o momento em rela o ao tempo e obter la força com massa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Portanto, chegamos conclus o de que
Se o tempo caracter stico for definido como
$\tau=\displaystyle\frac{m_i}{b}$
e o coeficiente da for a viscosa for
$b=6\pi r\eta$
Por outro lado, considerando que
e
segue-se que a massa
$m_i = \rho V = \displaystyle\frac{4\pi}{3} r^3 \rho$
o que nos leva a
$\tau = \displaystyle\frac{m_i}{b}=\displaystyle\frac{2 \rho r^2}{9\eta}$
ou seja,
Exemplos
George Stokes fez contribui es significativas nas reas de hidrodin mica e matem tica. Ele principalmente lembrado pela conhecida lei de Stokes aplicada a corpos esf ricos em um fluxo e pelo teorema de Stokes na matem tica.
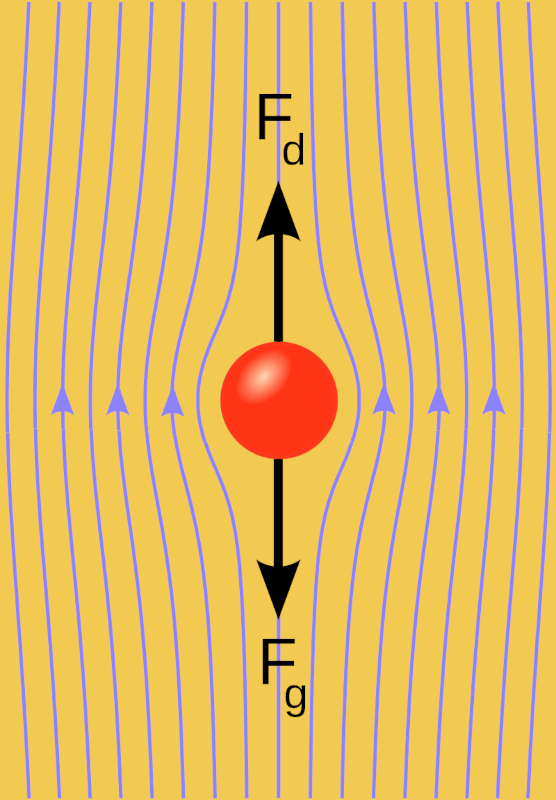
Quando uma esfera lan ada em um meio viscoso, surge uma for a inicial ascendente, uma força gravitacional ($F_g$), que afunda gradualmente o corpo. Durante esse processo, a esfera ganha velocidade, resultando em uma for a descendente, uma força viscosa ($F_v$), que depende da velocidade. Conforme a velocidade total, la força com massa constante ($F$),
come a a diminuir at se tornar nula. A partir desse momento, o movimento continua com velocidade constante, j que n o h for a para aceler -lo.
A for a de Stokes a for a gerada pelo fluxo ao redor de uma esfera de ERROR:6690,0 imersa nele. Neste caso, utiliza-se o modelo de for a proporcional a la velocidade ($v$):
Neste contexto, pode-se demonstrar que la constante de força viscosa ($b$) com la viscosidade ($\eta$) igual a:
portanto, a for a de Stokes expressa como:
Esta for a aplicada principalmente em fluxos laminares.
O movimento de uma esfera em duas dimens es caracterizado por la componente x da velocidade ($v_x$) com la velocidade horizontal inicial ($v_{0x}$), la tempo de adaptação ($\tau$) e o tempo ($t$):
e la componente y da velocidade ($v_y$) com la velocidade vertical inicial ($v_{0y}$), la tempo de adaptação ($\tau$), la aceleração gravitacional ($g$) e o tempo ($t$):
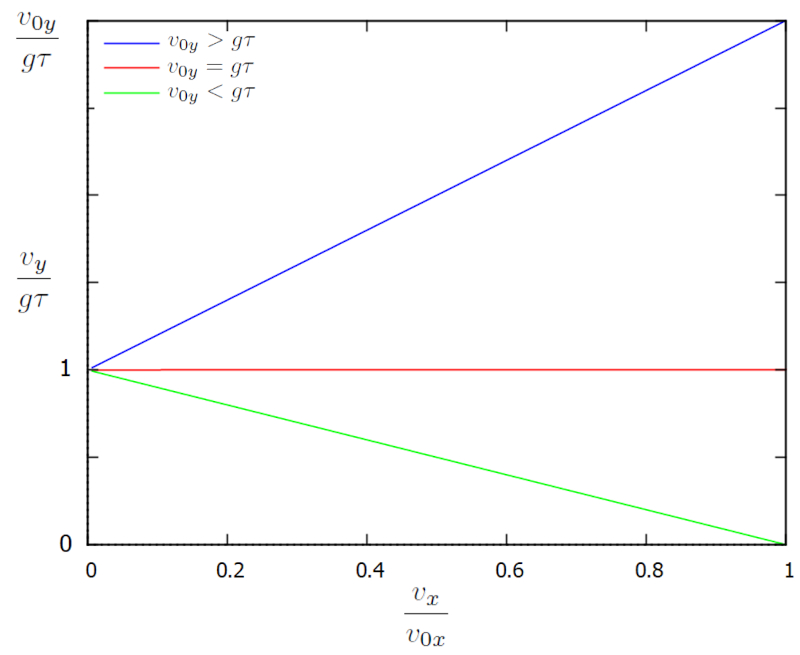
o que representado em um diagrama $v_x$ vs. $v_y$:
O diagrama mostra como ambas as componentes de velocidade evoluem ao longo do tempo. Inicialmente, $v$ igual a $v_{0x}$, o que corresponde a um ponto na borda direita do gr fico. Com o tempo, as componentes de velocidade evoluem da direita para a borda esquerda, onde a velocidade horizontal nula e a velocidade vertical atinge o limite de $g\tau$, de modo que $v/g\tau$ igual a um.
A desloca o horizontal pode ser calculada usando a equa o para la posição no eixo x ($x$) com la posição inicial no eixo x ($x_0$), la velocidade horizontal inicial ($v_{0x}$), la tempo de adaptação ($\tau$) e o tempo ($t$):
e o deslocamento vertical para la posição no eixo y ($y$) com la posição inicial no eixo y ($y_0$), la velocidade horizontal inicial ($v_{0x}$), la tempo de adaptação ($\tau$) e o tempo ($t$):
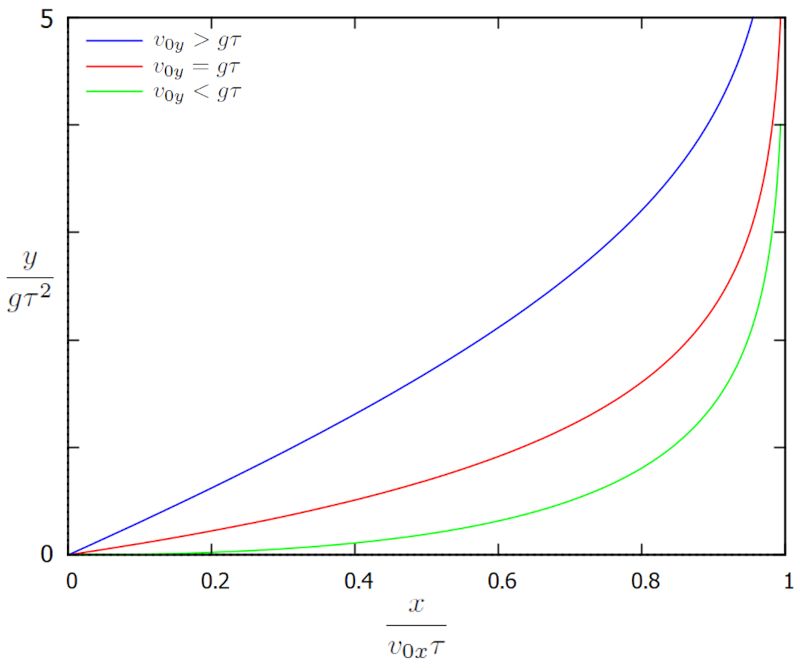
que graficamente representado nas posi es $x$ vs $y$:
Neste caso, a posi o evolui da borda esquerda para a direita, onde para o movimento horizontal alcan ando uma dist ncia m xima de $v_{0x}\tau$. O deslocamento vertical descrito com um sistema de coordenadas que tem sua origem no ponto onde a trajet ria come a e cuja vers o vertical aponta para baixo. Nesse sentido, o aumento em $y$ corresponde ao movimento descendente da esfera na dire o da gravidade.
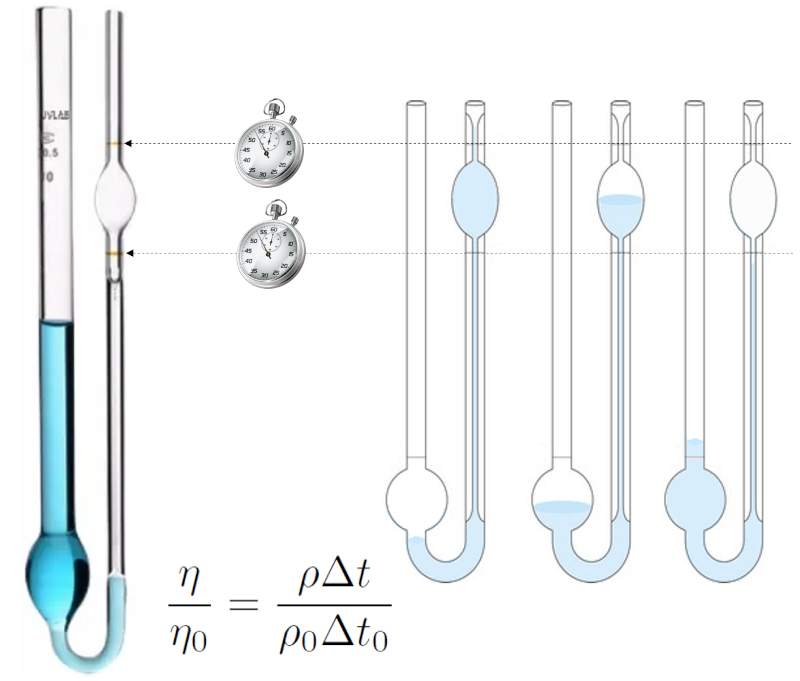
O m todo de medi o de viscosidade de Ostwald baseia-se no comportamento de um l quido fluindo atrav s de um tubo de pequeno raio (capilar).
O l quido introduzido, aplica-se suc o para exceder a marca superior e, em seguida, permite-se que escorra, medindo o tempo que leva para o n vel passar da marca superior para a inferior.
O experimento conduzido primeiro com um l quido para o qual a viscosidade e a densidade s o conhecidas (por exemplo, gua destilada), e depois com o l quido para o qual se deseja determinar a viscosidade. Se as condi es forem id nticas, o l quido fluindo em ambos os casos ser semelhante e, assim, o tempo ser proporcional densidade dividida pela viscosidade. Portanto, pode-se estabelecer uma equa o de compara o entre ambas as viscosidades:
No caso de um corpo que cai em um meio viscoso, a for a total, la força com massa constante ($F$), igual a la força gravitacional ($F_g$) menos la força viscosa ($F_v$), ent o
No caso em que la massa inercial ($m_i$) igual a la massa inicial ($m_0$),
a derivada do momento ser igual massa multiplicada pela derivada de la velocidade ($v$). Dado que a derivada da velocidade la aceleração instantânea ($a$), temos que la força com massa constante ($F$) igual a
La força gravitacional ($F_g$) baseia-se em la massa gravitacional ($m_g$) do objeto e em uma constante que reflete a intensidade da gravidade na superf cie do planeta. Esta ltima identificada por la aceleração gravitacional ($g$), que igual a $9.8 m/s^2$.
Consequentemente, conclui-se que:
A forma mais simples de la força viscosa ($F_v$) aquela que proporcional ao la velocidade ($v$) do corpo, representada por:
A constante de proporcionalidade, tamb m conhecida como la constante de força viscosa ($b$), geralmente depende da forma do objeto e da viscosidade do meio atrav s do qual ele se move. Um exemplo desse tipo de for a aquela exercida por um fluxo de fluido em um corpo esf rico, cuja express o matem tica conhecida como a lei de Stokes.
A for a de arrasto definida em fun o da viscosidade do fluido e da velocidade da esfera pela equa o:
Stokes calculou explicitamente a resist ncia sofrida pela esfera e determinou que a viscosidade proporcional ao raio da esfera e sua velocidade, resultando na seguinte equa o:
No caso da for a de Stokes em la força viscosa ($F_v$), esta modelada com la constante de força viscosa ($b$) e la velocidade ($v$),
o que corresponde a um valor de la constante de força viscosa ($b$) que, com la viscosidade ($\eta$) e ERROR:6690, igual a
La força com massa constante ($F$) igual a la força gravitacional ($F_g$) menos la força viscosa ($F_v$), ent o:
Essa rela o permite estabelecer a equa o de movimento para la aceleração instantânea ($a$) com uma massa inercial ($m_i$) caindo devido gravidade da Terra com la aceleração gravitacional ($g$), e com uma massa gravitacional ($m_g$), em la constante de força viscosa ($b$), assumir a forma de:
La volume de uma esfera ($V$) de uma esfera com um raio de uma esfera ($r$) calculado pela seguinte f rmula:
As massas que Newton utilizou em seus princ pios est o relacionadas in rcia dos corpos, o que leva ao conceito de la massa inercial ($m_i$).
A lei de Newton, que est ligada for a entre corpos devido s suas massas, est relacionada gravidade, sendo conhecida como la massa gravitacional ($m_g$).
Empiricamente, concluiu-se que ambas as massas s o equivalentes, e, portanto, definimos
Einstein foi quem questionou essa igualdade e, a partir dessa d vida, compreendeu por que ambas 'aparecem' iguais em sua teoria da gravidade. Em seu argumento, Einstein explicou que as massas deformam o espa o, e essa deforma o do espa o causa uma mudan a no comportamento dos corpos. Assim, as massas acabam sendo equivalentes. O conceito revolucion rio da curvatura do espa o implica que at mesmo a luz, que n o tem massa, afetada por corpos celestes, contradizendo a teoria da gravita o de Newton. Isso foi demonstrado experimentalmente ao estudar o comportamento da luz durante um eclipse solar. Nessa situa o, os feixes de luz s o desviados devido presen a do sol, permitindo a observa o de estrelas que est o atr s dele.
Com o modelo de Stokes, o arrasto viscoso la constante de força viscosa ($b$), que depende de ERROR:6690 e la viscosidade ambiental ($\eta$), calculado com
resulta em la tempo de viscosidade e massa inercial ($\tau_i$) e la tempo de viscosidade e massa gravitacional ($\tau_g$) assumindo valores iguais la tempo de adaptação ($\tau$), calculados com la densidade ($\rho$) atrav s de
No cen rio de movimento horizontal, a esfera enfrenta resist ncia apenas da viscosidade do meio circundante, que pode ser quantificada pela equa o envolvendo la velocidade ($v$) com la velocidade inicial ($v_0$), la tempo de viscosidade e massa inercial ($\tau_i$) e o tempo ($t$):
Consequentemente, a intera o entre esses elementos leva observa o de que la componente x da velocidade ($v_x$) com la velocidade horizontal inicial ($v_{0x}$), la tempo de adaptação ($\tau$) e o tempo ($t$):
Dentro do contexto do movimento horizontal, a posi o obtida integrando a velocidade, o que resulta em uma equa o em la posição ($s$) com la velocidade ($s_0$), la velocidade inicial ($v_0$), la tempo de viscosidade e massa gravitacional ($\tau_g$), la tempo de viscosidade e massa inercial ($\tau_i$), la aceleração gravitacional ($g$) e o tempo ($t$):
A partir desta equa o, chegamos equa o do deslocamento horizontal para la posição no eixo x ($x$) com la posição inicial no eixo x ($x_0$), la velocidade horizontal inicial ($v_{0x}$), la tempo de adaptação ($\tau$) e o tempo ($t$):
Com a equa o de movimento de um corpo em um meio viscoso, temos a derivada de la velocidade ($v$) em o tempo ($t$) com la constante de força viscosa ($b$) e la aceleração gravitacional ($g$):
Isso define la tempo de viscosidade e massa inercial ($\tau_i$) como:
No contexto do movimento vertical, a esfera enfrenta uma resist ncia dupla: de um lado, a viscosidade do meio circundante e, de outro, a gravidade que a impulsiona para baixo. Esta ltima pode ser quantificada pela equa o em la velocidade ($v$) com la velocidade inicial ($v_0$), la tempo de viscosidade e massa gravitacional ($\tau_g$), la tempo de viscosidade e massa inercial ($\tau_i$), la aceleração gravitacional ($g$) e o tempo ($t$):
Assumimos que a massa gravitacional e a massa inercial s o id nticas, ent o obtemos a fun o para la componente y da velocidade ($v_y$) com la velocidade vertical inicial ($v_{0y}$), la tempo de adaptação ($\tau$), la aceleração gravitacional ($g$) e o tempo ($t$):
Dentro do cen rio de movimento vertical, a posi o obtida pela integra o da velocidade, o que nos d uma equa o em la posição ($s$) com la velocidade ($s_0$), la velocidade inicial ($v_0$), la tempo de viscosidade e massa gravitacional ($\tau_g$), la tempo de viscosidade e massa inercial ($\tau_i$), la aceleração gravitacional ($g$) e o tempo ($t$):
A partir desta equa o, chegamos equa o de deslocamento vertical para la posição no eixo y ($y$) com la posição inicial no eixo y ($y_0$), la velocidade horizontal inicial ($v_{0x}$), la tempo de adaptação ($\tau$) e o tempo ($t$):
ID:(1964, 0)