mechanisms

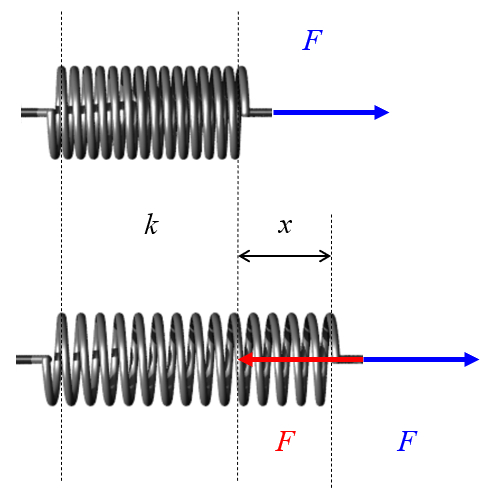
Un ressort est un fil enroul qui peut tre tir ou comprim .

image

Lorsque ces d formations sont appliqu es, le ressort g n re une force qui s'oppose au mouvement.

Si l'on mesure la force n cessaire pour obtenir une certaine d formation du ressort, on remarquera que les deux grandeurs sont proportionnelles :

image

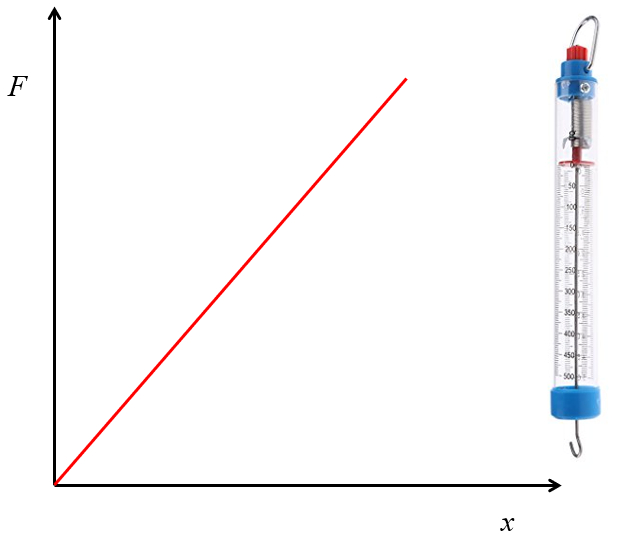
Le ressort est suspendu verticalement et des poids connus sont ajout s. La d formation r sultante est mesur e et un graphique de la force en fonction de la d formation est trac . La pente de cette relation, appel e constante lastique du ressort ou constante de Hooke, d pend des propri t s du ressort.

La lin arit de cette relation permet d'utiliser les ressorts comme m thode de mesure des forces.

La force peut tre mesur e l'aide d'un ressort, en tablissant une chelle proportionnelle la d formation qui indique directement la force associ e.

L'instrument utilis pour mesurer les forces l'aide d'un ressort est appel un dynamom tre (la 'dina' est l'unit de force dans le syst me cgs - centim tres, grammes, secondes - de telle mani re que 10^5 dinas quivalent un newton).

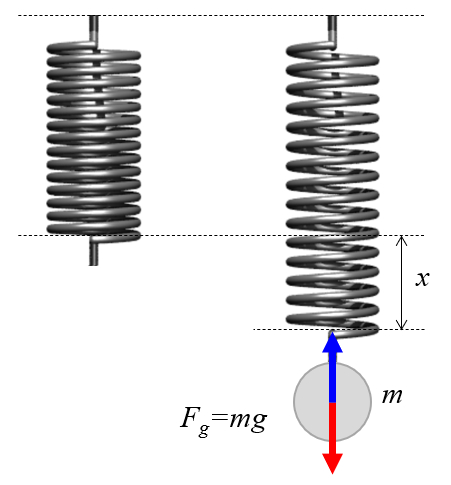
Pour tudier la fa on dont le ressort s'allonge, on peut le suspendre verticalement et ajouter progressivement des poids connus.

image

model

L' quation du mouvement est tablie avec l' quilibre des forces, ce qui signifie que a force à masse constante ($F$) est gal a force élastique ($F_k$) moins a force gravitationnelle ($F_g$):

kyon

Dans le cas o a masse d'inertie ($m_i$) est gal a masse initiale ($m_0$),

equation=12552

la d riv e de la quantit de mouvement sera gale la masse multipli e par la d riv e de a vitesse ($v$). Comme la d riv e de la vitesse est a accélération instantanée ($a$), nous avons que a force à masse constante ($F$) est gal

kyon

La relation entre a force élastique ($F_k$) et l'allongement a élongation ($u$) est exprim e et d sign e sous le nom de Loi de Hooke. La constante a constante de Hooke ($k$) est appel e la constante de raideur du ressort :

kyon

A force gravitationnelle ($F_g$) est bas sur a masse gravitationnelle ($m_g$) de l'objet et sur une constante qui refl te l'intensit de la gravit la surface de la plan te. Cette derni re est identifi e par a accélération gravitationnelle ($g$), qui est gal $9.8 m/s^2$.

Par cons quent, on en conclut que :

kyon

L' quation du mouvement est obtenue directement partir de l' quation des forces, o a force à masse constante ($F$) est gal a force élastique ($F_k$) moins a force gravitationnelle ($F_g$) :

equation=15560

Cette quation est exprim e par rapport aux diff rentes forces impliqu es, y compris a accélération instantanée ($a$), a allongement du ressort ($x$), a constante de Hooke ($k$), a masse d'inertie ($m_i$), a masse gravitationnelle ($m_g$) et a accélération gravitationnelle ($g$), comme suit :

kyon

Les masses que Newton a utilis es dans ses principes sont li es l'inertie des corps, ce qui conduit au concept de a masse d'inertie ($m_i$).

La loi de Newton, qui est li e la force entre les corps en raison de leurs masses, est associ e la gravit et est donc connue sous le nom de a masse gravitationnelle ($m_g$).

Empiriquement, on a conclu que les deux masses sont quivalentes, et donc nous d finissons

kyon

Einstein a t celui qui a remis en question cette galit et, partir de ce doute, a compris pourquoi les deux 'apparaissent' gales dans sa th orie de la gravit . Dans son argument, Einstein a expliqu que les masses d forment l'espace, et cette d formation de l'espace provoque un changement dans le comportement des corps. Ainsi, les masses s'av rent tre quivalentes. Le concept r volutionnaire de la courbure de l'espace implique m me que la lumi re, qui n'a pas de masse, est affect e par les corps c lestes, ce qui contredit la th orie de la gravitation de Newton. Cela a t d montr exp rimentalement en tudiant le comportement de la lumi re lors d'une clipse solaire. Dans cette situation, les faisceaux lumineux sont d vi s en raison de la pr sence du soleil, permettant l'observation des toiles qui se trouvent derri re lui.

Le produit de a constante de Hooke ($k$) et a masse d'inertie ($m_i$) est appel a fréquence angulaire du ressort ($\omega$) et est d fini comme suit :

kyon

A fréquence angulaire ($\omega$) est avec a période ($T$) gal

kyon

La relation entre a fréquence angulaire ($\omega$) et a fréquence du son ($\nu$) sexprime comme :

kyon

A fréquence du son ($\nu$) correspond au nombre de fois qu'une oscillation se produit en une seconde. A période ($T$) repr sente le temps n cessaire une seule oscillation. Par cons quent, le nombre d'oscillations par seconde est :

kyon

La fr quence est indiqu e en Hertz (Hz).

La variable a amplitude d\'oscillation ($x$) volue selon le temps ($t$) selon l' quation de mouvement avec a fréquence angulaire de l'oscillateur ($\omega_0$) et a accélération gravitationnelle ($g$) donn e par :

equation=15561

En supposant que a amplitude initiale de l'oscillation ($x_0$) et a vitesse initiale de l'oscillateur ($v_0$) sont la solution, on peut crire :

kyon

Pour obtenir a vitesse de l\'oscillateur ($v$), il suffit de d river a amplitude d\'oscillation ($x$) par rapport le temps ($t$) :

quation=3153

Ainsi, on obtient avec a amplitude initiale de l'oscillation ($x_0$), a vitesse initiale ($v_0$) et a fréquence angulaire de l'oscillateur ($\omega_0$) que :

kyon