Zentrifugal- und Zentripetalbeschleunigung
Storyboard 
Ein Objekt mit Geschwindigkeit neigt dazu, sich geradlinig zu bewegen. Um eine kreisförmige Umlaufbahn zu verfolgen, muss ein Objekt "radikal" von seinem geraden Pfad zur Umlaufbahnradius abweichen. Dieser "Abfall" entspricht einer Zentripetalbeschleunigung (centri = Zentrum, petal = zum), wie sie von einem externen Beobachter des Systems wahrgenommen wird.
Andererseits, wenn das Objekt seinen geraden Pfad weiterverfolgt anstatt der kreisförmigen Umlaufbahn zu folgen, würde ein Beobachter im rotierenden System dieselbe Beschleunigung wahrnehmen, jedoch sich vom Zentrum entfernen. Dies wird als Zentrifugalbeschleunigung (centri = Zentrum, fuga = sich entfernend) bezeichnet.
ID:(758, 0)
Tangentialgeschwindigkeit
Bild 
Wenn ein Objekt einem Modus unterworfen wird, um einen konstanten Radius beizubehalten, wird es sich wie in der Abbildung dargestellt drehen. Bei Betrachtung der Abbildung würde man bemerken, dass die Masse eine translatorische Bewegung mit einer tangentialen Geschwindigkeit ausführt, die dem Radius mal der Winkelgeschwindigkeit entspricht:
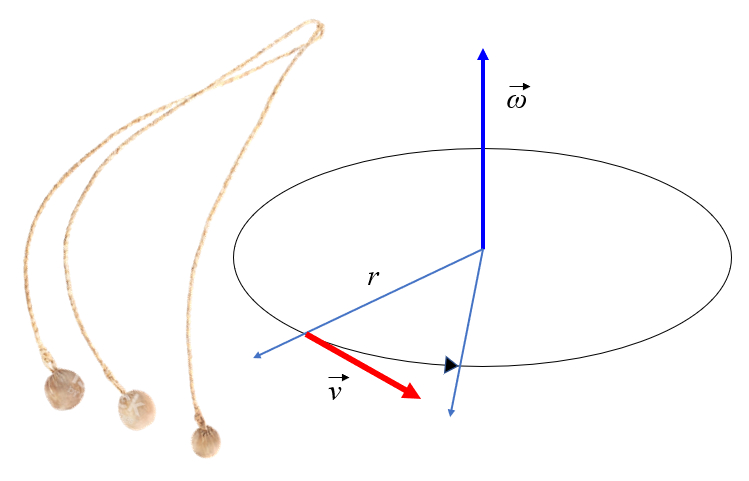
Wenn jedoch das Element, das das Objekt mit der Achse verbindet, abgeschnitten wird, wird sich das Objekt weiterhin tangential in einer geraden Linie bewegen.
ID:(310, 0)
Zentrifugal- und Zentripetalbeschleunigung
Beschreibung 
Ein Objekt mit Geschwindigkeit neigt dazu, sich geradlinig zu bewegen. Um eine kreisförmige Umlaufbahn zu verfolgen, muss ein Objekt "radikal" von seinem geraden Pfad zur Umlaufbahnradius abweichen. Dieser "Abfall" entspricht einer Zentripetalbeschleunigung (centri = Zentrum, petal = zum), wie sie von einem externen Beobachter des Systems wahrgenommen wird. Andererseits, wenn das Objekt seinen geraden Pfad weiterverfolgt anstatt der kreisförmigen Umlaufbahn zu folgen, würde ein Beobachter im rotierenden System dieselbe Beschleunigung wahrnehmen, jedoch sich vom Zentrum entfernen. Dies wird als Zentrifugalbeschleunigung (centri = Zentrum, fuga = sich entfernend) bezeichnet.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
| $ \bar{\omega} = \omega_0 $ |
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
| $ \Delta t \equiv t - t_0 $ |
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
| $ \Delta s = s - s_0 $ |
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Die Gleichung f r die durchschnittliche Geschwindigkeit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
| $ \Delta s=r \Delta\theta $ |
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
| $ v = r \omega $ |
f hrt.
(ID 3233)
(ID 3324)
(ID 3324)
(ID 3324)
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
| $ \Delta\theta = \theta_2 - \theta_1 $ |
und der Abgelaufene Zeit ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Da die Zentrifugalbeschleunigung gleich
| $ a_c =\displaystyle\frac{ v_0 ^2}{ r }$ |
mit
| $ v_0 = r \omega_0 $ |
k nnen wir folgern, dass:
| $ a_c = r \omega ^2$ |
(ID 4384)
Wenn die zur ckgelegte Strecke klein ist ($v\Delta t\ll r$), kann die Wurzel des Abstands zwischen dem Zentrum und dem K rper,
$\sqrt{r^2+(v\Delta t)^2}$
,
gen hert werden durch
$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
,
was einer Parabel in Abh ngigkeit von der Zeit $\Delta t$ entspricht. Daher kann das Verhalten mit einer Beschleunigung beschrieben werden, die wie folgt lautet:
| $ a_c =\displaystyle\frac{ v ^2}{ r }$ |
(ID 4735)
(ID 10276)
Beispiele
(ID 15417)
Wenn ein Objekt einem Modus unterworfen wird, um einen konstanten Radius beizubehalten, wird es sich wie in der Abbildung dargestellt drehen. Bei Betrachtung der Abbildung w rde man bemerken, dass die Masse eine translatorische Bewegung mit einer tangentialen Geschwindigkeit ausf hrt, die dem Radius mal der Winkelgeschwindigkeit entspricht:

Wenn jedoch das Element, das das Objekt mit der Achse verbindet, abgeschnitten wird, wird sich das Objekt weiterhin tangential in einer geraden Linie bewegen.
(ID 310)
Wenn ein K rper, der an einem Seil der L nge $r$ befestigt ist, mit einer Tangentialgeschwindigkeit $v$ rotiert und das Seil durchtrennt wird, wird der K rper aufgrund der Tr gheit mit konstanter Geschwindigkeit $v$ in einer geraden Linie weiterbewegt.

Die Umlaufbahn von Radio
In einem Zeitintervall $\Delta t$ wird der K rper eine Strecke von $v\Delta t$ tangential zu seiner vorherigen Bahn zur cklegen. Aus der Perspektive eines Beobachters auf der Achse des rotierenden Systems wird die Strecke mithilfe des Satzes des Pythagoras berechnet, indem das Quadrat des Bahnradius mit dem Quadrat der zur ckgelegten Strecke addiert wird:
$\sqrt{r^2+v^2\Delta t^2}$
(ID 1155)
Wenn wir eine Katapult betrachten, werden wir feststellen, dass das Projektil zun chst entlang der Kurve fliegt, die durch den L ffel beschrieben wird. Dies geschieht, weil der L ffel daf r konzipiert ist, das Projektil zur ckzuhalten. Sobald der Arm stoppt, bewegt sich das Projektil weiterhin in einer geraden Linie, die tangential zum Kreis verl uft, dem es zuvor gefolgt ist.
Wenn ein Objekt nicht zur ckgehalten wird und sich mit einer tangentialen Geschwindigkeit $v$ bewegt, legt es in einem Zeitintervall $\Delta t$ eine Strecke von $v\Delta t$ zur ck, indem es sich von Punkt B nach Punkt C bewegt. Wenn es jedoch weiterhin eine Umlaufbahn beibeh lt, erreicht es nach dem Zeitintervall $\Delta t$ den Punkt D. Wenn das Objekt den Punkt C erreicht, gibt es aus der Perspektive eines Beobachters auf der Erde eine Beschleunigung, die bewirkt, dass sich das Objekt von der Erde entfernt (Zentrifugalbeschleunigung) und dabei die Strecke $\Delta r$ im Zeitintervall $\Delta t$ zur cklegt.
F r einen Beobachter im Weltraum f llt ein Objekt in einer Umlaufbahn st ndig: Anstatt den Punkt C zu erreichen, f llt es im Zeitintervall $\Delta t$ ber die Strecke $\Delta r$ bis es den Punkt D erreicht. In beiden F llen k nnen wir die Situation graphisch darstellen und unter Verwendung des Satzes des Pythagoras feststellen, dass folgende Gleichung gelten muss:
$(r+\Delta r)^2=r^2+(v\Delta t)^2$
Durch Aufl sen der Gleichung ergibt sich:
$2\Delta rr+\Delta r^2=v^2\Delta t^2$
Da die Variation des Radius $\Delta r$ viel kleiner ist als der Radius selbst ($r\ll\Delta r$), k nnen wir schlussfolgern, dass gilt:
$2\Delta rr=v^2\Delta t^2$
Wenn wir nach $\Delta r$ aufl sen, erhalten wir:
$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
Wenn wir diese Gleichung mit der Gleichung $s=at^2/2$ vergleichen, k nnen wir feststellen, dass das Objekt mit einer Beschleunigung von $v^2/r$ beschleunigt.
(ID 313)
(ID 15428)
ID:(758, 0)
