Usuario:


Aceleración centrifuga y centripeta
Storyboard

Todo objeto con velocidad tiende a desplazarse en línea recta. Para que un objeto pueda seguir una órbita circular, necesita "caer" radicalmente desde su trayectoria rectilínea hasta el radio de la órbita. Esta "caída" corresponde a una aceleración centrípeta, que es hacia el centro y es lo que percibiría un observador externo al sistema.

Por otro lado, si el objeto continúa en su trayectoria rectilínea en lugar de seguir la órbita circular, un observador dentro del sistema en rotación percibirá una aceleración similar, pero alejándose del centro, lo que se conoce como aceleración centrífuga (centri = centro, fuga = alejándose).

>Modelo

ID:(758, 0)


Velocidad tangencial
Imagen

Si un objeto se somete a un modo de mantener un radio constante, girará como se indica en la figura. Al observar la figura, se notará que la masa realiza un movimiento de traslación con una velocidad tangencial que es igual al radio por la velocidad angular:

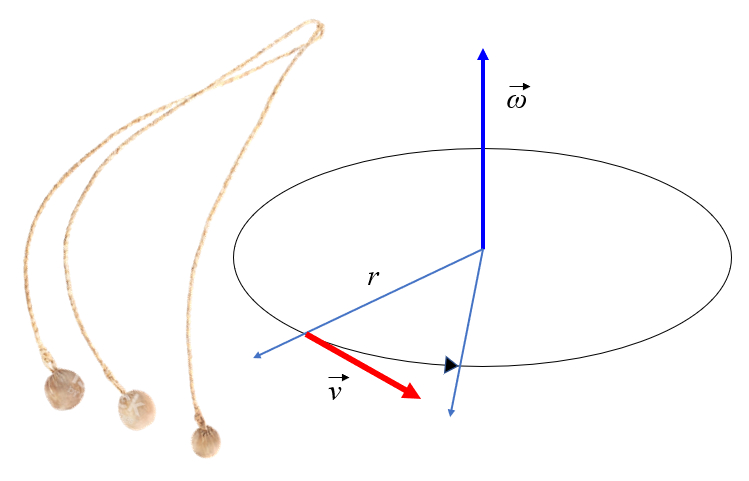
Sin embargo, si se corta el elemento que une el objeto al eje, este continuará moviéndose tangencialmente en línea recta.

ID:(310, 0)


Aceleración centrifuga y centripeta
Descripción

Todo objeto con velocidad tiende a desplazarse en línea recta. Para que un objeto pueda seguir una órbita circular, necesita "caer" radicalmente desde su trayectoria rectilínea hasta el radio de la órbita. Esta "caída" corresponde a una aceleración centrípeta, que es hacia el centro y es lo que percibiría un observador externo al sistema. Por otro lado, si el objeto continúa en su trayectoria rectilínea en lugar de seguir la órbita circular, un observador dentro del sistema en rotación percibirá una aceleración similar, pero alejándose del centro, lo que se conoce como aceleración centrífuga (centri = centro, fuga = alejándose).

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$a_c$
a_c
Aceleración centrifuga
m/s^2
$a_p$
a_p
Aceleración centripeta
m/s^2
$\theta$
theta
Ángulo
rad
$\theta_0$
theta_0
Ángulo inicial
rad
$\Delta\theta$
Dtheta
Diferencia de ángulos
rad
$\Delta s$
Ds
Distancia recorrida en un tiempo
m
$s$
s
Posición
m
$s_0$
s_0
Posición inicial
m
$r$
r
Radio
m
$t$
t
Tiempo
s
$t_0$
t_0
Tiempo inicial
s
$\Delta t$
Dt
Tiempo transcurrido
s
$\omega_0$
omega_0
Velocidad angular inicial
rad/s
$\bar{\omega}$
omega_m
Velocidad angular media
rad/s
$v_0$
v_0
Velocidad constante
m/s
$\bar{v}$
v_m
Velocidad media
m/s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),

$ \bar{\omega} = \omega_0 $



Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:

$ \Delta\theta = \theta_2 - \theta_1 $



Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:

$ \Delta t \equiv t - t_0 $



Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:

$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$



Esto se puede expresar como:

$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$



Despejando, obtenemos:

$ \theta = \theta_0 + \omega_0 ( t - t_0 )$

(ID 1023)

Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):

$ \Delta s = s - s_0 $



y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):

$ \Delta t \equiv t - t_0 $



Se tiene que la ecuaci n de la velocidad media:

$ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$



puede escribirse como:

$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$




Por lo tanto, despejando, se obtiene:

$ s = s_0 + v_0 ( t - t_0 )$

(ID 3154)

Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a

$ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$



y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un c rculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son

$ \Delta s=r \Delta\theta $



y la definici n de la velocidad angular media ($\bar{\omega}$) es

$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$



entonces,

$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$



Como la relaci n es general, se puede aplicar para valores instant neos, lo que resulta en

$ v = r \omega $

.

(ID 3233)

La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),

$ \Delta\theta = \theta_2 - \theta_1 $



y el tiempo transcurrido ($\Delta t$),

$ \Delta t \equiv t - t_0 $



La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):

$ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

(ID 3679)

Si se parte de la posición inicial ($s_0$) y se desea calcular la distancia recorrida en un tiempo ($\Delta s$), es necesario definir un valor para la posición ($s$).

En un sistema unidimensional, la distancia recorrida en un tiempo ($\Delta s$) se obtiene simplemente restando la posición inicial ($s_0$) de la posición ($s$), lo que da como resultado:

$ \Delta s = s - s_0 $

(ID 4352)

Al ser la aceleraci n centr fuga igual a

$ a_c =\displaystyle\frac{ v_0 ^2}{ r }$



con v como la velocidad y r como el radio, y considerando la relaci n entre velocidad tangencial y velocidad angular como

$ v_0 = r \omega_0 $



podemos concluir que:

$ a_c = r \omega ^2$

(ID 4384)

Si la distancia recorrida es peque a ($v\Delta t\ll r$), la ra z cuadrada de la distancia entre el centro y el cuerpo,

$\sqrt{r^2+(v\Delta t)^2}$



puede aproximarse como

$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$



lo cual corresponde a una par bola en funci n del tiempo $\Delta t$. Por lo tanto, el comportamiento puede describirse con una aceleraci n igual a:

$ a_c =\displaystyle\frac{ v ^2}{ r }$

(ID 4735)

Ejemplos


(ID 15417)

Si un objeto se somete a un modo de mantener un radio constante, girar como se indica en la figura. Al observar la figura, se notar que la masa realiza un movimiento de traslaci n con una velocidad tangencial que es igual al radio por la velocidad angular:

Sin embargo, si se corta el elemento que une el objeto al eje, este continuar movi ndose tangencialmente en l nea recta.

(ID 310)

Si un cuerpo atado a una cuerda de longitud $r$ gira con una velocidad tangencial $v$ y la cuerda es cortada, el cuerpo continuar movi ndose inercialmente en l nea recta con velocidad constante $v$.

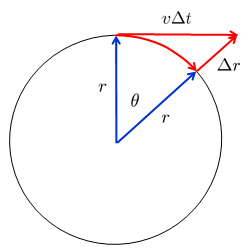
rbita circula de radio r y camino recorrido v\,dt en caso de que el objeto no es retenido. Ambas distancias representan los catetos de un rect ngulo de hipotenusa de largo igual al radio r y la distancia radial x recorrida. Aplicando Pit goras se puede asi estimar dicho camino x en funci n del tiempo t.



En un intervalo de tiempo $\Delta t$, el cuerpo habr recorrido la distancia $v\Delta t$ tangencialmente a su rbita anterior. Desde el punto de vista de un observador en el eje del sistema de rotaci n, la distancia se calcula utilizando el teorema de Pit goras, sumando el cuadrado del radio de la rbita con el cuadrado de la distancia recorrida:

$\sqrt{r^2+v^2\Delta t^2}$

(ID 1155)

Si estudiamos una catapulta, notaremos que la bala primero se mueve a lo largo de la curva que describe la cuchara. Esto sucede porque la cuchara est dise ada para retener la bala. Una vez que se detiene el brazo, la bala contin a en l nea recta en forma tangencial al c rculo que recorr a.

Si un cuerpo no est retenido y viaja con una velocidad tangencial $v$, recorrer en un tiempo $\Delta t$ la distancia $v\Delta t$, viajando desde el punto B hasta el punto C. Sin embargo, si contin a orbitando, despu s del tiempo $\Delta t$ llegar al punto D. Si el objeto llega al punto C, desde la perspectiva de un observador en la Tierra, existir una aceleraci n que hace que el objeto se aleje de la Tierra (aceleraci n centr fuga), recorriendo en el tiempo $\Delta t$ la distancia $\Delta r$.

Para un observador en el espacio, un objeto en rbita se encuentra en una ca da constante: en lugar de terminar en el punto C, cae en el tiempo $\Delta t$ la distancia $\Delta r$ hasta llegar al punto D. En ambos casos, podemos representar la situaci n y utilizando el teorema de Pit goras, podemos ver que se debe cumplir la siguiente ecuaci n:

$(r+\Delta r)^2=r^2+(v\Delta t)^2$



Si desarrollamos el cuadrado de la ecuaci n, se reduce a:

$2\Delta rr+\Delta r^2=v^2\Delta t^2$



Como la variaci n del radio $\Delta r$ es mucho m s peque a que el radio en s ($r\ll\Delta r$), podemos concluir que:

$2\Delta rr=v^2\Delta t^2$



o despejando $\Delta r$:

$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$

Comparando esta ecuaci n con la ecuaci n $s=at^2/2$, se concluye que el cuerpo acelera con una aceleraci n igual a $v^2/r$.

(ID 313)


(ID 15428)

ID:(758, 0)