Konstante Winkelgeschwindigkeit, zweistufig
Storyboard 
Wenn während einer Bewegung mit konstanter Winkelgeschwindigkeit eine Änderung dieser Geschwindigkeit auftritt, resultiert dies in einer Bewegung, die in zwei Stufen erfolgt, wobei jede durch eine definierte Winkelgeschwindigkeit gekennzeichnet ist.
Jede Stufe wird mit einer linearen Beziehung modelliert, die durch eine Linie dargestellt wird, wobei der Schlüssel darin liegt, dass die Zeit und der endgültige Winkel der ersten Stufe wiederum die Zeit und den Anfangswinkel der zweiten Stufe sind.
Es ist wichtig zu beachten, dass dieses Modell ein Problem aufweist: Die Winkelgeschwindigkeit ändert sich augenblicklich, was einer Winkelbeschleunigung gefolgt von einer unendlichen Verzögerung entspricht, was unrealistisch ist. Dieses Problem ist jedoch nicht relevant, wenn die Dauer der Stufen deutlich länger ist als die Zeit, in der die Änderung der Winkelgeschwindigkeit auftritt.
ID:(1410, 0)
Winkel und Zeiten in zwei Stufen
Zitat 
Im Fall einer Bewegung in zwei Etappen kann die erste Etappe durch eine Funktion beschrieben werden, die die Punkte der Startzeit ($t_0$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$), der Anfangswinkel ($\theta_0$) und der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$) einschließt, dargestellt durch eine Gerade mit einer Steigung von die Winkelgeschwindigkeit der ersten Stufe ($\omega_1$):
| $ \theta_1 = \theta_0 + \omega_1 ( t_1 - t_0 )$ |
Für die zweite Etappe, definiert durch die Punkte der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$), die Endwinkel der zweiten Stufe ($\theta_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$), wird eine zweite Gerade mit einer Steigung von die Winkelgeschwindigkeit der zweiten Stufe ($\omega_2$) verwendet:
| $ \theta_2 = \theta_1 + \omega_2 ( t_2 - t_1 )$ |
die wie folgt dargestellt wird:
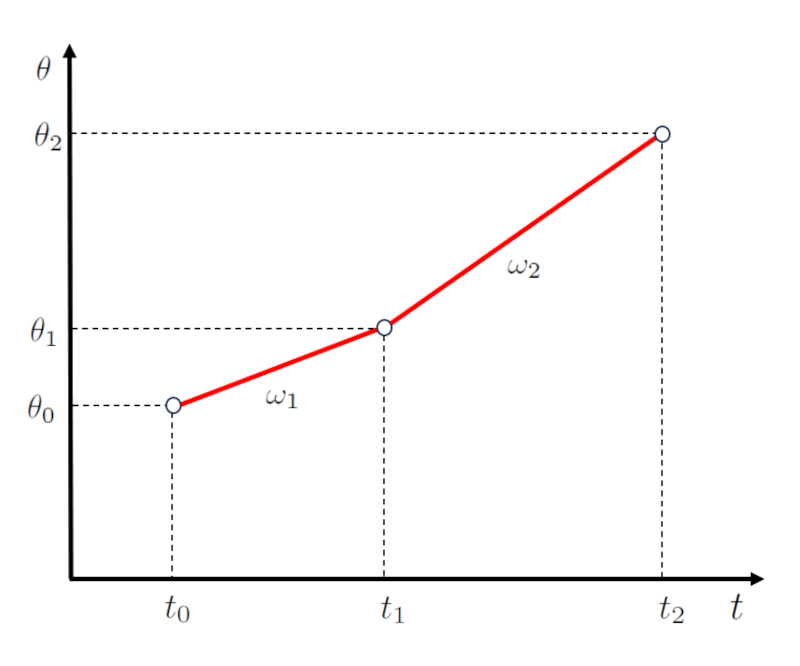
Es ist wichtig zu beachten, dass der Beginn der zweiten Etappe, definiert durch die Punkte der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$), mit dem Ende der ersten Etappe zusammenfällt.
ID:(12517, 0)
Konstante Winkelgeschwindigkeit, zweistufig
Beschreibung 
Wenn während einer Bewegung mit konstanter Winkelgeschwindigkeit eine Änderung dieser Geschwindigkeit auftritt, resultiert dies in einer Bewegung, die in zwei Stufen erfolgt, wobei jede durch eine definierte Winkelgeschwindigkeit gekennzeichnet ist.
Jede Stufe wird mit einer linearen Beziehung modelliert, die durch eine Linie dargestellt wird, wobei der Schlüssel darin liegt, dass die Zeit und der endgültige Winkel der ersten Stufe wiederum die Zeit und den Anfangswinkel der zweiten Stufe sind.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
| $ \bar{\omega} = \omega_0 $ |
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
| $ \Delta t \equiv t - t_0 $ |
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
| $ \bar{\omega} = \omega_0 $ |
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
| $ \Delta t \equiv t - t_0 $ |
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
| $ \Delta s=r \Delta\theta $ |
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
| $ v = r \omega $ |
f hrt.
(ID 3233)
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
| $ \Delta s=r \Delta\theta $ |
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
| $ v = r \omega $ |
f hrt.
(ID 3233)
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
| $ \Delta\theta = \theta_2 - \theta_1 $ |
und der Abgelaufene Zeit ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
| $ \Delta\theta = \theta_2 - \theta_1 $ |
und der Abgelaufene Zeit ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Beispiele
(ID 15410)
Ein K rper kann sich zu die Winkelgeschwindigkeit der ersten Stufe ($\omega_1$) bewegen und dann zu einer die Winkelgeschwindigkeit der zweiten Stufe ($\omega_2$) bergehen. Dies markiert den Beginn einer neuen Phase, und es ist notwendig, beide mathematisch zu beschreiben, um ihre Bewegung vorherzusagen.
Der Schl ssel ist zu beachten, dass beide Phasen einen gemeinsamen Punkt haben, der durch Folgendes gekennzeichnet ist:
• Der Endwinkel der ersten Phase und der Anfangswinkel der zweiten Phase, der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$).
• Die Endzeit der ersten Phase und der Anfangszeit der zweiten Phase, der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$).
Damit k nnen die Diagramme des Winkels ber die Zeit wie in der folgenden Darstellung gekoppelt werden:
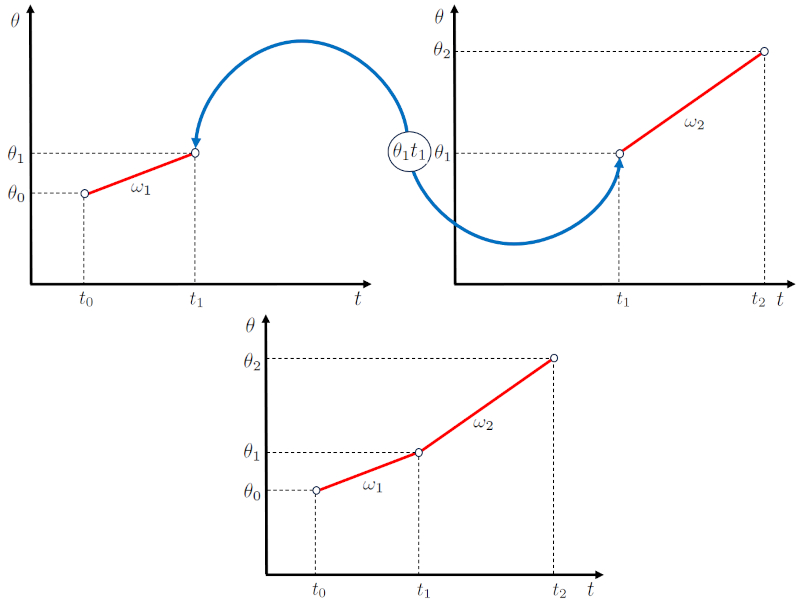
Darin gibt es einen Anfangspunkt der ersten Etappe, gekennzeichnet durch der Anfangswinkel ($\theta_0$) und der Startzeit ($t_0$), und einen Endpunkt der zweiten Etappe, gekennzeichnet durch die Endwinkel der zweiten Stufe ($\theta_2$) und der Endzeit der zweiten Etappe ($t_2$).
(ID 12518)
In einem Szenario mit zweistufiger Bewegung bewegt sich das Objekt zuerst um ein Angle reiste in der ersten Etappe ($\Delta\theta_1$) w hrend ein In der ersten Phase verstrichene Zeit ($\Delta t_1$) mit eine Winkelgeschwindigkeit der ersten Stufe ($\omega_1$).
| $ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$ |
Dann, in der zweiten Stufe, bewegt es sich um ein Angle reiste in der zweiten Etappe ($\Delta\theta_2$) w hrend ein In der zweiten Phase verbrachte Zeit ($\Delta t_2$) mit eine Winkelgeschwindigkeit der zweiten Stufe ($\omega_2$).
| $ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$ |
Wenn wir dies grafisch darstellen, erhalten wir ein Diagramm von Winkel und Zeit wie unten gezeigt:
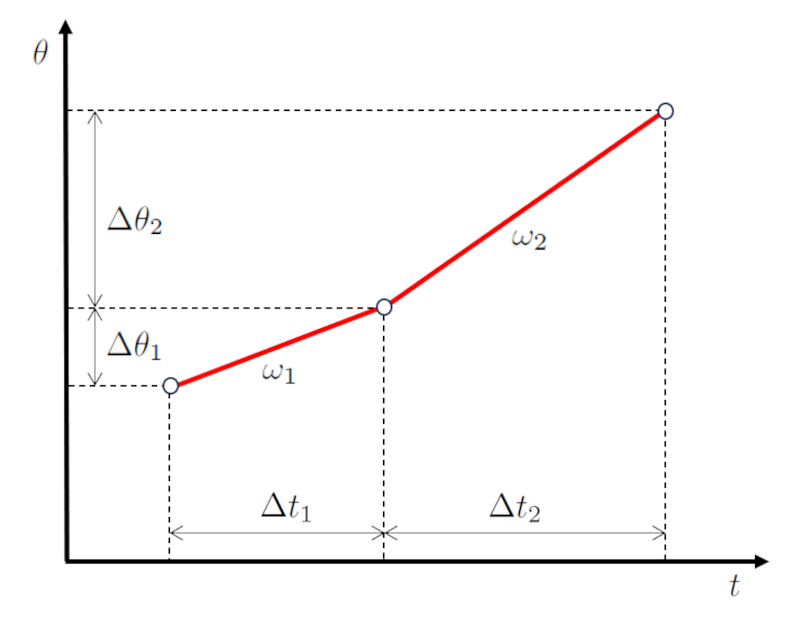
Der Schl ssel hierbei ist, dass die Werte der In der ersten Phase verstrichene Zeit ($\Delta t_1$) und der In der zweiten Phase verbrachte Zeit ($\Delta t_2$) sequentiell sind, ebenso wie die Werte der Angle reiste in der ersten Etappe ($\Delta\theta_1$) und der Angle reiste in der zweiten Etappe ($\Delta\theta_2$).
(ID 12525)
Im Fall einer Bewegung in zwei Etappen kann die erste Etappe durch eine Funktion beschrieben werden, die die Punkte der Startzeit ($t_0$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$), der Anfangswinkel ($\theta_0$) und der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$) einschlie t, dargestellt durch eine Gerade mit einer Steigung von die Winkelgeschwindigkeit der ersten Stufe ($\omega_1$):
| $ \theta_1 = \theta_0 + \omega_1 ( t_1 - t_0 )$ |
F r die zweite Etappe, definiert durch die Punkte der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$), die Endwinkel der zweiten Stufe ($\theta_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$), wird eine zweite Gerade mit einer Steigung von die Winkelgeschwindigkeit der zweiten Stufe ($\omega_2$) verwendet:
| $ \theta_2 = \theta_1 + \omega_2 ( t_2 - t_1 )$ |
die wie folgt dargestellt wird:

Es ist wichtig zu beachten, dass der Beginn der zweiten Etappe, definiert durch die Punkte der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Der erste Schlusswinkel und die zweite Etappe begannen ($\theta_1$), mit dem Ende der ersten Etappe zusammenf llt.
(ID 12517)
(ID 15421)
ID:(1410, 0)
