Storyboard

Lorsque les éléments hydrauliques sont connectés en série, le débit reste constant, mais chaque élément hydraulique subit une perte de pression. La somme de ces pertes de pression équivaut à la perte totale, et donc, la résistance hydraulique totale est égale à la somme de toutes les résistances hydrauliques individuelles. En revanche, l'inverse de la conductivité hydraulique totale est égal à la somme des inverses des conductivités hydrauliques.

>Modèle

ID:(1466, 0)

Concept

>Top

Dans le cas d'une somme où les éléments sont connectés en série, la résistance hydraulique totale du système est calculée en additionnant les résistances individuelles de chaque élément.

Étant donné que les éléments sont connectés en série, la chute de pression se produit dans chacun des éléments tandis que le débit reste constant. Par conséquent, a différence de pression totale ($\Delta p_t$) sera égal à la somme de a différence de pression dans un réseau ($\Delta p_k$). Chacun de ces éléments, conformément à la loi de Darcy, est égal à A resistência hidráulica em uma rede ($R_{hk}$) multiplié par le débit volumique dans un réseau ($J_{Vk}$) :

$\Delta p_k = R_{hk} J_{Vk}$

Ainsi, la somme de a resistência hidráulica em uma rede ($R_{hk}$) sera égale à A résistance hydraulique totale en série ($R_{st}$).

ID:(3630, 0)

Équation

>Top, >Modèle

Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) à partir de le rayon du cylindre ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :

nous pouvons identifier des paramètres liés à la géométrie (le longueur du tube ($\Delta L$) et le rayon du cylindre ($R$)) et au type de liquide (a viscosité ($\eta$)), qui peuvent être collectivement désignés sous le nom de une conductance hydraulique ($G_h$) :

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

Conditions

Variables

$G_h$

Conductance hydraulique

$m^4/kg s$

$\Delta L$

Longueur du tube

$m$

$\pi$

Pi

3.1415927

$rad$

$R$

Rayon du cylindre

$m$

$\eta$

Viscosité

$Pa s$

Relation

Développement

ID:(15102, 0)

Équation

>Top, >Modèle

Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons réécrire l'équation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) à l'aide de l'équation suivante :

$ J_V = G_h \Delta p $

Conditions

Variables

$G_h$

Conductance hydraulique

$m^4/kg s$

$\Delta p$

Différence de pression

$Pa$

$J_V$

Volumique flux

$m^3/s$

Relation

Développement

Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) à partir de le rayon du cylindre ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :

$ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

nous pouvons introduire a conductance hydraulique ($G_h$), défini en termes de le longueur du tube ($\Delta L$), le rayon du cylindre ($R$) et a viscosité ($\eta$), de la manière suivante :

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

pour obtenir :

$ J_V = G_h \Delta p $

ID:(14471, 0)

Équation

>Top, >Modèle

Dans le contexte de la résistance électrique, son inverse existe, connu sous le nom de conductance électrique. De manière similaire, ce qui serait a conductance hydraulique ($G_h$) peut être défini en termes de a résistance hydraulique ($R_h$) à travers l'expression :

$ R_h = \displaystyle\frac{1}{G_h }$

Conditions

Variables

$G_h$

Conductance hydraulique

$m^4/kg s$

$R_h$

Résistance hydraulique

$kg/m^4s$

Relation

.

ID:(15092, 0)

Équation

>Top, >Modèle

Puisque a résistance hydraulique ($R_h$) est égal à l'inverse de a conductance hydraulique ($G_h$), il peut être calculé à partir de l'expression de ce dernier. De cette manière, nous pouvons identifier des paramètres liés à la géométrie (le longueur du tube ($\Delta L$) et le rayon du cylindre ($R$)) et au type de liquide (a viscosité ($\eta$)), qui peuvent être collectivement désignés sous le nom de une résistance hydraulique ($R_h$) :

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

Conditions

Variables

$\Delta L$

Longueur du tube

$m$

$\pi$

Pi

3.1415927

$rad$

$R$

Rayon du cylindre

$m$

$R_h$

Résistance hydraulique

$kg/m^4s$

$\eta$

Viscosité

$Pa s$

Relation

Développement

Puisque a résistance hydraulique ($R_h$) est égal à A conductance hydraulique ($G_h$) conformément à l'équation suivante :

$ R_h = \displaystyle\frac{1}{G_h }$

et puisque a conductance hydraulique ($G_h$) est exprimé en termes de a viscosité ($\eta$), le rayon du cylindre ($R$), et le longueur du tube ($\Delta L$) comme suit :

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

nous pouvons en conclure que :

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

ID:(3629, 0)

Équation

>Top, >Modèle

Comme le volumique flux ($J_V$) peut être calculé à partir de a conductance hydraulique ($G_h$) et de a différence de pression ($\Delta p$) en utilisant l'équation suivante :

il peut être exprimé en termes de a différence de pression ($\Delta p$). En considérant que l'inverse de a résistance hydraulique ($R_h$) est a conductance hydraulique ($G_h$), nous obtenons l'expression suivante :

$ \Delta p = R_h J_V $

Conditions

Variables

$R_h$

Résistance hydraulique

$kg/m^4s$

$J_V$

Volumique flux

$m^3/s$

Relation

Développement

Dans le cas d'un seul cylindre a résistance hydraulique ($R_h$), qui dépend de a viscosité ($\eta$), le longueur du tube ($\Delta L$), et le rayon du cylindre ($R$), il est calculé à l'aide de l'équation suivante :

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

D'autre part, la loi de Hagen-Poiseuille permet de calculer le volumique flux ($J_V$) généré par a différence de pression ($\Delta p$) selon l'équation suivante :

$ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

En combinant ces deux équations, nous obtenons la loi de Darcy :

$ \Delta p = R_h J_V $

qu'Henry Darcy a formulée pour modéliser le comportement général de milieux poreux plus complexes à travers lesquels un liquide s'écoule.

Le génie de cette manière de réécrire la loi de Hagen-Poiseuille réside dans le fait qu'elle montre l'analogie entre l'écoulement du courant électrique et l'écoulement du liquide. Dans ce sens, la loi de Hagen-Poiseuille correspond à la loi d'Ohm. Cela ouvre la possibilité d'appliquer les concepts des réseaux électriques aux systèmes de canalisations à travers lesquels un liquide s'écoule.

Cette loi, également connue sous le nom de loi de Darcy-Weisbach, a été publiée pour la première fois dans l'uvre de Darcy :

• "Les fontaines publiques de la ville de Dijon", Henry Darcy, Victor Dalmont Editeur, Paris (1856).

ID:(3179, 0)

Équation

>Top, >Modèle

A différence de pression totale ($\Delta p_t$) par rapport aux différentes différence de pression dans un réseau ($\Delta p_k$), nous conduisant à la conclusion suivante :

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $

Conditions

Variables

Relation

ID:(4377, 0)

Équation

>Top, >Modèle

Dans le cas de ($$), sa valeur est calculée en utilisant a viscosité ($\eta$), le rayon du cylindre ($R$) et le longueur du tube ($\Delta L$) à travers l'équation suivante :

Lorsqu'il y a plusieurs résistances hydrauliques connectées en série, nous pouvons calculer a résistance hydraulique totale en série ($R_{st}$) en ajoutant a resistência hidráulica em uma rede ($R_{hk}$), comme exprimé dans la formule suivante :

$ R_{st} =\displaystyle\sum_k R_{hk} $

Conditions

Variables

$R_h$

Résistance hydraulique

$kg/m^4s$

$R_{ss}$

Resistência hidráulica em uma rede

$kg/m^4s$

Relation

Développement

Une manière de modéliser un tube avec une section transversale variable consiste à le diviser en sections de rayon constant et à additionner ensuite les résistances hydrauliques en série. Supposons que nous ayons une série de sections avec des rayons R_{hk} et des longueurs L_k. Les résistances hydrauliques correspondantes seraient

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

Dans chaque élément, il y aura une chute de pression égale là où le débit est le même, et la loi de Darcy s'applique :

$ \Delta p = R_h J_V $

La différence de pression totale sera égale à la somme des chutes de pression individuelles

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $

donc

$\Delta p=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$

Par conséquent, le système peut être modélisé comme un conduit unique avec une résistance hydraulique calculée comme la somme des composantes individuelles :

$ R_{st} =\displaystyle\sum_k R_{hk} $

ID:(3180, 0)

Concept

>Top

Dans le cas d'une somme où les éléments sont connectés en série, la conductance hydraulique totale du système est calculée en additionnant les conductances hydrauliques individuelles de chaque élément.

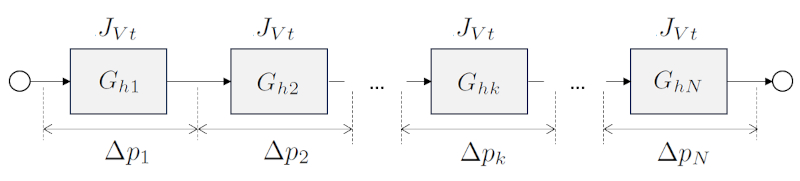
Étant donné que les éléments sont connectés en série, la chute de pression se produit dans chaque élément tandis que le débit reste constant. Par conséquent, a différence de pression totale ($\Delta p_t$) sera égal à la somme de a différence de pression dans un réseau ($\Delta p_k$). Chacun de ces éléments, conformément à la loi de Darcy, est égal à Le débit volumique dans un réseau ($J_{Vk}$) divisé par a conductance hydraulique dans un réseau ($G_{hk}$) :

$\Delta p_k = \displaystyle\frac{J_{Vk}}{K_{hk}}$

Ainsi, la somme de l'inverse de a conductance hydraulique dans un réseau ($G_{hk}$) sera égale à l'inverse de a conductance hydraulique de la série totale ($K_{st}$).

ID:(11067, 0)

Équation

>Top, >Modèle

Dans le cas de la somme d'éléments en série, a résistance hydraulique totale en série ($R_{st}$) est égal à la somme de a resistência hidráulica em uma rede ($R_{hk}$) :

Puisque a resistência hidráulica em uma rede ($R_{hk}$) est l'inverse de a conductance hydraulique dans un réseau ($G_{hk}$), nous avons :

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

Conditions

Variables

$R_{h1}$

Résistance hydraulique 1

$kg/m^4s$

$R_{h2}$

Résistance hydraulique 2

$kg/m^4s$

$R_{pt}$

Résistance hydraulique totale en parallèle

$kg/m^4s$

Relation

Développement

A résistance hydraulique totale en série ($R_{st}$), ainsi que a resistência hidráulica em uma rede ($R_{hk}$), dans

$ R_{st} =\displaystyle\sum_k R_{hk} $

et avec a conductance hydraulique dans un réseau ($G_{hk}$) et l'équation

$ R_h = \displaystyle\frac{1}{G_h }$

conduit à

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

ID:(3633, 0)

Description

>Top

Dans le cas de 3 résistances hydrauliques et en utilisant la loi de Darcy,

et la somme des pressions

ainsi que la somme en série des résistances hydrauliques

il est possible de calculer les chutes de pression en fonction des résistances hydrodynamiques et de la pression totale.

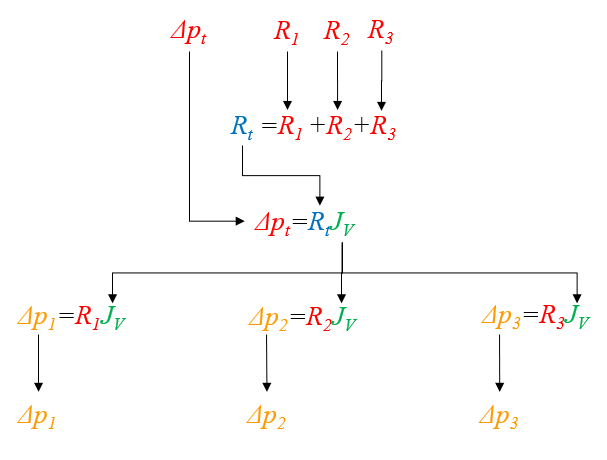
ID:(11069, 0)