Utilisateur:
Mesure de viscosité
Description
Si une petite sphère de rayon $a$ est laissée tomber dans un milieu de viscosité $\eta$, elle accélérera jusqu'à ce que la force gravitationnelle,
$mg=\displaystyle\frac{4\pi}{3}a^3\rho_sg$
où $\rho_s$ est la densité du matériau de la sphère, soit équilibrée par la force visqueuse,
$6\pi \eta a v$
où $v$ est la vitesse.
Il est donc possible d\'estimer la viscosité en mesurant la vitesse, car l\'équation suivante est vérifiée :
$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$
où le rayon peut être mesuré directement.
Ici, vous pouvez observer le comportement de la sphère :
ID:(9871, 0)
Expérience de vidage de colonne
Description
Cela signifie qu'à mesure que la colonne se vide et que la hauteur $h$ diminue, la vitesse $v$ diminue également de manière proportionnelle.
Les paramètres clés sont :
• Diamètre intérieur du récipient : 93 mm
• Diamètre intérieur du canal d\'évacuation : 3 mm
• Longueur du canal d\'évacuation : 18 mm
Ces paramètres sont importants pour comprendre et analyser le processus de vidage de la colonne et comment la vitesse de sortie varie avec la hauteur.
ID:(9870, 0)
Expérience de vidange de colonne: effet de viscosité
Description
Si nous analysons l\'équation
| $ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $ |
qui décrit l\'application de Hagen-Poiseuille, nous constatons que la courbe ne correspond qu\'aux données expérimentales dans les cas suivants :
La vitesse est faible (lorsque la colonne est presque vide).
Le rayon du canal d\'évacuation doit être réduit de 1,5 mm à 0,6 mm.
Cela montre que l\'écoulement est principalement turbulent et que seule à des niveaux de faible vitesse, la vitesse est suffisamment basse pour que le nombre de Reynolds soit faible et que l\'écoulement soit laminaire.
ID:(11065, 0)
Calcul de la viscosité
Image
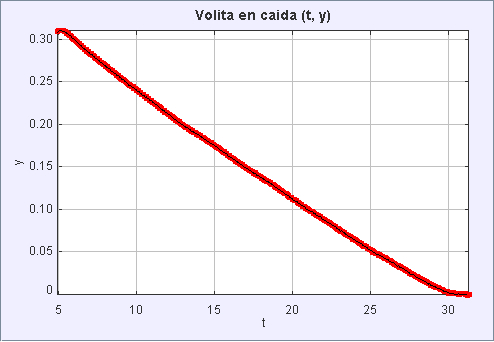
Si nous observons le trajet parcouru par la petite bille au fil du temps, nous pouvons constater qu'elle se déplace principalement à une vitesse constante d\'environ 0,31 mètres en 25 secondes, ce qui équivaut à 0,0124 m/s.
En réarrangeant l\'égalité entre la force gravitationnelle et la force de résistance de Stokes :
$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$
nous obtenons :
$\eta = \displaystyle\frac{2 a^2\rho_sg}{9 v}$
En supposant que la bille a un rayon de 2 mm et pèse 8 mg, nous pouvons déterminer sa densité à environ $\rho_s\sim 2,38 g/cm^3$. Par conséquent, la viscosité est estimée à environ $\eta\sim 1,67 Pa s$.
ID:(9881, 0)
Modèle
Concept
Variables
Paramètres
Paramètre sélectionné
Calculs
Équation
$h = h_0 e^{-t/\tau_{hp}}$
h = h_0 *exp(- t / tau_hp )
$ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $
S *DIFF(h,t,1) = - pi * R ^4 * rho * g * h /(8* eta * DL )
$ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$
S*DIFF(h,t,1) = pi * R ^2*sqrt(2* g * h )
$ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$
tau_hp = (8* eta * DL * S )/( pi * R ^4 * rho * g * h )
$ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $
v = rho * g * R ^2* h /(8* eta * l )
ID:(15494, 0)
Colonne de temps caractéristique avec liquide visqueux
Équation
Si nous examinons l'équation pour la vidange d'une colonne de liquide visqueux :
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
nous pouvons condenser les constantes en une unité de temps caractéristique :
 $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
Cette valeur devient un temps caractéristique pour la vidange d'une colonne de section transversale $S$ d'un liquide visqueux ayant une viscosité $\eta", à mesure qu'il s'écoule à travers un tube de rayon $R$.
ID:(14521, 0)
Hauteur de la colonne de liquide non visqueux au fil du temps
Équation
Pour le cas d'un liquide non visqueux s'écoulant de manière laminaire, la différence de pression générée par la colonne est la suivante :
| $ \Delta p = \rho_w g \Delta h $ |
Cela résulte en un écoulement de vitesse $v$ à travers un tube selon le principe de Bernoulli:
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Étant donnée la vitesse et le rayon du tube, nous pouvons calculer le débit, qui est lié au débit à l'intérieur de la colonne par la loi de continuité. À son tour, cela est lié à la variation de la hauteur $h", comme décrit dans:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
En utilisant l'équation de Bernoulli, nous pouvons analyser le cas d'une colonne d'eau qui génère une différence de pression :
| $ \Delta p = \rho_w g \Delta h $ |
et induit un écoulement de vitesse $v$ à travers un tube, conformément à :
| $ \Delta p = - \rho \bar{v} \Delta v $ |
Ainsi, nous pouvons estimer la vitesse comme suit :
$v = \sqrt{2 g h}$
Cette vitesse, à travers une section de tube de rayon $R$, entraîne un débit :
$J = \pi R^2 v$
Si la colonne a une aire de section transversale $S$ et que sa hauteur diminue par rapport à la variation de la hauteur $h$ au fil du temps $t$, nous pouvons appliquer la loi de la continuité, qui énonce :
| $ S_1 j_{s1} = S_2 j_{s2} $ |
Par conséquent, l'équation qui décrit cette situation est :
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
ID:(9882, 0)
Expérience de vidange de colonne : modèle avec Bernoulli
Description
Considérons le système d'un seau cylindrique avec un trou de drainage. Lorsque le bouchon est retiré, l\'eau commence à s\'écouler en fonction de la pression existante. Selon le principe de Bernoulli, à l'intérieur du seau ($v\sim 0$), la vitesse est nulle, et nous avons :
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$
tandis qu\'à l\'extérieur du seau ($h=0$), seule la composante cinétique existe :
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$
Comme les deux expressions sont égales, nous avons :
$\displaystyle\frac{1}{2}\rho v^2=\rho g h$
ce qui donne la vitesse comme :
$v=\sqrt{2 g h}$
Pour comparer avec l\'expérience, nous pouvons utiliser cette expression pour estimer, avec :
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
la portée que le jet d\'eau devrait avoir. Si nous le représentons graphiquement, nous observons :
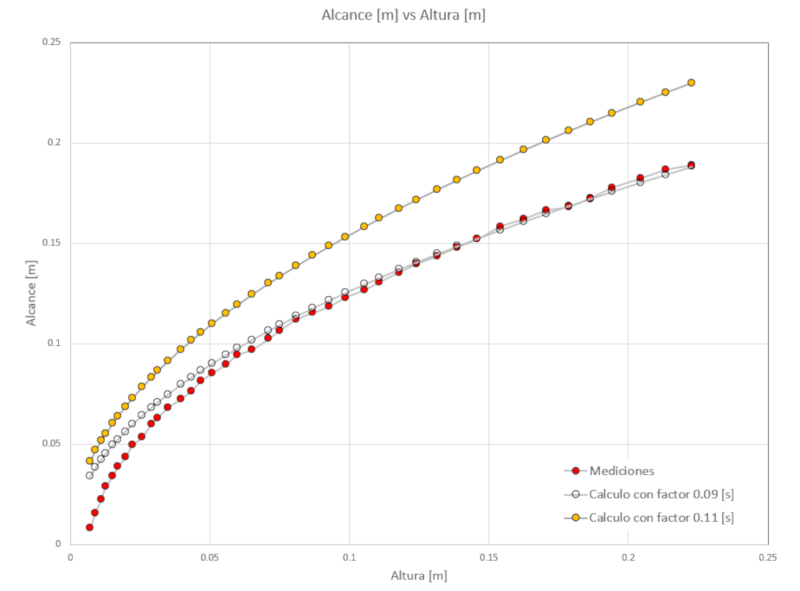
où :
• les points rouges correspondent aux mesures expérimentales,
• les points bleus correspondent à la portée calculée en utilisant un facteur de 0,11,
• les points transparents correspondent à la portée calculée en utilisant un facteur de 0,09.
Par conséquent, nous pouvons conclure que le modèle de Bernoulli surestime la vitesse à laquelle le seau se vide. Cela est dû au fait que dans la région du trou de drainage, les effets de la viscosité ne sont pas négligeables, et donc la vitesse est plus faible.
ID:(11063, 0)
Expérience de coulée de colonne: modèle avec Hagen Poiseuille
Équation
Étant donné le modèle de l\'écoulement d\'un liquide visqueux à travers un tube et en considérant que la hauteur de la colonne détermine la pression, nous pouvons estimer la vitesse en fonction de la hauteur de la colonne:
| $ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $ |
Si nous considérons que le canal de drainage présente une résistance hydraulique, nous pouvons le modéliser avec l\'équation de Hagen-Poiseuille :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
où la différence de pression est déterminée par la colonne d\'eau :
| $ p = \rho_w g h $ |
et la vitesse est obtenue à travers le débit :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
De cette manière, nous obtenons la relation pour calculer la vitesse en fonction de la hauteur :
| $ v = \displaystyle\frac{ \rho g R ^2}{8 \eta \Delta L } h $ |
ID:(11064, 0)
Hauteur de la colonne de liquide visqueux au fil du temps
Équation
L'écoulement laminaire d'un fluide de viscosité $\eta$ à travers un tube de rayon $R$ est décrit par la loi de Hagen-Poiseuille :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
La différence de pression est déterminée par la hauteur de la colonne $\Delta h$ :
| $ \Delta p = \rho_w g \Delta h $ |
qui diminue à mesure que le liquide s'écoule. En appliquant l'équation de continuité, nous pouvons démontrer que la hauteur diminue au fil du temps comme suit :
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
Si le débit à travers le tube est décrit par l'équation :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
et que la différence de pression $\Delta p$ est proportionnelle à la hauteur de la colonne $\Delta h = h :
| $ \Delta p = \rho_w g \Delta h $ |
nous pouvons appliquer la conservation du débit $J_{V1}=J_V$ entre le tube et la colonne $J_{V2}$ :
| $ J_{V1} = J_{V2} $ |
,
où le débit dans la colonne $J_{V2}$ avec une section transversale $S$ est donné par :
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Ici, la densité de flux $j_s$ correspond à la vitesse moyenne, qui est égale au taux de changement de la hauteur au fil du temps :
$j_s = \displaystyle\frac{dh}{dt}$
De cette manière, nous obtenons l'équation pour la hauteur de la colonne en fonction du temps :
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
ID:(14520, 0)
Evolution temporelle de la colonne de liquide visqueux
Équation
L'équation qui décrit l'évolution de la colonne de liquide visqueux en train de se vider est la suivante :
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
Nous pouvons réécrire cette équation en utilisant le temps caractéristique :
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
Suite à l'intégration, nous obtenons :
| $h = h_0 e^{-t/\tau_{hp}}$ |
Si dans l'équation
| $ S \displaystyle\frac{dh}{dt} = - \displaystyle\frac{\pi R^4}{\Delta L}\displaystyle\frac{\rho g}{8 \eta} h $ |
les constantes sont remplacées par
| $ \tau_{hp} = \displaystyle\frac{S \Delta L}{\pi R^4}\displaystyle\frac{8 \eta}{\rho g}$ |
nous obtenons l'équation différentielle linéaire du premier ordre
$\displaystyle\frac{dh}{dt}=\displaystyle\frac{1}{\tau_{hp}} h$
dont la solution est
| $h = h_0 e^{-t/\tau_{hp}}$ |
où $h_0$ représente la hauteur initiale.
ID:(14522, 0)