Kolumnencasting mit Hagen Poiseuille
Storyboard 
Es handelt sich um einen Wassersäule mit einem Loch im unteren Teil. Das Entleeren wird überwacht, wobei eine Ausgabegeschwindigkeit abhängig von der Höhe der Säule erhalten wird.Wenn die Daten mit Bernoulli modelliert werden, der Ausgang durch das Loch jedoch mit Hagen Poiseville modelliert wird, wird das Problem des Falls behoben, in dem angenommen wurde, dass es keine Viskosität gibt.
ID:(1428, 0)
Viskositätsmessung
Beschreibung 
Wenn eine kleine Kugel mit dem Radius $a$ in ein Medium mit Viskosität $\eta$ fallen gelassen wird, beschleunigt sie, bis die Gravitationskraft
$mg=\displaystyle\frac{4\pi}{3}a^3\rho_sg$
wobei $\rho_s$ die Dichte des Kugelmaterials ist, gleich der Viskositätskraft ist
$6\pi \eta a v$
wobei $v$ die Geschwindigkeit ist.
Daher ist es möglich, die Viskosität durch Messung der Geschwindigkeit abzuschätzen, da gilt:
$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$
wobei der Radius direkt gemessen werden kann.
Hier können Sie das Verhalten der Kugel beobachten:
ID:(9871, 0)
Experiment zum entleeren von Säulen
Beschreibung 
Dies bedeutet, dass sich mit dem Abnehmen der Säule und der Verringerung der Höhe $h$ auch die Geschwindigkeit $v$ proportional verringert.
Die Schlüsselparameter sind:• Innen-Durchmesser des Gefäßes: 93 mm• Innen-Durchmesser des Evakuierungskanals: 3 mm• Länge des Evakuierungskanals: 18 mmDiese Parameter sind wichtig, um den Prozess des Säulenentleerens zu verstehen und zu analysieren, sowie wie sich die Austrittsgeschwindigkeit mit der Höhe ändert.
ID:(9870, 0)
Säulenentleerungsexperiment: Viskositätseffekt
Beschreibung 
Wenn wir die Gleichung
| $ j_s = \displaystyle\frac{ \rho_w g R ^2}{8 \eta \Delta L } h $ |
analysieren, die die Anwendung von Hagen-Poiseuille beschreibt, stellen wir fest, dass die Kurve nur mit den experimentellen Daten in folgenden Fällen übereinstimmt:
Die Geschwindigkeit ist niedrig (wenn die Säule fast leer ist).
Der Radius des Evakuierungskanals muss von 1,5 mm auf 0,6 mm reduziert werden.

Dies zeigt, dass der Fluss hauptsächlich turbulent ist und dass nur bei niedrigen Geschwindigkeiten die Geschwindigkeit niedrig genug ist, damit die Reynolds-Zahl niedrig ist und der Fluss laminar ist.
ID:(11065, 0)
Viskositätsberechnung
Bild 
Wenn wir den Weg betrachten, den das kleine Kugelchen im Laufe der Zeit zurücklegt, können wir feststellen, dass es größtenteils mit einer konstanten Geschwindigkeit von etwa 0,31 Metern in 25 Sekunden oder 0,0124 m/s vorankommt.
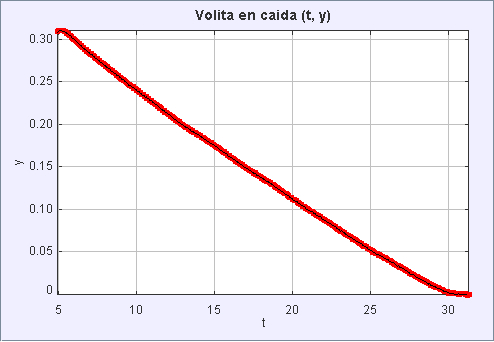
Durch Umstellen der Gleichung zwischen der Gravitationskraft und der Stokeschen Widerstandskraft:
$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$
erhalten wir:
$\eta = \displaystyle\frac{2 a^2\rho_sg}{9 v}$
Angenommen, die Kugel hat einen Radius von 2 mm und wiegt 8 mg, können wir ihre Dichte auf etwa $\rho_s\sim 2,38,g/cm^3$ bestimmen. Daher wird die Viskosität auf ungefähr $\eta\sim 1,67 Pa s$ geschätzt.
ID:(9881, 0)
Experiment zum Entleeren von Säulen: Model mit Bernoulli
Beschreibung 
Betrachten wir das System eines zylindrischen Eimers mit einem Abflussloch. Wenn der Stopfen entfernt wird, beginnt das Wasser aufgrund des vorhandenen Drucks zu fließen. Gemäß dem Bernoulli-Prinzip ist die Geschwindigkeit im Inneren des Eimers ($v\sim 0$) null, und wir haben:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$
während außerhalb des Eimers ($h=0$) nur die kinetische Komponente vorhanden ist:
$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$
Da beide Ausdrücke gleich sind, haben wir:
$\displaystyle\frac{1}{2}\rho v^2=\rho g h$
was zur Geschwindigkeit führt:
$v=\sqrt{2 g h}$
Um den Versuch mit der Theorie zu vergleichen, können wir diesen Ausdruck verwenden, um mit:
| $ S\displaystyle\frac{dh}{dt} = \pi R^2 \sqrt{2gh}$ |
die Reichweite zu berechnen, die der Strahl haben sollte. Wenn wir dies grafisch darstellen, beobachten wir:
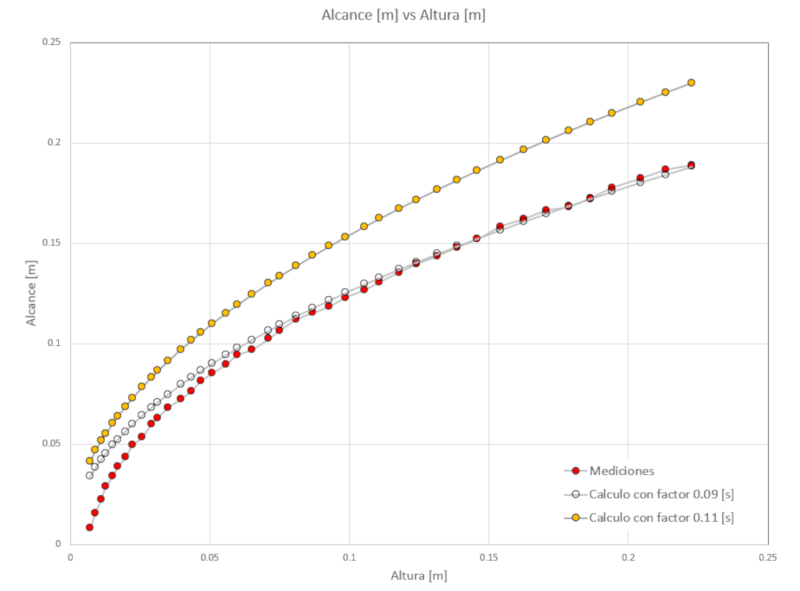
wo:• die roten Punkte den experimentellen Messungen entsprechen,• die blauen Punkte der berechneten Reichweite unter Verwendung eines Faktors von 0,11 entsprechen,• die transparenten Punkte der berechneten Reichweite unter Verwendung eines Faktors von 0,09 entsprechen.Daher können wir folgern, dass das Bernoulli-Modell die Geschwindigkeit, mit der der Eimer sich entleert, überschätzt. Dies liegt daran, dass in der Nähe des Abflusslochs die Auswirkungen der Viskosität nicht vernachlässigbar sind und die Geschwindigkeit daher geringer ist.
ID:(11063, 0)
