Câble
Storyboard 
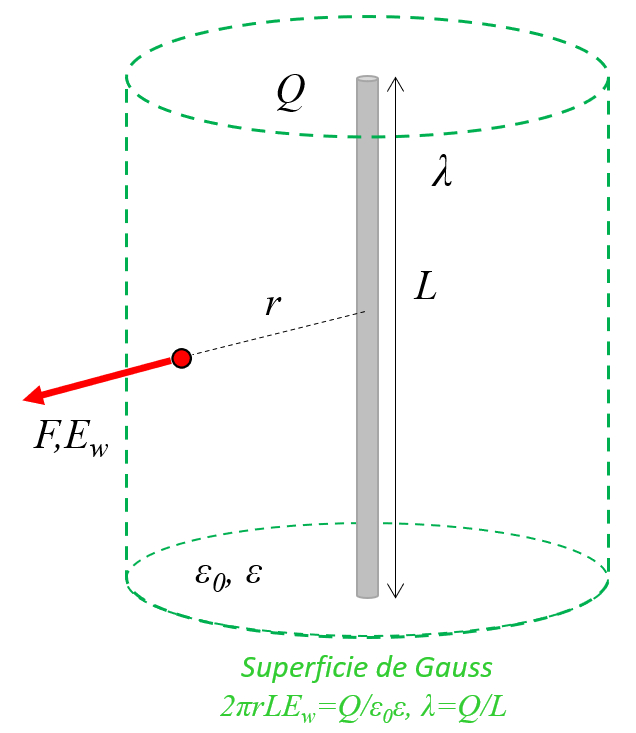
La géométrie désignée comme un fil peut être comprise comme un cylindre de hauteur infinie, où la distance à l'axe est bien plus grande que le rayon du cylindre. Essentiellement, cela correspond à un cas où le rayon tend vers zéro, devenant effectivement une ligne de charge infiniment fine.
ID:(2073, 0)
Câble
Storyboard 
La géométrie désignée comme un fil peut être comprise comme un cylindre de hauteur infinie, où la distance à l'axe est bien plus grande que le rayon du cylindre. Essentiellement, cela correspond à un cas où le rayon tend vers zéro, devenant effectivement une ligne de charge infiniment fine.
Variables
Calculs
Calculs
Équations
Dans le cas d'une surface gaussienne sph rique, le champ électrique ($\vec{E}$) est constant dans la direction de le versor normal à la section ($\hat{n}$). Par cons quent, en utilisant a charge ($Q$), a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$), il peut tre calcul en int grant sur a surface sur laquelle le champ électrique est constant ($dS$) :
Avec a surface ($S$) pour un cylindre de a distance à l'axe ($r$) et le longueur du pilote ($L$) :
et a densité de charge linéaire ($\lambda$) calcul avec a charge ($Q$) :
Ainsi,
Dans le cas d'une surface gaussienne sph rique, le champ électrique ($\vec{E}$) est constant dans la direction de le versor normal à la section ($\hat{n}$). Par cons quent, en utilisant a charge ($Q$), a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$), il peut tre calcul en int grant sur a surface sur laquelle le champ électrique est constant ($dS$) :
Avec a surface ($S$) pour un cylindre de a distance à l'axe ($r$) et le longueur du pilote ($L$) :
et a densité de charge linéaire ($\lambda$) calcul avec a charge ($Q$) :
Ainsi,
Le potentiel électrique, fil infini ($\varphi_w$) est d riv de l'int gration radiale de le champ électrique d'un fil infini ($E_w$) de le rayon de référence ($r_0$) A distance à l'axe ($r$), r sultant dans l' quation suivante :
De plus, pour les variables a charge ($Q$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), la valeur de le champ électrique d'un fil infini ($E_w$) est donn e par :
Cela implique que par l'ex cution de l'int gration
$\varphi_w = -\displaystyle\int_{r_0}^r du \displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon u }= -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon } \ln\left(\displaystyle\frac{ r }{ r_0 }\right)$
l' quation suivante est obtenue :
Le potentiel électrique, fil infini ($\varphi_w$) est d riv de l'int gration radiale de le champ électrique d'un fil infini ($E_w$) de le rayon de référence ($r_0$) A distance à l'axe ($r$), r sultant dans l' quation suivante :
De plus, pour les variables a charge ($Q$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), la valeur de le champ électrique d'un fil infini ($E_w$) est donn e par :
Cela implique que par l'ex cution de l'int gration
$\varphi_w = -\displaystyle\int_{r_0}^r du \displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon u }= -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon } \ln\left(\displaystyle\frac{ r }{ r_0 }\right)$
l' quation suivante est obtenue :
Exemples
Dans le cas d'une surface gaussienne sph rique, le champ électrique ($\vec{E}$) est constant dans la direction de le versor normal à la section ($\hat{n}$). Par cons quent, en utilisant a charge ($Q$), a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$), il peut tre calcul en int grant sur a surface sur laquelle le champ électrique est constant ($dS$) :
Avec a surface ($S$) pour un cylindre de a distance à l'axe ($r$) et le longueur du pilote ($L$) :
ce qui est montr dans le graphique
et a densité de charge linéaire ($\lambda$) calcul avec a charge ($Q$) :
Ainsi,
Le potentiel électrique, fil infini ($\varphi_w$) est d riv de l'int gration radiale de le champ électrique d'un fil infini ($E_w$) de le rayon de référence ($r_0$) A distance à l'axe ($r$), r sultant dans l' quation suivante :
De plus, pour les variables a charge ($Q$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), la valeur de le champ électrique d'un fil infini ($E_w$) est donn e par :
Cela implique que par l'ex cution de l'int gration
$\varphi_w = -\displaystyle\int_{r_0}^r du \displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon u }= -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon } \ln\left(\displaystyle\frac{ r }{ r_0 }\right)$
l' quation suivante est obtenue :
Comme illustr dans le graphique suivant :
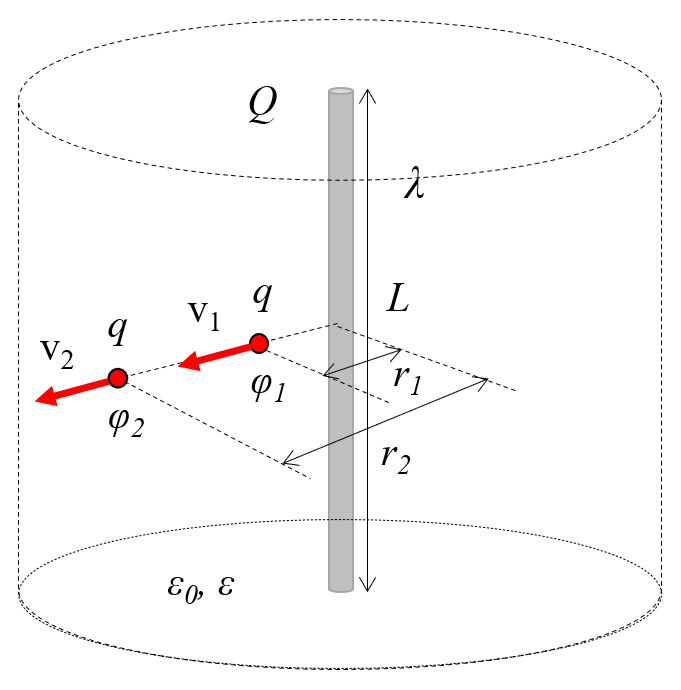
le champ en deux points doit poss der la m me nergie. Par cons quent, les variables a charge ($Q$), a masse molaire ($m$), a vitesse 1 ($v_1$), a vitesse 2 ($v_2$) et le potentiel électrique 1 ($\varphi_1$) selon l' quation :
et le potentiel électrique 2 ($\varphi_2$), selon l' quation :
doivent satisfaire la relation suivante :
Le champ électrique d'un fil infini ($E_w$) est une fonction de a densité de charge linéaire ($\lambda$), a distance à l'axe ($r$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$) et est calcul travers:
A densité de charge linéaire ($\lambda$) est calcul comme a charge ($Q$) divis par le longueur du pilote ($L$)xa0:
Le champ électrique d'un fil infini ($E_w$) est une fonction de a densité de charge linéaire ($\lambda$), a distance à l'axe ($r$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$) et est calcul travers:
Le potentiel électrique, fil infini ($\varphi_w$) c'est avec le pi ($\pi$), a constante de champ électrique ($\epsilon_0$), a constante diélectrique ($\epsilon$), a densité de charge linéaire ($\lambda$), a distance à l'axe ($r$) et le rayon de référence ($r_0$) est gal :
Le potentiel électrique, fil infini ($\varphi_w$) c'est avec le pi ($\pi$), a constante de champ électrique ($\epsilon_0$), a constante diélectrique ($\epsilon$), a densité de charge linéaire ($\lambda$), a distance à l'axe ($r$) et le rayon de référence ($r_0$) est gal :
Les potentiels lectriques, qui repr sentent l' nergie potentielle par unit de charge, influencent la variation de la vitesse d'une particule. Par cons quent, en raison de la conservation de l' nergie entre deux points, il s'ensuit que en pr sence des variables a charge ($q$), a masse molaire ($m$), a vitesse 1 ($v_1$), a vitesse 2 ($v_2$), le potentiel électrique 1 ($\varphi_1$), et le potentiel électrique 2 ($\varphi_2$), la relation suivante doit tre respect e :
ID:(2073, 0)