Capacitors
Storyboard 
Capacitors are elements that allow circuits to dynamically store charge. They are pollinated and can discharge depending on how they are applied potentials that charge or discharge charges on their plates.
ID:(1579, 0)
Capacitors example
Definition 
Los capacitores son elementos que se reconocen por tener
• dos contactos (cuidado la mayoría tiene dos)
• ser un cilindro o un bulto
Por problemas de disipar calor y no interferir por las cargas que almacena por lo general no esta integrado en el circuito y sobresale:

ID:(11703, 0)
Capacity Units
Image 
La capacidad se define como la relación entre la carga y el potencial eléctrico:
| $ \Delta\varphi =\displaystyle\frac{ Q }{ C }$ |
El primero se mide en Coulomb, el segundo en Volt. La división de Coulomb [C] por Volt [V] se denomina el Farad en honor a Michael Faraday.
Sin embargo la capacidad que se usa habitualmente es mucho mas chica que el Farad [F] por lo que los condensadores se indican en micro, nano y picofaradios:
| Microfarad $\mu F$ | $10^{-6} F$ |
| Nanofarad $nF$ | $10^{-9} F$ |
| Picofarad $pF$ | $10^{-12} F$ |
El Farad es MKS, micro, nano y pico Farad no.
ID:(11714, 0)
Circuit diagram
Note 
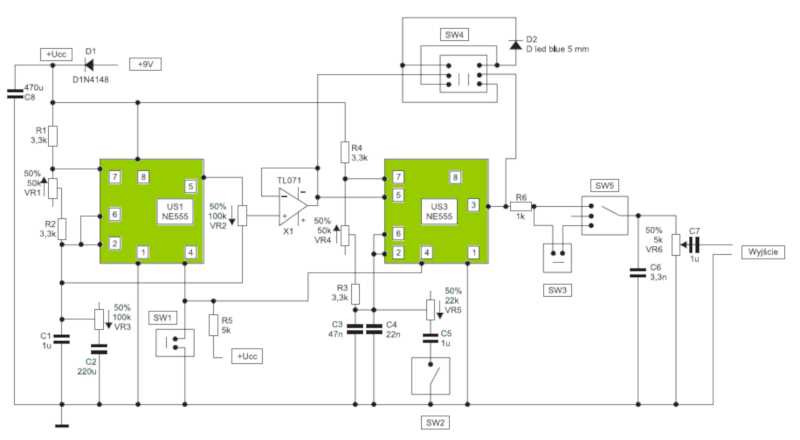
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con números)
ID:(11704, 0)
Example of printed circuit
Quote 
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con métodos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• procesadores (cajas rectangulares con números)

ID:(11705, 0)
Parallel plates, geometry
Exercise 
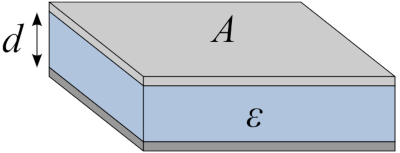
Dos placas paralelas con un dieléctrico entre ellos forman un condensador:
ID:(11706, 0)
Concentric cylinders, geometry
Equation 
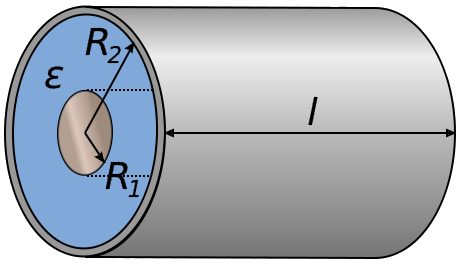
Dos cilindros concentricos con un dieléctrico entre ellos forman un condensador:
ID:(11707, 0)
Concentric spheres, geometry
Script 
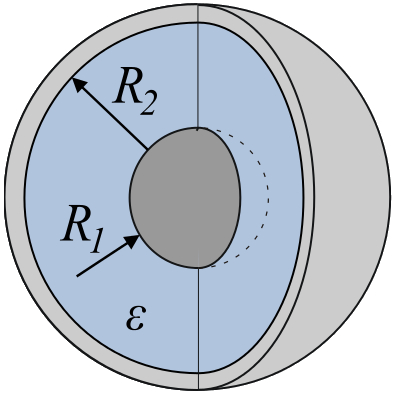
Dos esferas concentricas con un dieléctrico entre ellas forman un condensador:
ID:(11709, 0)
Parallel wires, geometry
Variable 
Dos alambres pueden formar entre ellos un condensador:
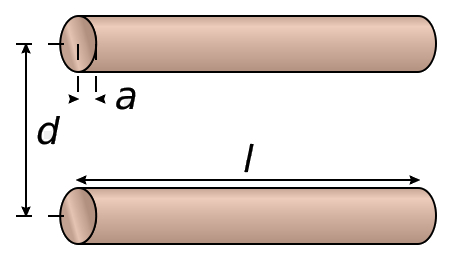
Esto puede ser también involuntario.
ID:(11708, 0)
Capacitors
Description 
Capacitors are elements that allow circuits to dynamically store charge. They are pollinated and can discharge depending on how they are applied potentials that charge or discharge charges on their plates.
Variables
Calculations
Calculations
Equations
None
(ID 3218)
Examples
Al conectar capacidades en paralelo ca da de potencial
$Q=\displaystyle\sum_i Q_i$
Si ahora se aplica la relaci n de las capacidades para cada una de estas se tendr para potenciales iguales que
$\Delta\varphi=\displaystyle\frac{Q_i}{C_i}$
Con ello la carga total es igual a
$Q=\displaystyle\sum_i C_i\Delta\varphi$
por lo que la regla de suma de capacidades en paralelo ser con
| $ C_p =\displaystyle\sum_ i C_i $ |
(ID 3218)
Los capacitores son elementos que se reconocen por tener
• dos contactos (cuidado la mayor a tiene dos)
• ser un cilindro o un bulto
Por problemas de disipar calor y no interferir por las cargas que almacena por lo general no esta integrado en el circuito y sobresale:

(ID 11703)
La capacidad se define como la relaci n entre la carga y el potencial el ctrico:
| $ \Delta\varphi =\displaystyle\frac{ Q }{ C }$ |
El primero se mide en Coulomb, el segundo en Volt. La divisi n de Coulomb [C] por Volt [V] se denomina el Farad en honor a Michael Faraday.
Sin embargo la capacidad que se usa habitualmente es mucho mas chica que el Farad [F] por lo que los condensadores se indican en micro, nano y picofaradios:
| Microfarad $\mu F$ | $10^{-6} F$ |
| Nanofarad $nF$ | $10^{-9} F$ |
| Picofarad $pF$ | $10^{-12} F$ |
El Farad es MKS, micro, nano y pico Farad no.
(ID 11714)
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con n meros)

(ID 11704)
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con m todos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• procesadores (cajas rectangulares con n meros)

(ID 11705)
Dos placas paralelas con un diel ctrico entre ellos forman un condensador:

(ID 11706)
La capacidad de un capacitor formado por dos placas paralelas es con igual a
| $ C_p = \displaystyle\frac{ \epsilon \epsilon_0 S }{ d }$ |
(ID 11713)
Dos cilindros concentricos con un diel ctrico entre ellos forman un condensador:

(ID 11707)
La capacidad de un capacitor formado por dos cilindros concentricos es con
| $ C_c = \displaystyle\frac{2 \pi \epsilon \epsilon_0 L }{\ln\left(\displaystyle\frac{ R_2 }{ R_1 }\right)}$ |
(ID 11711)
Dos esferas concentricas con un diel ctrico entre ellas forman un condensador:

(ID 11709)
La capacidad de un capacitor formado por dos esferas concentricas es con
| $ C_s = \displaystyle\frac{4 \pi \epsilon \epsilon_0 }{\displaystyle\frac{ 1 }{ R_1 }-\displaystyle\frac{ 1 }{ R_2 }}$ |
(ID 11712)
Dos alambres pueden formar entre ellos un condensador:

Esto puede ser tambi n involuntario.
(ID 11708)
La capacidad de un capacitor formado por dos alambres es con igual a
| $ C_w = \displaystyle\frac{ \pi \epsilon \epsilon_0 L }{arccosh\left(\displaystyle\frac{ d }{2 a }\right)}$ |
(ID 11710)
ID:(1579, 0)
