Storyboard

Les oiseaux ont une manière très particulière de voler qui les distingue des techniques utilisées par les humains dans leurs aéronefs. Dans ce cas, les ailes ont une double fonction, générant à la fois de la portance et de la poussée, même lorsque l'oiseau est immobile.

>Modèle

ID:(2056, 0)

Iframe

>Top

ID:(15178, 0)

Concept

>Top

Si vous étudiez la vidéo d'un pigeon volant d'une perspective latérale, vous pouvez observer comment il avance et rétracte ses ailes.

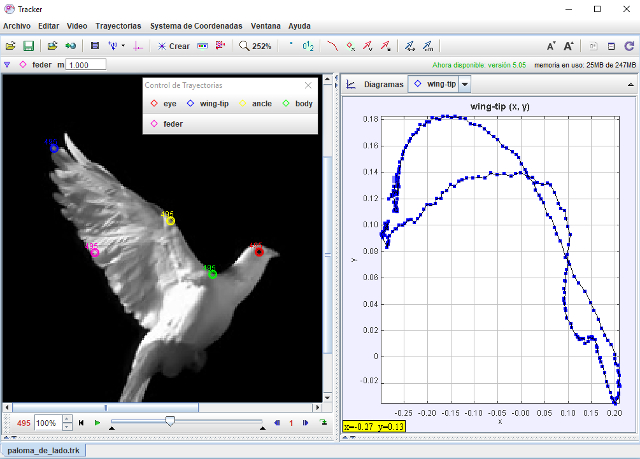
Pendant la phase d'avancement, l'oiseau parvient à générer de la portance, tandis qu'en reculant, il cherche à se propulser.

ID:(1587, 0)

Concept

>Top

Si vous étudiez la vidéo d'un pigeon volant en perspective frontale, vous pouvez observer comment il déploie et rétracte ses ailes.

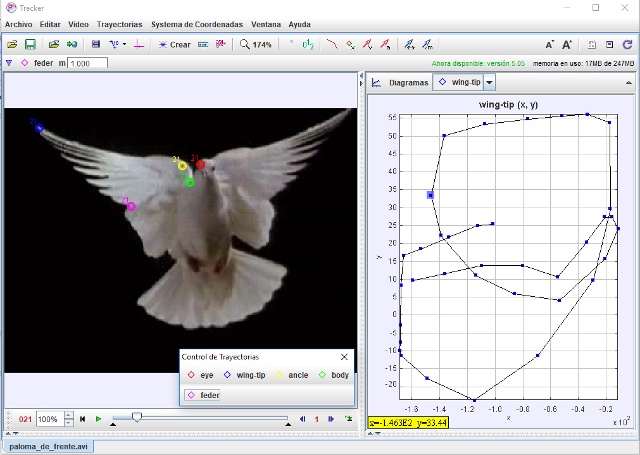
Pendant la phase d'avancement, l'oiseau déploie ses ailes pour la première fois afin de générer de la portance, tandis que pendant la phase de recul, il les déploie une deuxième fois pour se propulser vers l'avant.

ID:(1589, 0)

Description

>Top

Pour modéliser l'aile, il est nécessaire d'estimer a envergure des ailes ($L$), la largeur le largeur de l'aile ($w$) et a hauteur de l'aile ($d$) de l'aile afin de calculer a surface génératrice de portance ($S_w$) et le profil total de l'objet ($S_p$). Un article avec des données sur les oiseaux migrateurs peut être trouvé dans [1] :

Remarque : Dans ce cas, les surfaces alaires et les envergures sont fournies, ce qui permet d'estimer la largeur comme $S_w/L$. De même, la hauteur de l'aile peut être estimée à partir de la surface de la section du profil divisée par l'envergure $S_p/L$, bien que dans ce cas, nous ne prenions pas en compte que le profil inclut la section du corps de l'oiseau.

[1] "Field Estimates of Body Drag Coefficient on the basis of dives in passerine Birds" (Estimations de terrain du coefficient de traînée corporelle basées sur les plongées chez les oiseaux Passeriformes), Anders Hedenström, Felix Liechti, The Journal of Experimental Biology, 204, 1167-1175 (2001).

ID:(1585, 0)

Image

>Top

Lorsque nous comparons différents types d'ailes, nous remarquons que les oiseaux de proie ont tendance à avoir des ailes plus courtes et plus larges, tandis que les oiseaux migrateurs ont des ailes plus longues et plus étroites. Par conséquent, il est logique de définir le relación de aspecto ($\gamma_w$) comme la relation entre a envergure des ailes ($L$) et le largeur de l'aile ($w$) :

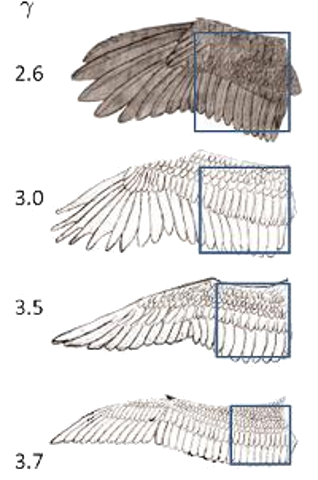
ID:(7043, 0)

Top

>Top

ID:(15191, 0)

Équation

>Top, >Modèle

A surface génératrice de portance ($S_w$) peut être estimé en utilisant a envergure des ailes ($L$) et le largeur de l'aile ($w$) comme suit :

$ S_w = L \Delta $

Conditions

Variables

$L$

Envergure des ailes

$m$

6337

$\Delta$

Largeur de l'aile

$m$

6336

$S_w$

Surface génératrice de portance

$m^2$

6117

Relation

ID:(4553, 0)

Équation

>Top, >Modèle

Le profil total de l'objet ($S_p$) peut être estimé en utilisant a envergure des ailes ($L$) et a hauteur de l'aile ($d$) comme suit :

$ S_p = L \delta $

Conditions

Variables

$L$

Envergure des ailes

$m$

6337

$\delta$

Hauteur de l'aile

$m$

6338

$S_p$

Profil total de l'objet

$m^2$

6123

Relation

ID:(4554, 0)

Équation

>Top, >Modèle

Le relación de aspecto ($\gamma_w$) est défini comme le rapport entre le largeur de l'aile ($w$) et a envergure des ailes ($L$), indiquant la proportion ou la relation entre ces deux variables :

$ \gamma_w =\displaystyle\frac{ w }{ L }$

Conditions

Variables

$L$

Envergure des ailes

$m$

6337

$w$

Largeur de l'aile

$m$

6336

$\gamma_w$

Relación de aspecto

$-$

6334

Relation

ID:(4551, 0)

Équation

>Top, >Modèle

Le relación de aspecto ($\gamma_w$) peut être défini comme le rapport épaisseur/portée ($\gamma_d$), qui relie le largeur de l'aile ($w$) à ($$)6338

$ \gamma_r =\displaystyle\frac{ d }{ w }$

Conditions

Variables

$d$

Hauteur de l'aile

$m$

6338

$w$

Largeur de l'aile

$m$

6336

$\gamma_r$

Rapport épaisseur/portée

$-$

6344

Relation

ID:(4555, 0)

Équation

>Top, >Modèle

Tout comme a profil total de l'objet ($P$) est lié à A densité ($\rho$), le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$), a constante de proportionnalité du coefficient de portance ($c$), a surface génératrice de portance ($S_w$) et a vitesse par rapport au milieu ($v$) à travers

,

nous pouvons exprimer la puissance en termes de le relación de aspecto ($\gamma_w$) et le rapport épaisseur/portée ($\gamma_d$) comme

$ P_w =\displaystyle\frac{1}{2} \rho L ^2 C_w v ^3\displaystyle\frac{1}{ \gamma_p }+\displaystyle\frac{2 m ^2 g ^2}{ c ^2 L ^2 \rho } \gamma_w \displaystyle\frac{1}{ v }$

Conditions

Variables

Relation

Développement

Comme a profil total de l'objet ($P$) est lié à A densité ($\rho$), le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a masse corporelle ($m$), a accélération gravitationnelle ($g$), a constante de proportionnalité du coefficient de portance ($c$), a surface génératrice de portance ($S_w$), et a vitesse par rapport au milieu ($v$) à travers

,

en plus des définitions de a surface génératrice de portance ($S_w$) en termes de le largeur de l'aile ($w$)

,

et de le relación de aspecto ($\gamma_w$)

,

ainsi que de a masse corporelle de l'avion ($m_p$) par rapport à A hauteur de l'aile ($d$)

,

et de le rapport épaisseur/portée ($\gamma_d$)

,

enfin, comme

.

.

ID:(9593, 0)