Velocidad constante
Storyboard 
Para describir cómo evoluciona la posición en el tiempo, es necesario analizar la variación de ésta a lo largo del tiempo.
La relación entre la variación de la posición equivale a la distancia recorrida en el tiempo transcurrido, que, al dividirla por dicho tiempo, se convierte en la velocidad.
Cuando se considera un intervalo de tiempo finito, la velocidad representa la velocidad promedio durante ese lapso.
ID:(608, 0)
Mecanismos
Definición 
La clave del modelo para describir un movimiento a velocidad constante es comprender el concepto de
• posición,
• camino recorrido,
• tiempo y
• tiempo transcurrido
para definir la velocidad. Por ultimo se discute la representación grafica y su interpretación.
ID:(15379, 0)
Posición
Imagen 
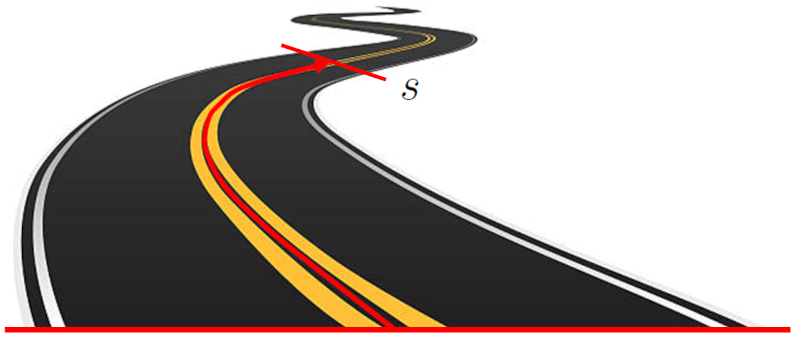
La posición ($s$) de un objeto en un sistema unidimensional se refiere a la ubicación del objeto en relación con un punto de referencia. Esta ubicación se expresa como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta en un eje cartesiano, o puede seguir un camino curvo:
ID:(15, 0)
Posición inicial
Nota 
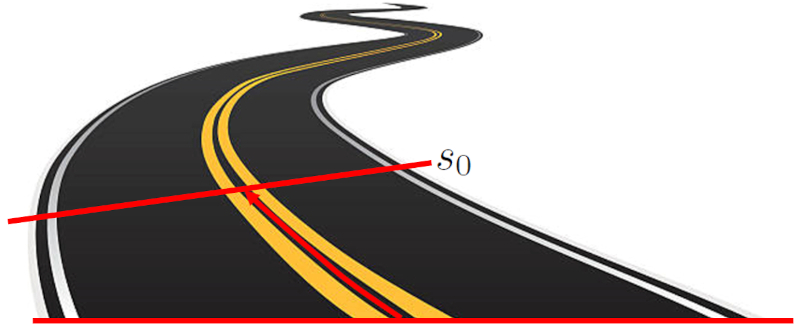
La posición inicial ($s_0$) es la ubicación inicial de un objeto antes de que comience un movimiento. Esta ubicación se define como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta sobre un eje cartesiano, o puede seguir una trayectoria curva.
ID:(10302, 0)
Distancia recorrida
Cita 
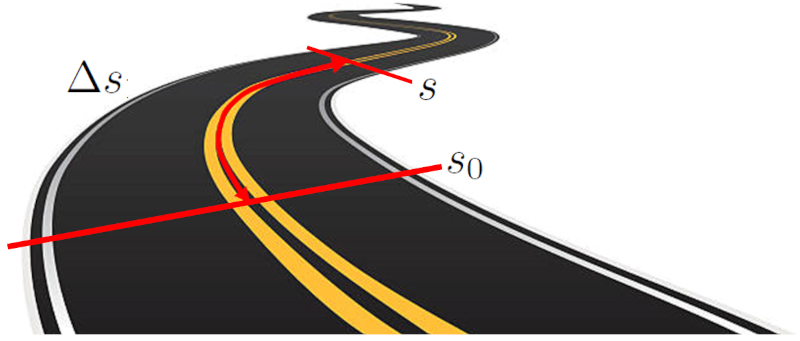
La distancia recorrida en un tiempo ($\Delta s$) por un objeto se mide midiendo la distancia entre dos puntos específicos a lo largo de una trayectoria. Esta trayectoria puede ser una línea recta en un eje cartesiano, o bien un camino curvo. La distancia se calcula midiendo la longitud de la trayectoria entre los dos puntos de partida y llegada.
ID:(9495, 0)
Tiempo
Ejercicio 
La evolución de cualquier sistema se describe mediante distintos parámetros, cada uno de ellos evolucionando en función de un escalar denominado el tiempo ($t$).

Tradicionalmente, el tiempo se consideraba absoluto en la física clásica, siendo igual en todos los sistemas de referencia. No obstante, la teoría de la relatividad ha generalizado este concepto y ahora debe ser visto como propio de cada sistema de referencia, pudiendo diferir en su avance.
ID:(478, 0)
Tiempo inicial
Ecuación 
De esta forma, podemos fijar el tiempo inicial ($t_0$) según sea más conveniente para facilitar los cálculos. Esto puede ser hecho en función del instrumento con que se determina el tiempo, para asegurar la precisión de los resultados, o de manera teórica para simplificar los cálculos.
De esta forma, el tiempo inicial puede ser fijado libremente sin preocuparse por cambios en el resultado.
ID:(715, 0)
Tiempo transcurrido
Script 
La base de la descripción de cualquier evolución es la definición del tiempo en que se describe. En particular, se trabaja con el tiempo transcurrido ($\Delta t$) desde un tiempo de referencia.

• En el caso de un cronómetro, el tiempo transcurrido se mide desde el inicio de su medición, es decir, un tiempo inicial cero ($t_0=0$).
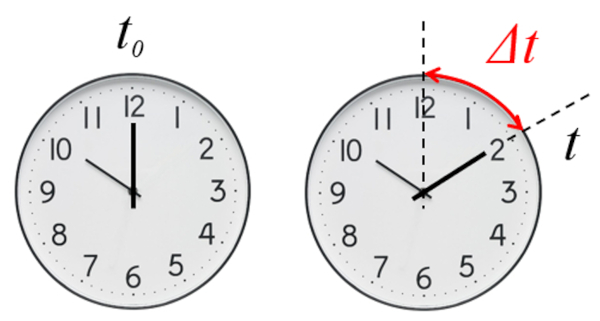
• En el caso de un reloj, el tiempo transcurrido se mide desde un tiempo inicial definido, que puede ser o no cero.
ID:(12507, 0)
Velocidad media
Variable 
Para poder estimar cómo se desplaza un objeto debemos conocer el camino recorrido por tiempo. Por lo tanto, se introduce la proporción entre el camino recorrido y el tiempo transcurrido, que se define como la velocidad media.
Para medir la velocidad media se puede utilizar un sistema como el que se muestra en la imagen:
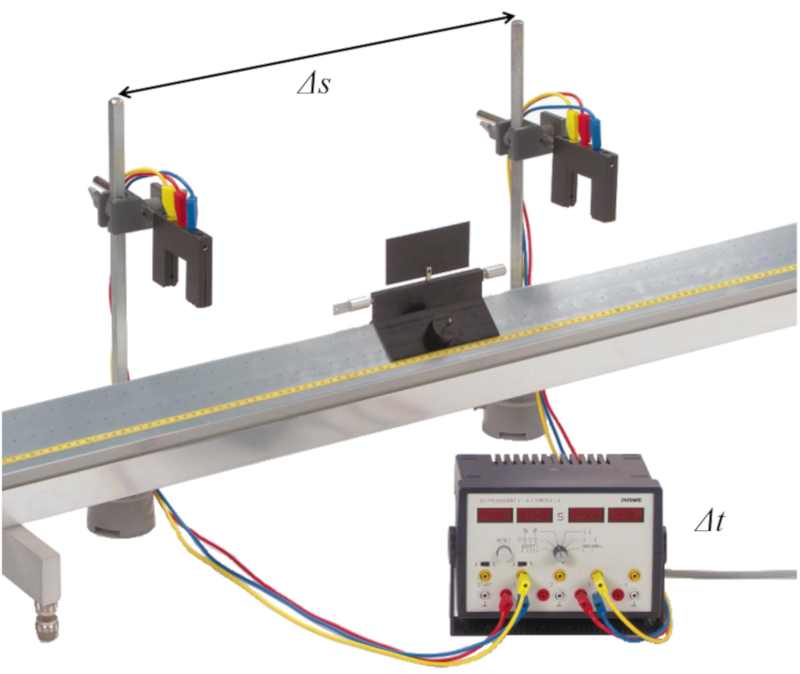
Para determinar la velocidad media, se deben colocar dos sensores que registren el paso de un objeto a una distancia $\Delta s$. Luego, se registra la diferencia de tiempos en que el objeto pasa frente a cada sensor $\Delta t$. Con ambos valores se determina la velocidad media dividiendo la distancia recorrida por el tiempo transcurrido.
La ecuación que describe la la velocidad media ($\bar{v}$) con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) es la siguiente:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Es importante tener en cuenta que la velocidad media es solo una estimación de la velocidad real. El principal problema radica en que:
Si la velocidad varía durante el tiempo transcurrido, el valor de la velocidad media puede ser muy diferente a la velocidad promedio.
Además, existe un problema en la forma en que se mide la distancia recorrida, ya que se trabaja con dos posiciones. Esto puede llevar a que:
Como el camino recorrido se calcula a partir de la diferencia de dos posiciones, puede darse el caso de que el movimiento se invierta durante el tiempo transcurrido, y que la posición inicial y final sean muy similares. Esto puede resultar en una velocidad media aproximadamente nula, aunque se haya recorrido un camino largo.
Por lo tanto, la clave es:
Determinar la velocidad en un intervalo de tiempo suficientemente corto, de modo que su variación sea mínima.
ID:(470, 0)
Velocidad como pendiente de la curva posición
Audio 
Si se representa el desplazamiento como una recta entre el origen O y el punto A:
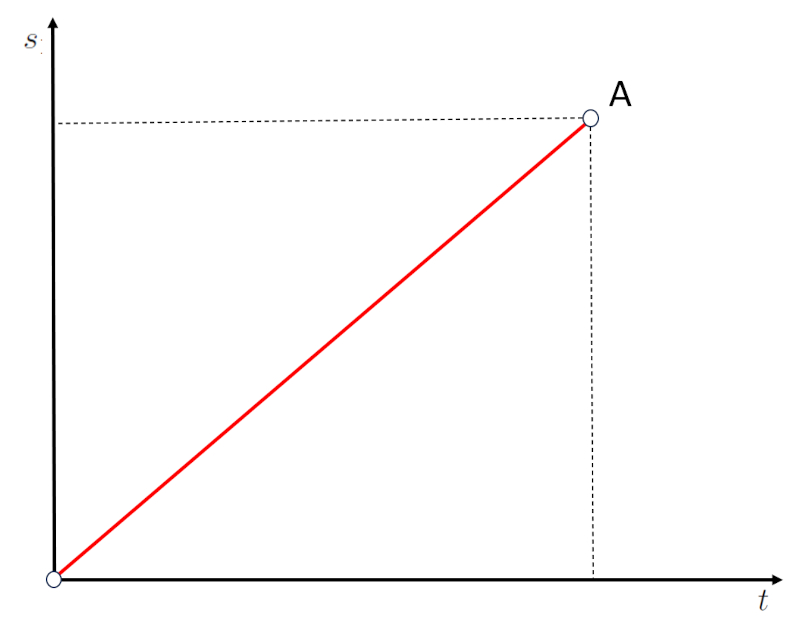
Diagrama posición-tiempo
se observa que se ha recorrido una distancia en un tiempo transcurrido. Por lo tanto, la pendiente de la gráfica distancia vs tiempo transcurrido corresponde a la velocidad.
Si la pendiente es mayor, significa que se ha recorrido una mayor distancia en un tiempo menor, lo que corresponde a una velocidad mayor.
Si la pendiente es menor, significa que se ha recorrido una menor distancia en un tiempo mayor, lo que corresponde a una velocidad menor.
ID:(2239, 0)
Diagrama camino tiempo con segmento horizontal
Video 
Un segundo tipo de caso son segmentos horizontales en el diagrama camino vs tiempo:
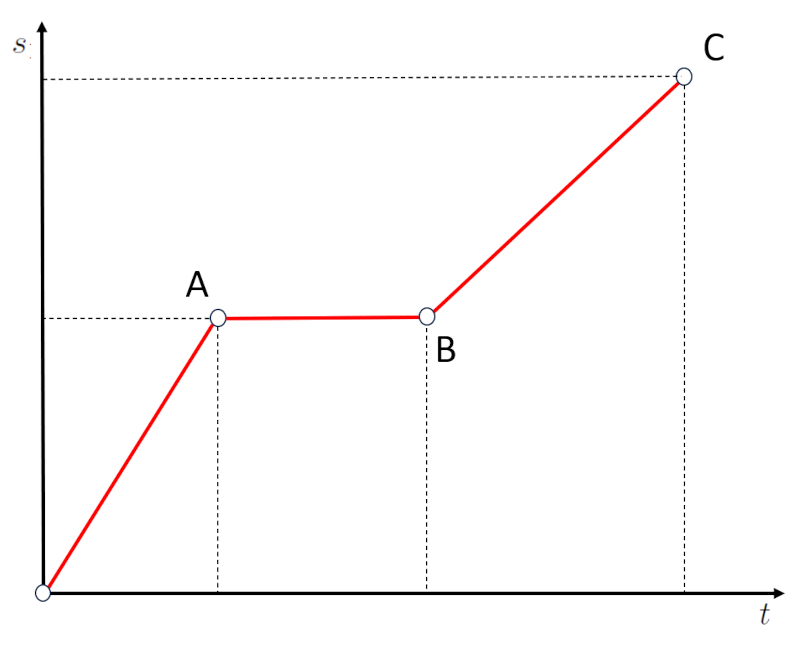
Si observamos el segmento AB notaremos que pese a que ha transcurrido tiempo el camino no ha variado. Esto significa que el objeto esta detenido. Por ello segmentos horizontales, que corresponden a una pendiente nula, corresponde a etapas en que la velocidad es nula.
ID:(2241, 0)
Gráfica camino tiempo para velocidad constante y tiempo inicial
Unidad 
Para el caso de velocidad constante y tiempo inicial, la posición puede calcularse utilizando los valores la posición ($s$), la posición inicial ($s_0$), la velocidad constante ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) mediante la siguiente ecuación:
| $ s = s_0 + v_0 ( t - t_0 )$ |
que corresponde a una recta con:
• una pendiente igual a la velocidad constante ($v_0$)
• un punto de corte en la posición inicial ($s_0$) para el tiempo inicial ($t_0$)
que se muestra a continuación:
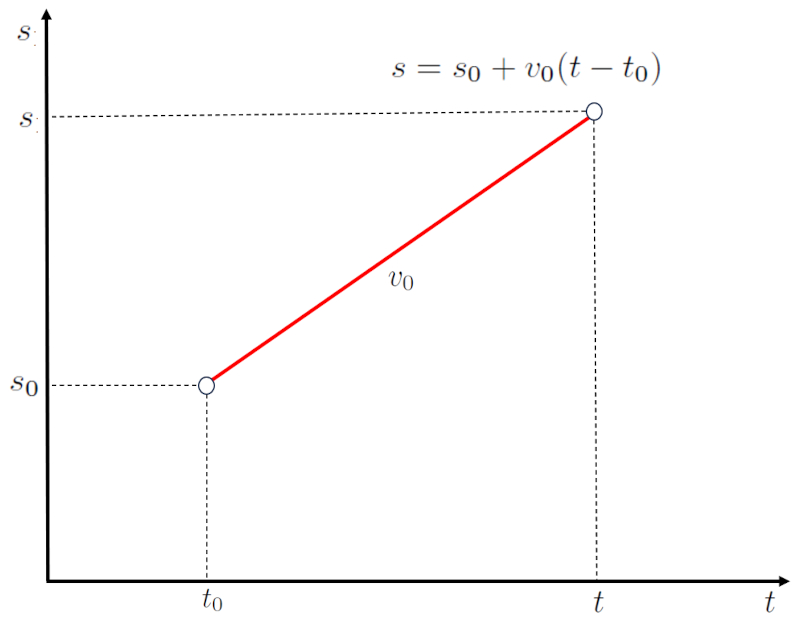
ID:(2243, 0)
Pendiente negativa
Code 
En el caso de la gráfica en la que un segmento tiene pendiente negativa:
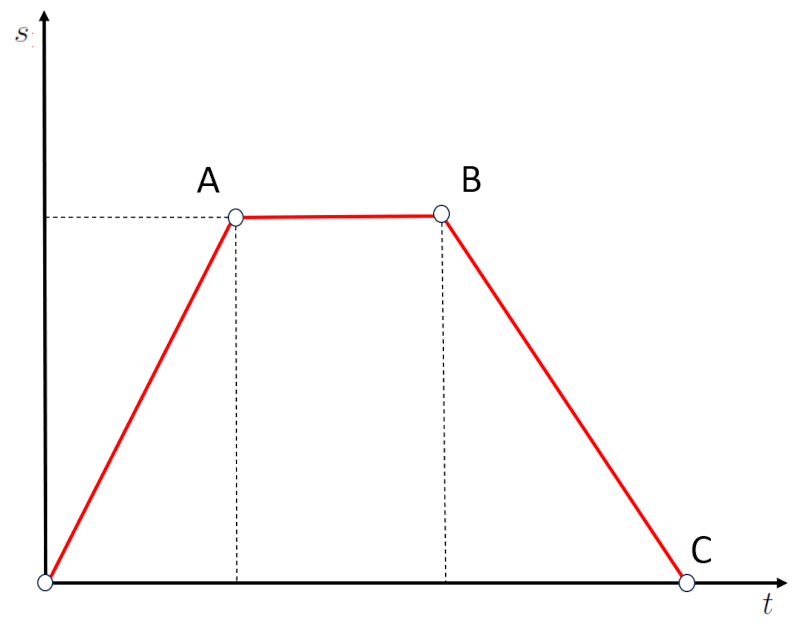
presenta una situación en la que se regresó de la posición B a C, la cual se encuentra a una distancia nula. En otras palabras, las pendientes negativas corresponden a viajar en dirección opuesta, no alejándose, sino acercándose al origen.
ID:(2245, 0)
Paradoja del cuerpo en reposo
Flujo 
Si un objeto se encuentra en "reposo", esto significa que está en reposo en relación a nuestro sistema de referencia o sistema de coordenadas. Sin embargo, este "reposo" es totalmente relativo. Es decir, desde el punto de vista de un objeto que se mueve con respecto a nuestro sistema, el objeto en "reposo" también está en movimiento.
En este sentido, no existe un "objeto en reposo" como algo absoluto, sino que es relativo a un sistema de referencia particular. Por lo tanto, en general, todas las mediciones de velocidad se realizan en relación a un sistema de referencia específico.
Por ejemplo, si un objeto parece desplazarse muy lentamente, esto solo significa que su velocidad es muy similar a la velocidad del sistema de referencia en el que se observa el movimiento lento.
ID:(4405, 0)
Modelo
Matriz 
El modelo base relaciona la posición ($s$), medido desde un origen la posición inicial ($s_0$), lo que resulta en una distancia recorrida en un tiempo ($\Delta s$), y el tiempo ($t$), medido desde un origen el tiempo inicial ($t_0$), lo que da el tiempo transcurrido ($\Delta t$). A partir de estas diferencias, se define la velocidad media ($\bar{v}$), que si se asume constante, se iguala a la velocidad constante ($v_0$).
La relación base del modelo es la recta que asocia las variables centrales del modelo:

Con esto, la estructura de red del modelo es la siguiente:
ID:(15378, 0)
Velocidad constante
Descripción 
Para describir cómo evoluciona la posición en el tiempo, es necesario analizar la variación de ésta a lo largo del tiempo.
La relación entre la variación de la posición equivale a la distancia recorrida en el tiempo transcurrido, que, al dividirla por dicho tiempo, se convierte en la velocidad.
Variables
Cálculos
Cálculos
Ecuaciones
Con la distancia recorrida en un tiempo ($\Delta s$) es con la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s = s_2 - s_1 $ |
y el tiempo transcurrido ($\Delta t$) es con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Se tiene que la ecuaci n de la velocidad media:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
puede escribirse como:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
Por lo tanto, despejando, se obtiene:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Ejemplos
Cuando un objeto se desplaza a velocidad constante, recorre distancias iguales en intervalos de tiempo iguales. En este caso, la posici n var a de forma lineal con el tiempo transcurrido.
Para comprender este modelo, ejecute la simulaci n con el bot n Start y det ngala con Stop. Luego, observe los valores indicados en la regla inferior: la distancia recorrida en un tiempo ($\Delta s$), y en el cron metro: el tiempo transcurrido ($\Delta t$). Al dividir el primero por el segundo, obtendr la velocidad la velocidad constante ($v_0$) ingresada.
(ID 15379)
La posición ($s$) de un objeto en un sistema unidimensional se refiere a la ubicaci n del objeto en relaci n con un punto de referencia. Esta ubicaci n se expresa como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una l nea recta en un eje cartesiano, o puede seguir un camino curvo:

Posici n a lo largo de una carretera siguiendo el eje de esta
(ID 15)
La posición inicial ($s_0$) es la ubicaci n inicial de un objeto antes de que comience un movimiento. Esta ubicaci n se define como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una l nea recta sobre un eje cartesiano, o puede seguir una trayectoria curva.

Posici n inicial a lo largo de una carretera siguiendo el eje de esta
(ID 10302)
La distancia recorrida en un tiempo ($\Delta s$) por un objeto se determina midiendo la distancia entre dos puntos espec ficos a lo largo de una trayectoria. Esta trayectoria puede ser una l nea recta en un eje cartesiano o un camino curvo. La distancia se calcula como la longitud de la trayectoria que conecta los dos puntos inicial y final.

Distancia recorrida desde un punto inicial hasta un punto final
Como el valor de la distancia recorrida en un tiempo ($\Delta s$) se calcula como la diferencia entre la posición ($s$) y la posición inicial ($s_0$):
| $ \Delta s = s_2 - s_1 $ |
es posible "trasladar" el origen de la posici n a adiendo un valor constante $d$ a ambas magnitudes:
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
sin afectar el resultado de la distancia recorrida:
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
Este concepto se conoce como invariancia espacial, lo que implica que el valor de la distancia recorrida no depende del punto espec fico desde el cual se inicia la medici n.
Esto significa que las leyes formuladas utilizando este principio ser n invariantes espaciales, es decir, ser n v lidas independientemente del lugar donde se realice la medici n.
(ID 9495)
La evoluci n de cualquier sistema se describe mediante distintos par metros, cada uno de ellos evolucionando en funci n de un escalar denominado el tiempo ($t$).
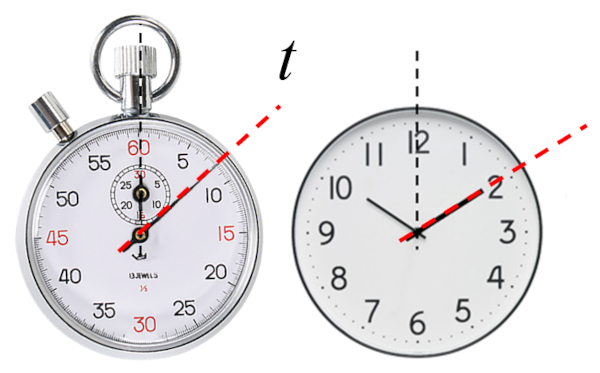
Tiempo que indica un reloj ya sea el valor en que se marca o la hora
Tradicionalmente, el tiempo se consideraba absoluto en la f sica cl sica, siendo igual en todos los sistemas de referencia. No obstante, la teor a de la relatividad ha generalizado este concepto y ahora debe ser visto como propio de cada sistema de referencia, pudiendo diferir en su avance.
(ID 478)
De esta forma, podemos fijar el tiempo inicial ($t_0$) seg n sea m s conveniente para facilitar los c lculos. Esto puede ser hecho en funci n del instrumento con que se determina el tiempo, para asegurar la precisi n de los resultados, o de manera te rica para simplificar los c lculos.
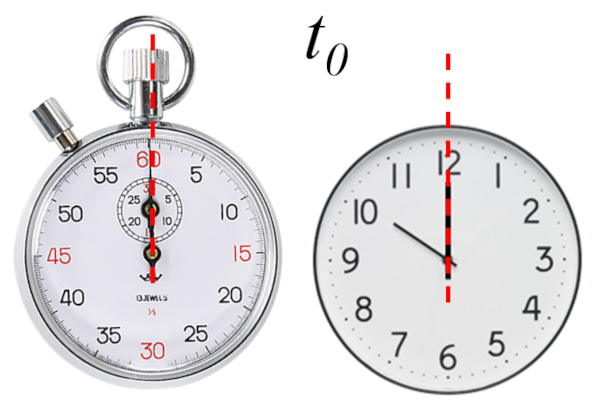
El tiempo en que se inicia la medici n ya sea fijado o por sistema (cron metro)
De esta forma, el tiempo inicial puede ser fijado libremente sin preocuparse por cambios en el resultado.
(ID 715)
La base de la descripci n de cualquier evoluci n es la definici n del tiempo en que se describe. En particular, se trabaja con el tiempo transcurrido ($\Delta t$) desde un tiempo de referencia.
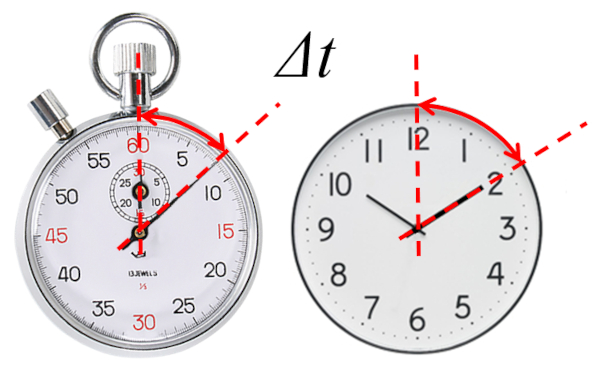
El cronometro nos entre directamente el tiempo transcurrido ya que su tiempo inicial es nulo
En el caso de un cron metro, el tiempo transcurrido se mide desde el inicio de su medici n, es decir, un tiempo inicial cero ($t_0=0$).

En el caso del reloj es necesario definir el tipo inicial para poder determinar el tiempo trascurrido.
En el caso de un reloj, el tiempo transcurrido se mide desde un tiempo inicial definido, que puede ser o no cero.
Como el tiempo transcurrido ($\Delta t$) se calcula como la diferencia entre el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
es posible "trasladar" el origen del tiempo sumando un valor constante
a ambas magnitudes:
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
sin afectar el resultado del tiempo transcurrido:
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
Este concepto se conoce como invariancia temporal, lo que implica que el valor del tiempo transcurrido no depende del momento espec fico en que se inicia la medici n.
Esto significa que las leyes formuladas utilizando este principio ser n invariantes temporales, es decir, ser n v lidas independientemente de si se aplican en el presente, en el pasado o en el futuro.
(ID 12507)
Para poder estimar c mo se desplaza un objeto debemos conocer el camino recorrido por tiempo. Por lo tanto, se introduce la proporci n entre el camino recorrido y el tiempo transcurrido, que se define como la velocidad media.
Para medir la velocidad media se puede utilizar un sistema como el que se muestra en la imagen:

Para determinar la velocidad media, se deben colocar dos sensores que registren el paso de un objeto a una distancia $\Delta s$. Luego, se registra la diferencia de tiempos en que el objeto pasa frente a cada sensor $\Delta t$. Con ambos valores se determina la velocidad media dividiendo la distancia recorrida por el tiempo transcurrido.
La ecuaci n que describe la la velocidad media ($\bar{v}$) con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) es la siguiente:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Es importante tener en cuenta que la velocidad media es solo una estimaci n de la velocidad real. El principal problema radica en que:
Si la velocidad var a durante el tiempo transcurrido, el valor de la velocidad media puede ser muy diferente a la velocidad promedio.
Adem s, existe un problema en la forma en que se mide la distancia recorrida, ya que se trabaja con dos posiciones. Esto puede llevar a que:
Como el camino recorrido se calcula a partir de la diferencia de dos posiciones, puede darse el caso de que el movimiento se invierta durante el tiempo transcurrido, y que la posici n inicial y final sean muy similares. Esto puede resultar en una velocidad media aproximadamente nula, aunque se haya recorrido un camino largo.
Por lo tanto, la clave es:
Determinar la velocidad en un intervalo de tiempo suficientemente corto, de modo que su variaci n sea m nima.
(ID 470)
Si se representa el desplazamiento como una recta entre el origen O y el punto A:

Diagrama posici n-tiempo
se observa que se ha recorrido una distancia en un tiempo transcurrido. Por lo tanto, la pendiente de la gr fica distancia vs tiempo transcurrido corresponde a la velocidad.
Si la pendiente es mayor, significa que se ha recorrido una mayor distancia en un tiempo menor, lo que corresponde a una velocidad mayor.
Si la pendiente es menor, significa que se ha recorrido una menor distancia en un tiempo mayor, lo que corresponde a una velocidad menor.
(ID 2239)
Un segundo tipo de caso son segmentos horizontales en el diagrama camino vs tiempo:

Si observamos el segmento AB notaremos que pese a que ha transcurrido tiempo el camino no ha variado. Esto significa que el objeto esta detenido. Por ello segmentos horizontales, que corresponden a una pendiente nula, corresponde a etapas en que la velocidad es nula.
(ID 2241)
Para el caso de velocidad constante y tiempo inicial, la posici n puede calcularse utilizando los valores la posición ($s$), la posición inicial ($s_0$), la velocidad constante ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) mediante la siguiente ecuaci n:
| $ s = s_0 + v_0 ( t - t_0 )$ |
que corresponde a una recta con:
• una pendiente igual a la velocidad constante ($v_0$)
• un punto de corte en la posición inicial ($s_0$) para el tiempo inicial ($t_0$)
que se muestra a continuaci n:

(ID 2243)
En el caso de la gr fica en la que un segmento tiene pendiente negativa:

presenta una situaci n en la que se regres de la posici n B a C, la cual se encuentra a una distancia nula. En otras palabras, las pendientes negativas corresponden a viajar en direcci n opuesta, no alej ndose, sino acerc ndose al origen.
(ID 2245)
Si un objeto se encuentra en "reposo", esto significa que est en reposo en relaci n a nuestro sistema de referencia o sistema de coordenadas. Sin embargo, este "reposo" es totalmente relativo. Es decir, desde el punto de vista de un objeto que se mueve con respecto a nuestro sistema, el objeto en "reposo" tambi n est en movimiento.
En este sentido, no existe un "objeto en reposo" como algo absoluto, sino que es relativo a un sistema de referencia particular. Por lo tanto, en general, todas las mediciones de velocidad se realizan en relaci n a un sistema de referencia espec fico.
Por ejemplo, si un objeto parece desplazarse muy lentamente, esto solo significa que su velocidad es muy similar a la velocidad del sistema de referencia en el que se observa el movimiento lento.
(ID 4405)
El modelo base relaciona la posición ($s$), medido desde un origen la posición inicial ($s_0$), lo que resulta en una distancia recorrida en un tiempo ($\Delta s$), y el tiempo ($t$), medido desde un origen el tiempo inicial ($t_0$), lo que da el tiempo transcurrido ($\Delta t$). A partir de estas diferencias, se define la velocidad media ($\bar{v}$), que si se asume constante, se iguala a la velocidad constante ($v_0$).
La relaci n base del modelo es la recta que asocia las variables centrales del modelo:

Con esto, la estructura de red del modelo es la siguiente:
(ID 15378)
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuaci n:
| $ \Delta s = s_2 - s_1 $ |
(ID 4352)
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:
| $ \Delta t \equiv t - t_0 $ |
(ID 4353)
La velocidad media ($\bar{v}$) se puede calcular de la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$) mediante:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
(ID 3152)
Si la velocidad es constante, la velocidad ser igual a la velocidad inicial ($v_0$). En este caso, el camino recorrido en funci n del tiempo puede calcularse utilizando la diferencia entre la posición ($s$) y la posición inicial ($s_0$), dividida por la diferencia entre el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )$ |
La ecuaci n correspondiente define una l nea recta en el espacio-tiempo.
(ID 3154)
ID:(608, 0)
