Aceleración constante
Storyboard 
Para que un objeto alcance una velocidad determinada, primero debe aumentar su velocidad desde el reposo. Este proceso se denomina aceleración y se define en función de la variación de la velocidad en el tiempo. Por otro lado, si se busca reducir la velocidad e incluso detener el objeto, también se introduce una aceleración, pero con el signo opuesto al de la velocidad (si la velocidad es positiva, la aceleración es negativa, y viceversa), lo que se conoce como frenado.
ID:(609, 0)
Aceleración constante
Storyboard 
Para que un objeto alcance una velocidad determinada, primero debe aumentar su velocidad desde el reposo. Este proceso se denomina aceleración y se define en función de la variación de la velocidad en el tiempo. Por otro lado, si se busca reducir la velocidad e incluso detener el objeto, también se introduce una aceleración, pero con el signo opuesto al de la velocidad (si la velocidad es positiva, la aceleración es negativa, y viceversa), lo que se conoce como frenado.
Variables
Cálculos
Cálculos
Ecuaciones
En el caso de que la aceleración constante ($a_0$) sea igual a la aceleración media ($\bar{a}$), ser igual a
Por lo tanto, considerando la diferencia de velocidad ($\Delta v$)
y el tiempo transcurrido ($\Delta t$)
la ecuaci n de la aceleración constante ($a_0$)
se puede escribir como
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
y al despejar, se obtiene
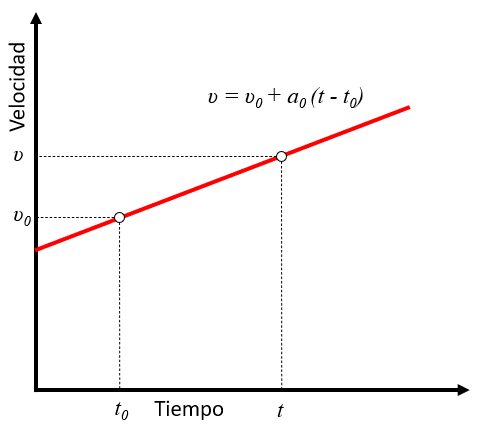
En el caso de la aceleración constante ($a_0$), la velocidad ($v$) en funci n de el tiempo ($t$) es una recta que pasa por el tiempo inicial ($t_0$) y la velocidad inicial ($v_0$), definida por la ecuaci n:
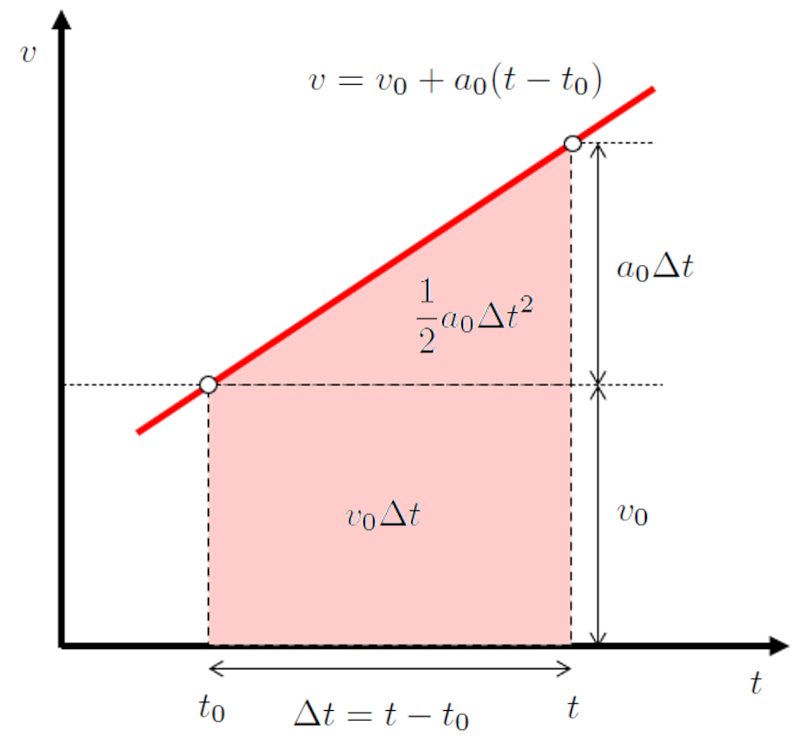
Dado que la distancia recorrida en un tiempo ($\Delta s$) representa el rea bajo la curva velocidad-tiempo, podemos sumar las contribuciones del rect ngulo:
$v_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Para obtener la distancia recorrida en un tiempo ($\Delta s$) con la posición ($s$) y la posición inicial ($s_0$), resultando en:
Por lo tanto:
Si despejamos las ecuaciones para el tiempo ($t$) y el tiempo inicial ($t_0$) en la ecuaci n de la velocidad ($v$), que depende de la velocidad inicial ($v_0$) y la aceleración constante ($a_0$):
obtenemos:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Y al sustituir esto en la ecuaci n de la posición ($s$) con la posición inicial ($s_0$):
obtenemos una expresi n para el camino recorrido en funci n de la velocidad:
La definici n de la aceleración media ($\bar{a}$) se considera como la relaci n entre la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$). Es decir,
y
Se define la relaci n entre ambos como la aceleración centrifuga ($a_c$)
en dicho intervalo de tiempo.
Ejemplos
La estructura general del modelo de la aceleración constante ($a_0$) en que por un lado se iguala a la aceleración media ($\bar{a}$) y con ello la relaci n entre la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$).
Por otro lado existe tres relaciones en torno a la aceleración constante ($a_0$) en que se asocia a la velocidad ($v$) y el tiempo ($t$) ($v, t$), a la posición ($s$) y el tiempo ($t$) ($s, t$) o la posición ($s$) y la velocidad ($v$) ($s, v$):
Por ltimo las relaciones se asocian a par metros que no se muestran que son la posición inicial ($s_0$), la velocidad inicial ($v_0$) y el tiempo inicial ($t_0$) y que seg n el sistema de coordenadas que se emplea pueden ser definidas como nulas. Esto es iniciar el movimiento en el origen ($s_0=0$), comenzar a medir desde el origen del tiempo ($t_0=0$) y el origen del sistema de coordenadas est en reposo respecto del observador por lo que no hay velocidad inicial ($v_0=0$).
Cuando la velocidad no es constante, es importante conocer c mo va aumentando o disminuyendo. Para ello, es necesario conocer la tasa de cambio de la velocidad por unidad de tiempo, que se conoce como aceleraci n o desaceleraci n, seg n se trate de un aumento o una disminuci n de la velocidad.
Por ejemplo, si viajamos a una velocidad de 100 km/h y frenamos reduciendo la velocidad en 10 km/h por segundo, sabemos que nos detendremos en 10 segundos.
La aceleraci n se basa en la medici n de la variaci n de la velocidad y la variaci n del tiempo.
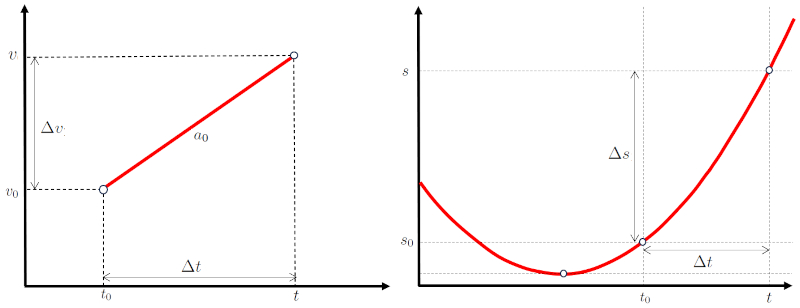
Cuando la aceleraci n es constante, la variaci n de la velocidad, representada por la velocidad ($v$), cambia linealmente en funci n de el tiempo ($t$). Esto se puede calcular utilizando la velocidad inicial ($v_0$), la aceleración constante ($a_0$) y el tiempo inicial ($t_0$), lo que nos da la ecuaci n:
Esta relaci n se representa gr ficamente como una l nea recta, como se muestra a continuaci n:
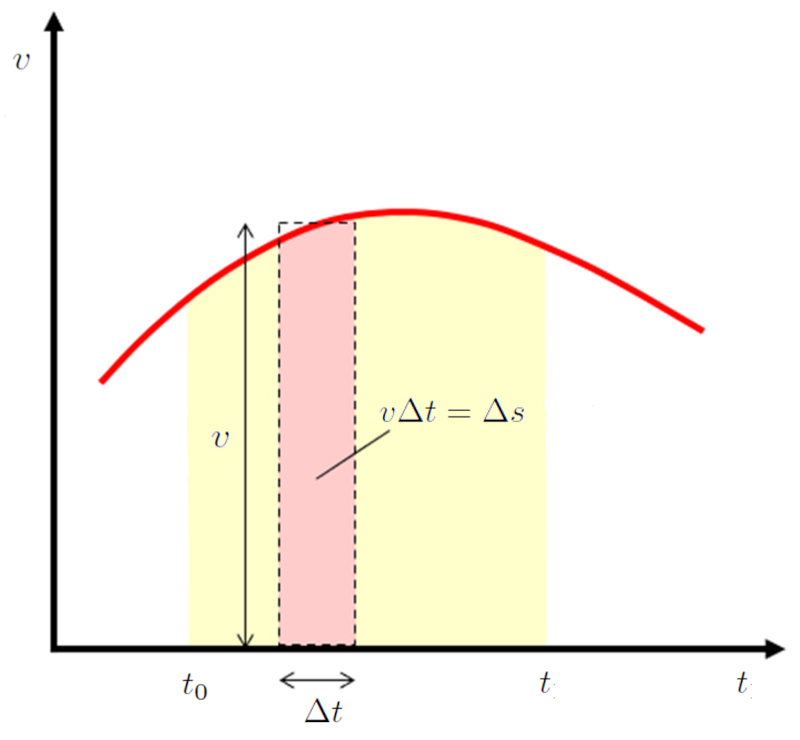
Si consideramos un rea de ancho $\Delta t$ en un gr fico de velocidad versus tiempo, podemos ver que corresponde al desplazamiento durante ese tiempo:
En el caso particular donde la aceleraci n es constante, la velocidad se representa en el gr fico de velocidad versus tiempo como una recta. Esta recta est definida por la velocidad ($v$), la velocidad inicial ($v_0$), la aceleración constante ($a_0$), el tiempo ($t$) y el tiempo inicial ($t_0$), igual a:
y se grafica como sigue:
Dado que el rea debajo de la curva se puede representar como la suma de un rect ngulo de rea
$v_0(t-t_0)$
y un tri ngulo de rea
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Podemos calcular el desplazamiento la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición ($s$) y la posición inicial ($s_0$), lo que nos lleva a:
Por lo tanto, la posición ($s$) es igual a:
Si despejamos la ecuaci n de la velocidad ($v$) para la aceleración constante ($a_0$) en funci n de la velocidad inicial ($v_0$) y el tiempo inicial ($t_0$):
y lo sustituimos en la ecuaci n de la posición ($s$) con la posición inicial ($s_0$):
obtenemos la expresi n para el camino en funci n de la velocidad:
De esta relaci n, podemos observar que tanto el camino de aceleraci n como el de frenado dependen del cuadrado de la velocidad final/inicial. Es decir, duplicar la velocidad requerir a un camino cuatro veces m s largo.
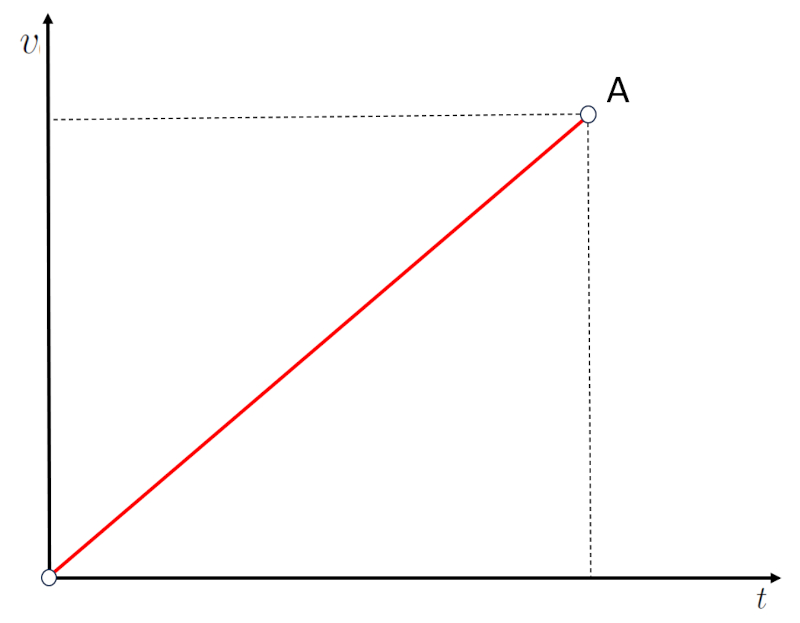
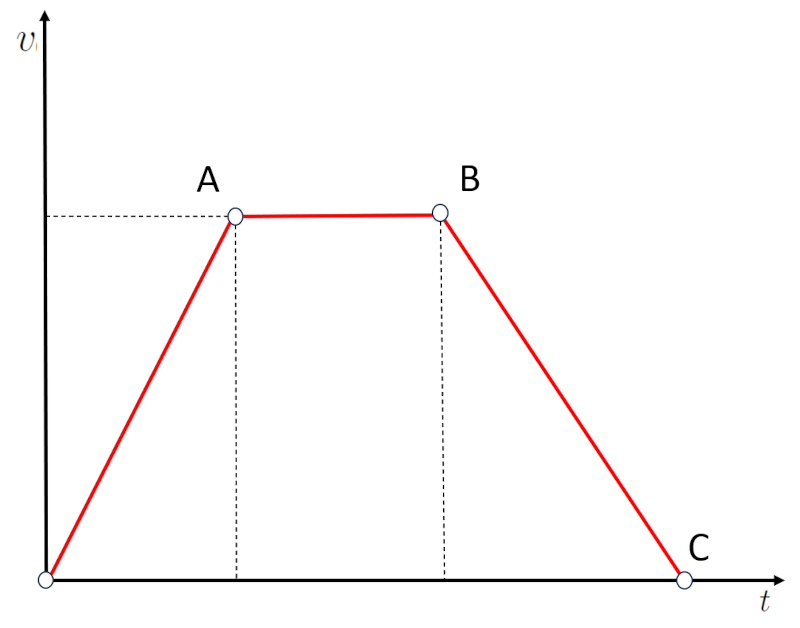
Si se representa gr ficamente la velocidad como una recta entre la velocidad inicial en O y la velocidad final en A:
Se puede observar que la velocidad ha aumentado durante el tiempo transcurrido. Por lo tanto, la pendiente de la gr fica de velocidad vs. tiempo corresponde a la aceleraci n.
Cuanto mayor sea la pendiente, mayor ser el aumento de la velocidad en un menor tiempo, lo que se corresponde con una mayor aceleraci n.
Por el contrario, si la pendiente es menor, significa que la velocidad ha aumentado en un mayor tiempo, lo que corresponde a una menor aceleraci n.
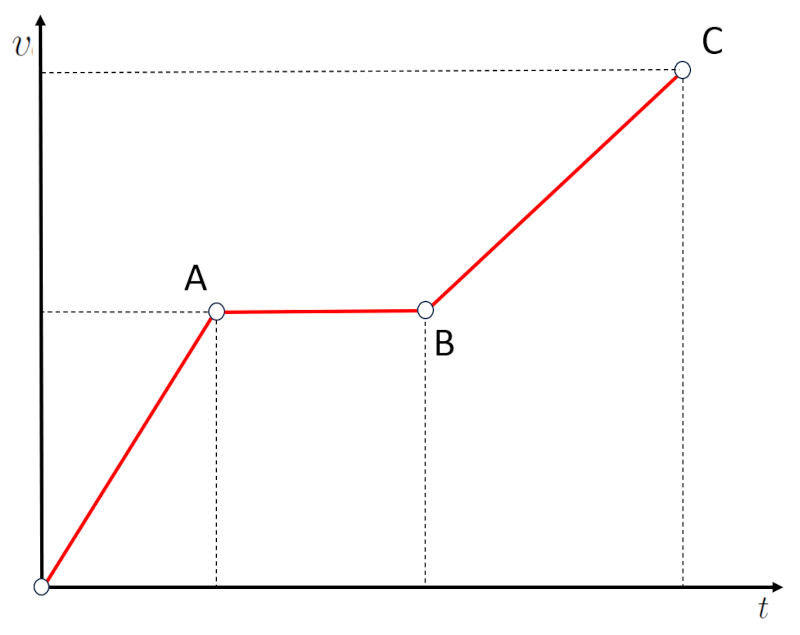
Un tipo de escenario en el gr fico de velocidad vs tiempo es cuando hay segmentos horizontales:
Si observamos el segmento AB, podemos ver que a pesar del paso del tiempo, la velocidad no ha cambiado. Esto significa que el objeto est viajando con velocidad constante (cuidado, esto NO significa que se haya detenido). Por lo tanto, los segmentos horizontales, que corresponden a una pendiente nula, corresponden a etapas donde la aceleraci n es cero.
En el caso de la gr fica en la que un segmento tiene pendiente negativa:
se presenta una situaci n en la que la velocidad se reduce entre B y C volviendo al valor cero. En otras palabras, las pendientes negativas corresponden, en este caso, a un proceso de frenado.
Para velocidades positivas, las pendientes negativas corresponden a un proceso de frenado. Sin embargo, para velocidades negativas, una pendiente negativa corresponde a un incremento de la velocidad negativa y, por lo tanto, a una aceleraci n. En el caso de velocidades negativas, la aceleraci n positiva corresponde a un proceso de frenado.
Un proceso de frenado es aquel cuya aceleraci n tiene un signo opuesto al de la velocidad.
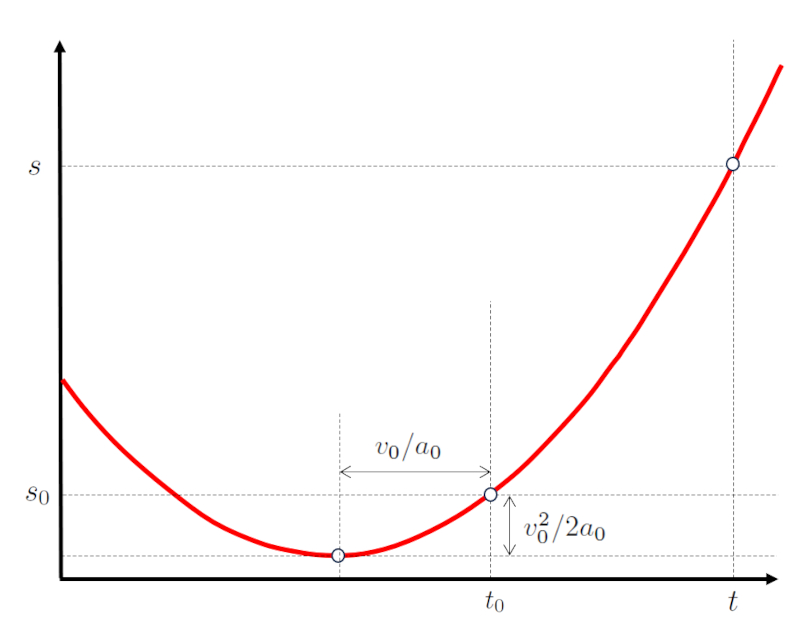
Para el caso de la aceleración constante ($a_0$), la posición ($s$) es una funci n de el tiempo ($t$) expresada en t rminos de la velocidad inicial ($v_0$), la posición inicial ($s_0$) y el tiempo inicial ($t_0$):
que corresponde a una par bola:
La par bola es normal si la aceleraci n es positiva ($a_0>0$) e invertida si es negativa ($a_0<0$).
Si $v_0/a_0$ es positivo, el m nimo ($a_0>0$) o m ximo ($a_0<0$) se produce antes del tiempo inicial, por lo que la evoluci n no mostrar un cambio de signo en la velocidad, ya que la pendiente de la curva no cambia de signo.
Si $v_0/a_0$ es negativo, el m nimo ($a_0>0$) o m ximo ($a_0<0$) se produce despu s del tiempo inicial, lo que resultar en una inversi n del movimiento en el futuro.
En el caso de ser un m nimo ($a_0>0$), este se encuentra en una posici n inferior a la posici n inicial a una distancia $v_0^2/2a_0$. De manera similar, si es un m ximo ($a_0<0$), se ubicar en una posici n superior a la posici n inicial a una distancia $v_0^2/2a_0$.
Una situaci n com n es que la aceleraci n sea constante, lo que significa que la velocidad aumenta proporcionalmente al tiempo transcurrido.
Por lo tanto la aceleración constante ($a_0$),
$a_0=g$
Un ejemplo de aceleraci n constante es la aceleraci n de la gravedad que experimentan los objetos al caer sobre la superficie del planeta. En la superficie de la Tierra, esta aceleraci n es de $9,8 m/s^2$ y generalmente se denota con la letra $g$. De hecho, existe una unidad de medida llamada $g$ que equivale a $9,8 m/s^2$.
Un cuerpo que se desplaza a una velocidad constante no experimenta aceleraci n.
Por lo tanto, en el caso en que la aceleración constante ($a_0$) sea nulo,
$a_0=0$
la posición ($s$), con la posición inicial ($s_0$), la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$),
se reduce al caso de velocidad constante:
Si igualamos la aceleración constante ($a_0$) y la aceleración media ($\bar{a}$), asociamos la definici n de la aceleración media ($\bar{a}$) con la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$).
Por otro lado, consideramos la recta que permite calcular la velocidad ($v$) en funci n de la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$).
Usando la relaci n de la velocidad, podemos calcular la posición ($s$) en funci n de la posición inicial ($s_0$), la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$), o en funci n de la posición inicial ($s_0$), la velocidad ($v$) y la velocidad inicial ($v_0$).
Ambas ecuaciones incluyen la aceleración constante ($a_0$). Finalmente, incorporamos la distancia recorrida en un tiempo ($\Delta s$), el tiempo transcurrido ($\Delta t$) y la diferencia de velocidad ($\Delta v$), donde restamos el valor final del valor inicial.
Estas relaciones se representan en el siguiente gr fico:
Las ecuaciones que cumplen estas relaciones dan lugar al siguiente modelo que permite calcular cualquier escenario:
La aceleraci n se define como la variaci n de la velocidad por unidad de tiempo.
Por lo tanto, es necesario establecer la diferencia de velocidad ($\Delta v$) en funci n de la velocidad ($v$) y la velocidad inicial ($v_0$) de la siguiente manera:
Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duraci n se determina restando el tiempo inicial al tiempo final:
La proporci n en la que la variaci n de la velocidad a lo largo del tiempo se define como la aceleración media ($\bar{a}$). Para medirla, es necesario observar la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$).
Un m todo com n para medir la aceleraci n media consiste en utilizar una l mpara estrobosc pica que ilumina el objeto en intervalos definidos. Al tomar una fotograf a, se puede determinar la distancia recorrida por el objeto en ese tiempo. Al calcular dos velocidades consecutivas, se puede determinar su variaci n y, con el tiempo transcurrido entre las fotos, la aceleraci n media.
La ecuaci n que describe la aceleraci n media es la siguiente:
Es importante tener en cuenta que la aceleraci n media es una estimaci n de la aceleraci n real.
El problema principal radica en que si la aceleraci n var a durante el tiempo transcurrido, el valor de la aceleraci n media puede diferir en gran medida de la aceleraci n promedio
.
Por lo tanto, la clave es
Determinar la aceleraci n en un per odo de tiempo suficientemente corto para minimizar la variaci n.
Si la aceleración constante ($a_0$), entonces la aceleración media ($\bar{a}$) es igual al valor de la aceleraci n, es decir,
En este caso, la velocidad ($v$) como funci n de el tiempo ($t$) se puede calcular recordando que est asociada con la diferencia entre la velocidad ($v$) y la velocidad inicial ($v_0$), as como el tiempo ($t$) y el tiempo inicial ($t_0$).
De esta manera, la ecuaci n representa una l nea recta en el espacio de velocidad-tiempo.
En el caso de que una aceleración constante ($a_0$), la variable la velocidad ($v$) var a de forma lineal con respecto a el tiempo ($t$), utilizando la velocidad inicial ($v_0$) y el tiempo inicial ($t_0$):
As , el rea bajo esta recta se puede calcular, lo que nos proporciona la distancia recorrida en un tiempo ($\Delta s$). Al combinar esto con la posición inicial ($s_0$), podemos calcular la posición ($s$), lo que resulta en:
Esto corresponde a la forma general de una par bola.
En el caso de una aceleraci n constante, podemos calcular la posición ($s$) a partir de la posición inicial ($s_0$), la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) seg n la ecuaci n:
Esto nos permite calcular la relaci n entre la distancia de aceleraci n/frenado y el cambio de velocidad:
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuaci n:
ID:(609, 0)