User:
Parallel currents
Image 
When two currents are allowed to flow in a parallel manner, we observe an attractive force between the wires.
It's worth recalling that currents consist of electrons in motion, and electrons naturally repel each other due to their negative charges. However, when these charges are in motion, this repulsive force turns into an attractive force, resulting in the observed attraction between the negatively charged conductors.
ID:(11772, 0)
Opposite parallel currents
Note
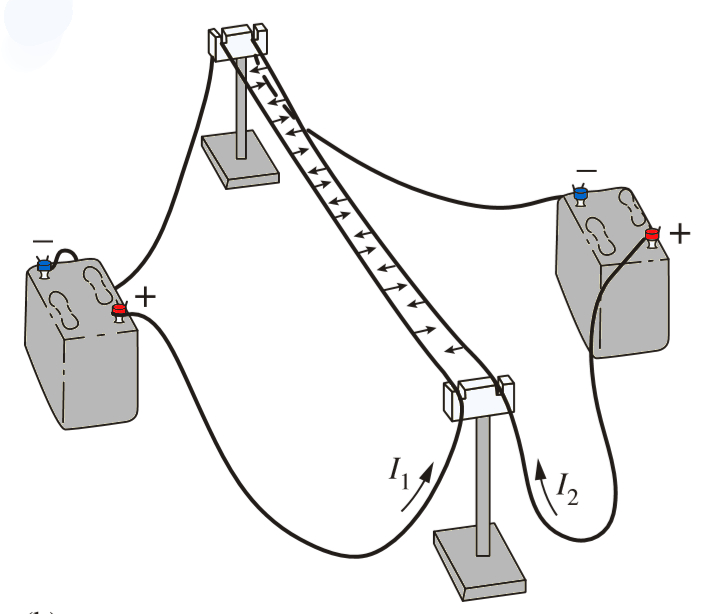
When two currents are allowed to flow in a parallel but opposite direction, we observe a repulsive force between the wires.
Comparing this experiment to the one where the flow is parallel but in the same direction, the key difference lies in the presence of relative velocity in the latter case.
ID:(11773, 0)
Wire interaction
Storyboard
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
Una alambre por el que circula corriente genera un campo magn tico circular en torno de este.
Por ello con
When considering a segment $dl$ of a wire with a certain cross-sectional area $S$ and length, it results in a volume of wire. Multiplying this volume by the charge density $c$ gives us the number of charges contained within it. Finally, by multiplying it by the unit charge $q$, we obtain the total charge present in the segment.
The current is defined by the equation:
and the charges within a segment of wire are represented by:
The ratio of the length of the segment to the corresponding time interval gives us the velocity:
$v =\displaystyle\frac{dl}{dt}$
Therefore, the current in the wire is equal to:
If a wire carrying a current $I_1$ generates a magnetic field given by:
This field generates a magnetic flux density represented by:
Which, in turn, produces a force per segment in a wire with a current $I_2$, defined as:
With this, the force per segment can be expressed as:
When two currents are allowed to flow in a parallel manner, we observe an attractive force between the wires.
It's worth recalling that currents consist of electrons in motion, and electrons naturally repel each other due to their negative charges. However, when these charges are in motion, this repulsive force turns into an attractive force, resulting in the observed attraction between the negatively charged conductors.
When two currents are allowed to flow in a parallel but opposite direction, we observe a repulsive force between the wires.
Comparing this experiment to the one where the flow is parallel but in the same direction, the key difference lies in the presence of relative velocity in the latter case.
ID:(1625, 0)