Benützer:
Parallelströme
Bild 
Wenn zwei Ströme in paralleler Weise fließen dürfen, beobachten wir eine anziehende Kraft zwischen den Leitungen.
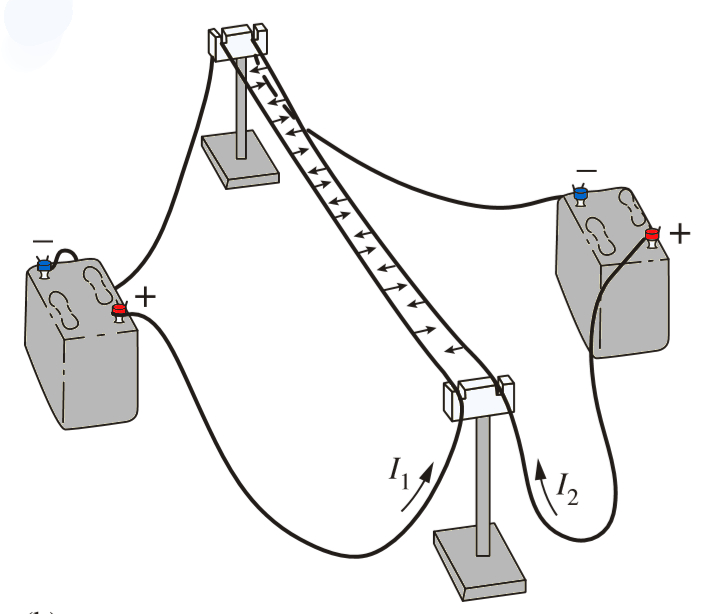
Es ist wichtig daran zu erinnern, dass Ströme aus Elektronen in Bewegung bestehen, und Elektronen stoßen sich aufgrund ihrer negativen Ladung natürlicherweise ab. Wenn sich jedoch diese Ladungen in Bewegung befinden, wird diese abstoßende Kraft zu einer anziehenden Kraft, was zu der beobachteten Anziehung zwischen den negativ geladenen Leitern führt.
ID:(11772, 0)
Gegenüberliegende Parallelströme
Notiz
Wenn zwei Ströme in paralleler Richtung, aber in entgegengesetzter Richtung fließen dürfen, beobachten wir eine abstoßende Kraft zwischen den Drähten.
Vergleicht man dieses Experiment mit dem, bei dem der Fluss parallel, aber in gleicher Richtung verläuft, liegt der entscheidende Unterschied in der relativen Geschwindigkeit in letzterem Fall.
ID:(11773, 0)
Drahtinteraktion
Beschreibung
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
(ID 12173)
Beispiele
(ID 1933)
Una alambre por el que circula corriente genera un campo magn tico circular en torno de este.
Por ello con el campo magn tico se calcula mediante:
| $ H_w = \displaystyle\frac{ I }{ 2\pi r }$ |
(ID 12167)
Wenn ein Segment $dl$ eines Drahtes mit einem bestimmten Querschnitt $S$ und einer L nge betrachtet wird, ergibt sich ein Volumen des Drahtes. Durch die Multiplikation dieses Volumens mit der Ladungsdichte $c$ erhalten wir die Anzahl der in ihm enthaltenen Ladungen. Schlie lich, durch die Multiplikation mit der Einheitsladung $q$, erhalten wir die Gesamtladung im Segment.
| $ \Delta Q = q c S dl $ |
(ID 12172)
Der Strom wird durch die folgende Gleichung definiert:
| $ I =\displaystyle\frac{ \Delta Q }{ \Delta t }$ |
und die Ladungen innerhalb eines Drahtsegmentes werden repr sentiert durch:
| $ \Delta Q = q c S dl $ |
Das Verh ltnis der L nge des Segments zur entsprechenden Zeitdauer gibt uns die Geschwindigkeit:
$v =\displaystyle\frac{dl}{dt}$
Daher kann der Strom im Draht wie folgt ausgedr ckt werden:
| $ I = q c S v $ |
(ID 12173)
Wenn ein Draht, durch den ein Strom $I_1$ flie t, ein Magnetfeld erzeugt, das durch folgende Gleichung gegeben ist:
| $ H_w = \displaystyle\frac{ I }{ 2\pi r }$ |
Dieses Feld erzeugt eine magnetische Flussdichte, die durch folgende Gleichung repr sentiert wird:
| $ \vec{B} = \mu_0 \mu_r \vec{H}$ |
Die wiederum eine Kraft pro Segment in einem Draht mit einem Strom $I_2$ erzeugt, definiert als:
| $ d\vec{F} = I d\vec{l} \times \vec{B}$ |
Damit kann die Kraft pro Segment wie folgt ausgedr ckt werden:
| $ \displaystyle\frac{ dF }{ dl } = \mu_0 \mu_r \displaystyle\frac{ I_1 I_2 }{2 \pi r }$ |
(ID 12169)
Wenn zwei Str me in paralleler Weise flie en d rfen, beobachten wir eine anziehende Kraft zwischen den Leitungen.
Es ist wichtig daran zu erinnern, dass Str me aus Elektronen in Bewegung bestehen, und Elektronen sto en sich aufgrund ihrer negativen Ladung nat rlicherweise ab. Wenn sich jedoch diese Ladungen in Bewegung befinden, wird diese absto ende Kraft zu einer anziehenden Kraft, was zu der beobachteten Anziehung zwischen den negativ geladenen Leitern f hrt.
(ID 11772)
Wenn zwei Str me in paralleler Richtung, aber in entgegengesetzter Richtung flie en d rfen, beobachten wir eine absto ende Kraft zwischen den Dr hten.
Vergleicht man dieses Experiment mit dem, bei dem der Fluss parallel, aber in gleicher Richtung verl uft, liegt der entscheidende Unterschied in der relativen Geschwindigkeit in letzterem Fall.
(ID 11773)
ID:(1625, 0)