Usuario:
Resistencia de una inductancia
Definición 
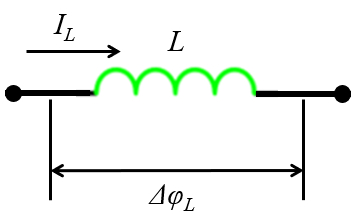
Una inductancia genera según la ley de Lenz un campo que se opone a la corriente que circula por ella lo que se observa como una resistencia. El diagrama para una inductancia conectada a una diferencia de de potencial se muestra a continuación:
ID:(12270, 0)
Resistencia de una capacitancia
Imagen
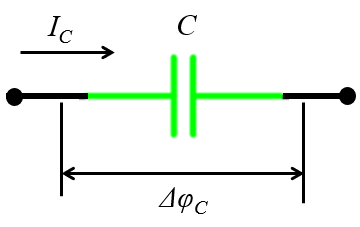
Bajo la corriente alterna una capacitancia es periódicamente polarizada y despolarizada existiendo también una resistencia a dicha situación. En este caso se tiene que la capacitancia conectada se describe con el siguiente diagrama:
ID:(12271, 0)
Resistencia de una inductancia y capacitancia en serie
Nota
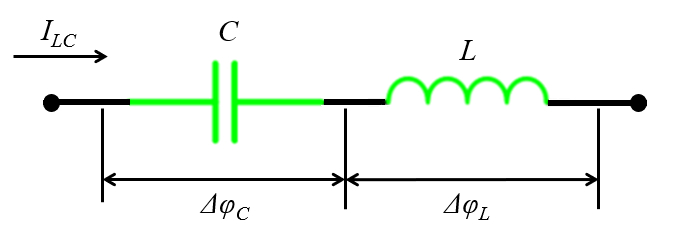
Si se conecta una inductancia y capacitancia en serie con los respectivas caídas de potenciales lo que se muestra en el siguiente diagrama:
ID:(12272, 0)
Resistencia de una inductancia y capacitancia en paralelo
Cita
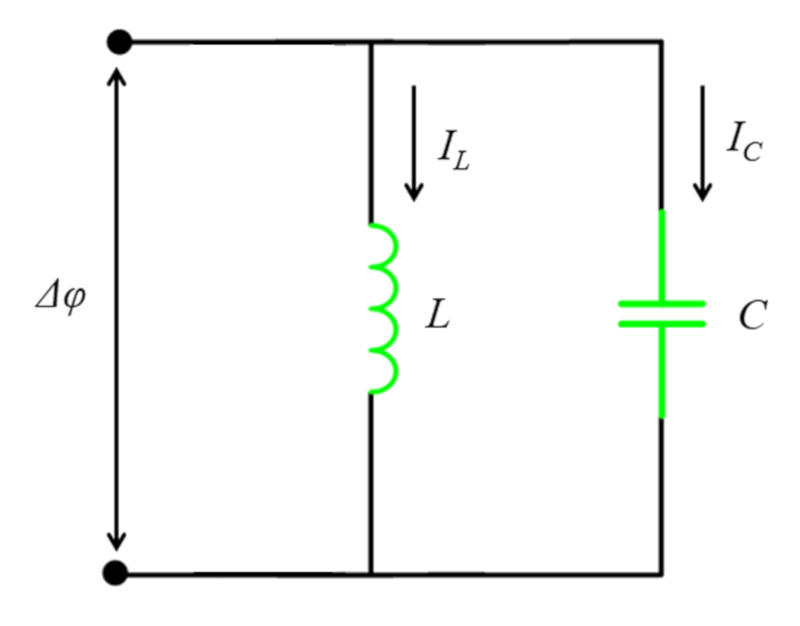
Si se conecta una inductancia y capacitancia en paralelo con los respectivas caídas de potenciales lo que se muestra en el siguiente diagrama:
ID:(12273, 0)
Elementos LC
Storyboard
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
Una inductancia genera seg n la ley de Lenz un campo que se opone a la corriente que circula por ella lo que se observa como una resistencia. El diagrama para una inductancia conectada a una diferencia de de potencial se muestra a continuaci n:
La corriente es proporcional a la diferencia de potencial e inversamente proporcional a la resistencia de la inductancia lo que corresponde un tipo de ley de Ohm para una inductancia.
En particular con
La resistencia de una inductancia depende tanto de la inductividad de el elemento como la frecuencia angular.
En particular con
Bajo la corriente alterna una capacitancia es peri dicamente polarizada y despolarizada existiendo tambi n una resistencia a dicha situaci n. En este caso se tiene que la capacitancia conectada se describe con el siguiente diagrama:
La corriente es proporcional a la diferencia de potencial e inversamente proporcional a la resistencia de la capacitancia lo que corresponde a un tipo de ley de Ohm para una capacitancia.
En particular con
La resistencia de una capacitancia depende tanto de la capacitancia de el elemento como la frecuencia angular.
En particular con
Si se conecta una inductancia y capacitancia en serie con los respectivas ca das de potenciales lo que se muestra en el siguiente diagrama:
La resistencia de una inductancia y una capacitancia en serie depende de las resistencias individuales.
En particular con
La resistencia de una inductancia y una capacitancia en serie es con
Con las resistencias de la inductancia con
y de la capacitancia con
con lo que resulta con
La diferencia de potencial total es con
La relaci n entre potencial y corriente para la suma en serie de LC es con
Si se conecta una inductancia y capacitancia en paralelo con los respectivas ca das de potenciales lo que se muestra en el siguiente diagrama:
La resistencia de una inductancia y una capacitancia en paralelo depende de las resistencias individuales.
En particular con
La resistencia de una inductancia y una capacitancia en serie es con
Con las resistencias de la inductancia con
y de la capacitancia con
con lo que resulta con
La diferencia de potencial total es con
La relaci n entre potencial y corriente para la suma en paralelo de LC es con
ID:(1636, 0)