Examples of electric fields
Storyboard 
Depending on the geometry of the distribution of charges, different electric fields are obtained.
ID:(1564, 0)
Conductor sphere with charge
Definition 
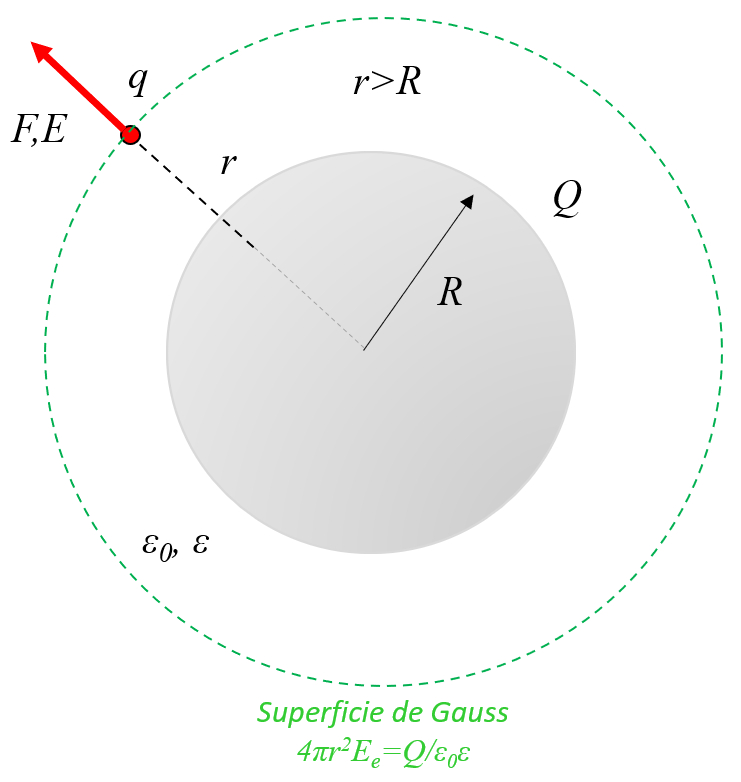
In a conducting sphere with charges, these are distributed on the surface and with it the field inside is null. Outside it behaves like a point charge that is in the center of the sphere:
ID:(11451, 0)
Loaded infinite wire or cylinder, in vacuum
Image 
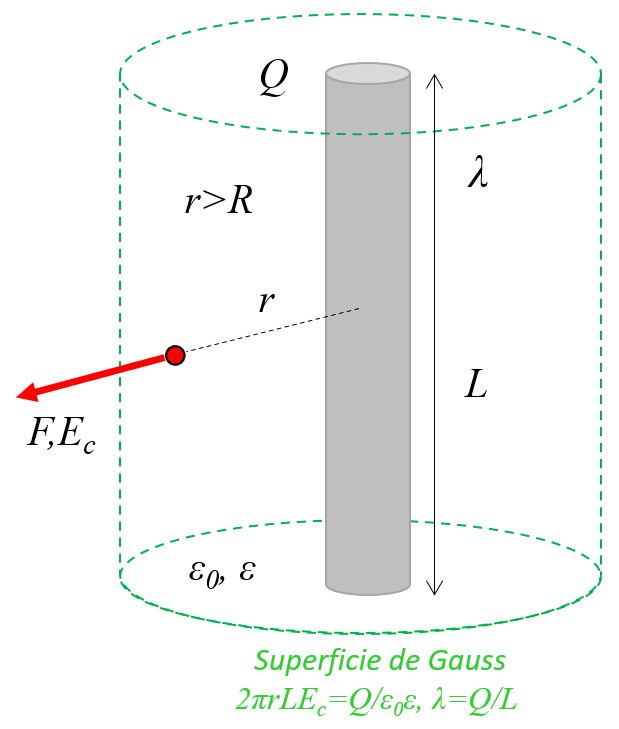
In a conductor wire or cylinder with charges, these are distributed throughout the object, behaving like a long chain of point loads aligned on the axis:
ID:(11452, 0)
Surface of a cylinder
Note 
The surface of a cylinder of radius
ID:(10464, 0)
Insulating sphere with homogeneous charge
Quote 
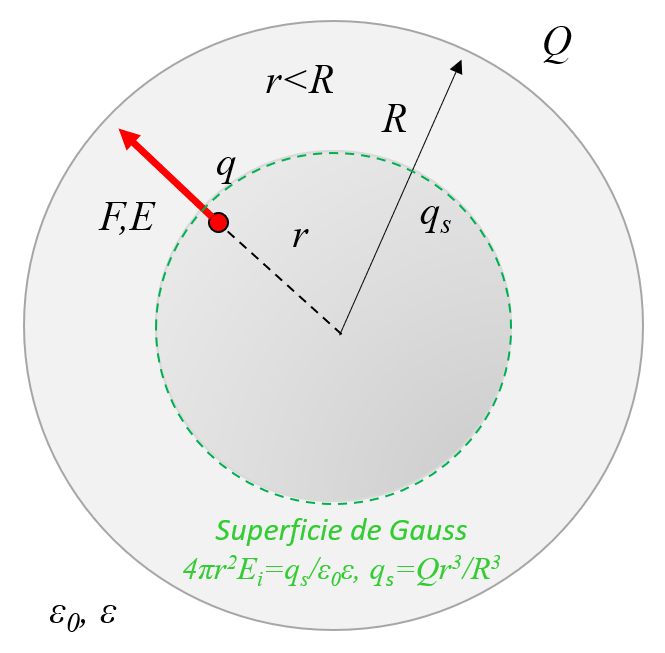
An insulating sphere in which charges have been homogeneously distributed, which cannot be moved because it is an insulating material, has an electric field that grows linearly inside and decreases with the inverse of the radius squared:
ID:(11450, 0)
Infinite conductor plane with load
Exercise 
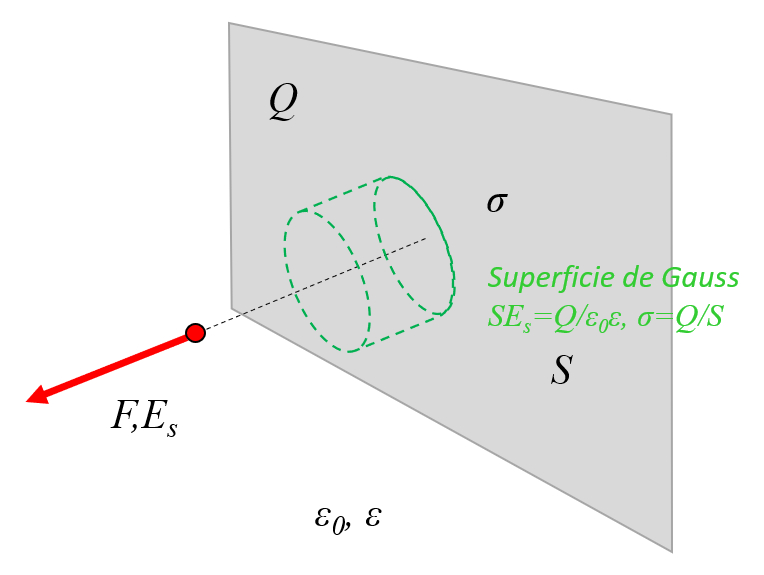
In a conducting plane, a Gaussian surface can be defined as a cylinder. Since the lateral walls are orthogonal to the electric field, they do not contribute to the net flux. Therefore, the only parts that contribute are the cylinder's end caps, which are surfaces parallel to the plane:
ID:(11453, 0)
Two plates with opposite charges
Equation 
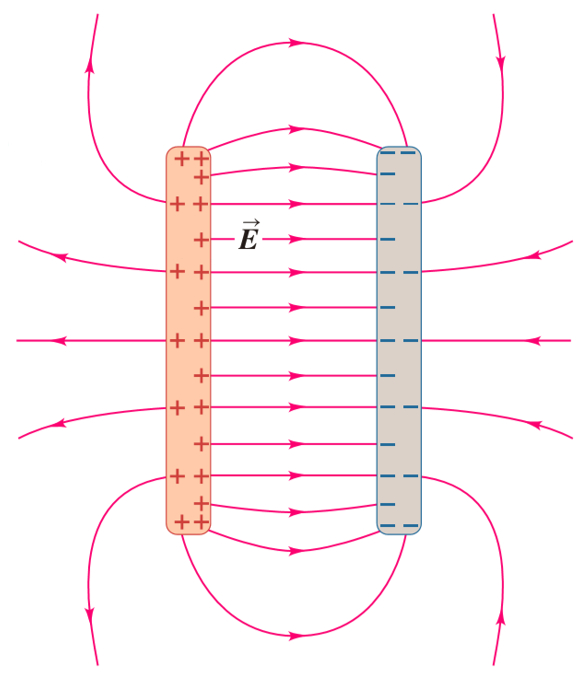
In the case of two plates with opposite charges there is a field of greater intensity between them. However, there is a minor field that can be described with field lines that emerge from one of the plates and return by giving an external turn to the opposite plate:
ID:(11454, 0)
Simple model for two plates with opposite charges
Script 
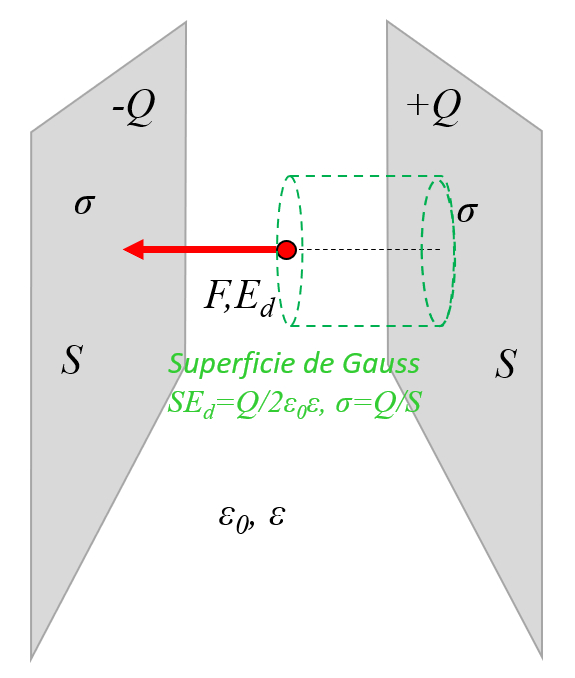
To be able to calculate the field between the two plates in a simple way, it can be assumed that the external field is compensated and that most of it is only between the plates:
ID:(11455, 0)
Examples of electric fields
Storyboard 
Depending on the geometry of the distribution of charges, different electric fields are obtained.
Variables
Calculations
Calculations
Equations
In the case of a spherical Gaussian surface, the electric field ($\vec{E}$) is constant in the direction of the versor normal to the section ($\hat{n}$). Therefore, using the charge ($Q$), the electric field constant ($\epsilon_0$), and the dielectric constant ($\epsilon$), it can be calculated by integrating over the surface where the electric field is constant ($dS$):
with the surface ($S$) for a sphere of radius a distance between charges ($r$):
Thus, the electric field of a point charge ($E_p$) results in:
In the case of a spherical Gaussian surface, the electric field ($\vec{E}$) is constant in the direction of the versor normal to the section ($\hat{n}$). Therefore, using the charge ($Q$), the electric field constant ($\epsilon_0$), and the dielectric constant ($\epsilon$), it can be calculated by integrating over the surface where the electric field is constant ($dS$):
With the surface ($S$) for a cylinder of the axle distance ($r$) and the conductor length ($L$):
and the linear charge density ($\lambda$) calculated with the charge ($Q$):
Thus,
In the case of a cylindrical Gaussian surface, the electric field ($\vec{E}$) is constant in the direction of the versor normal to the section ($\hat{n}$). Therefore, using the variables the charge ($Q$), the electric field constant ($\epsilon_0$), and the dielectric constant ($\epsilon$), the integral over the surface where the electric field is constant ($dS$) can be calculated through the following equation:
For a cylinder characterized by the axle distance ($r$) and the conductor length ($L$), the following applies:
Furthermore, the linear charge density ($\lambda$) is calculated using the charge ($Q$) according to the equation:
Thus, it is established that the electric field, infinite conducting cylinder ($E_c$) is:
In the case of a spherical Gaussian surface, the electric field is constant, so the electric eield ($E$) can be calculated using the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the surface of the conductor ($S$), resulting in:
Given that the surface of a sphere ($S$) is equal to the pi ($\pi$) and the disc radius ($r$), we obtain:
Finally, the electric field, sphere, outer ($E_e$) together with the distance between charges ($r$) is equal to:
Considering a spherical Gaussian surface, the electric field is constant. Therefore, the electric eield ($E$) is equal to the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the surface of the conductor ($S$) as shown by:
Since the surface area of the surface of a sphere ($S$) is equal to the pi ($\pi$) and the disc radius ($r$), we have:
The charge enclosed by the Gaussian surface, with the encapsulated charge on Gauss surface ($q$), the sphere radius ($R$), and the distance between charges ($r$), is given by:
Therefore, the electric field, sphere, interior ($E_i$) results in:
According to Gauss's Law, the variables the surface where the electric field is constant ($dS$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the versor normal to the section ($\hat{n}$), and the electric field ($\vec{E}$) satisfy the following equation:
In the case of a flat Gaussian surface, the field must be constant, so the relationship of the electric eield ($E$) with the surface of the conductor ($S$) is established as:
Since the charge density by area ($\sigma$) is equally defined by:
For the electric field of an infinite plate ($E_s$), the resulting expression is:
In the case of a Gaussian surface for a plane, the electric field ($\vec{E}$) is constant in the direction of the versor normal to the section ($\hat{n}$). Therefore, using the variables the charge ($Q$), the electric field constant ($\epsilon_0$), and the dielectric constant ($\epsilon$), it can be calculated by integrating over the surface where the electric field is constant ($dS$):
Additionally, the charge density by area ($\sigma$) is calculated using the surface ($S$) and the charge ($Q$) according to the following equation:
Therefore, it follows that the electric field, two infinite plates ($E_d$) is:
According to Gauss's Law, the variables the surface where the electric field is constant ($dS$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the versor normal to the section ($\hat{n}$), and the electric field ($\vec{E}$) satisfy the following equation:
the electric eield ($E$) is with and the surface of the conductor ($S$) turns out
Examples
The electric eield ($E$) is with the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the surface of the conductor ($S$) is equal to:
With Gauss's law
for the case that the field is normal and constant on two surface we have
With Gauss's law
for the case that the field is normal and constant on three surface we have
In a conducting sphere with charges, these are distributed on the surface and with it the field inside is null. Outside it behaves like a point charge that is in the center of the sphere:
La superficie de una esfera es con
The electric field of a point charge ($E_p$) is a function of the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the distance between charges ($r$) and is calculated as follows:
Para el caso de una superficie gausseana esf rica el campo es constante por lo que se puede calcular con
con la superficie de una esfera con
A una distancia
In a conductor wire or cylinder with charges, these are distributed throughout the object, behaving like a long chain of point loads aligned on the axis:
The surface of a cylinder of radius
The linear charge density ($\lambda$) is calculated as the charge ($Q$) divided by the conductor length ($L$):
The electric field of an infinite wire ($E_w$) is a function of the linear charge density ($\lambda$), the axle distance ($r$), the dielectric constant ($\epsilon$) and the electric field constant ($\epsilon_0$) and is calculated through:
The electric field, infinite conducting cylinder ($E_c$) is with the pi ($\pi$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the linear charge density ($\lambda$) and the axle distance ($r$) is equal to:
An insulating sphere in which charges have been homogeneously distributed, which cannot be moved because it is an insulating material, has an electric field that grows linearly inside and decreases with the inverse of the radius squared:
The electric field, sphere, outer ($E_e$) is with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the distance between charges ($r$) is equal to:
In the case of a the sphere radius ($R$) sphere with homogeneous charge, the Gaussian surface for the distance between charges ($r$) includes the encapsulated charge on Gauss surface ($q$) for the charge ($Q$) :
The electric field, sphere, interior ($E_i$) is with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the sphere radius ($R$) and the distance between charges ($r$) is equal to:
In a conducting plane, a Gaussian surface can be defined as a cylinder. Since the lateral walls are orthogonal to the electric field, they do not contribute to the net flux. Therefore, the only parts that contribute are the cylinder's end caps, which are surfaces parallel to the plane:
The surface charge density is calculated by dividing the total charge by the surface area. Therefore, the relationship between the charge density by area ($\sigma$) and the charge ($Q$) with the surface of the conductor ($S$) is established as:
The electric field of an infinite plate ($E_s$) is with the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the charge density by area ($\sigma$) equal to:
In the case of two plates with opposite charges there is a field of greater intensity between them. However, there is a minor field that can be described with field lines that emerge from one of the plates and return by giving an external turn to the opposite plate:
To be able to calculate the field between the two plates in a simple way, it can be assumed that the external field is compensated and that most of it is only between the plates:
The electric field, two infinite plates ($E_d$) is with the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the charge density by area ($\sigma$) is equal to:
ID:(1564, 0)
