Ejemplos de campos eléctricos
Storyboard 
Según la geometría de la distribución de cargas se obtienen distintos campos eléctricos.
ID:(1564, 0)
Esfera conductora con carga
Definición 
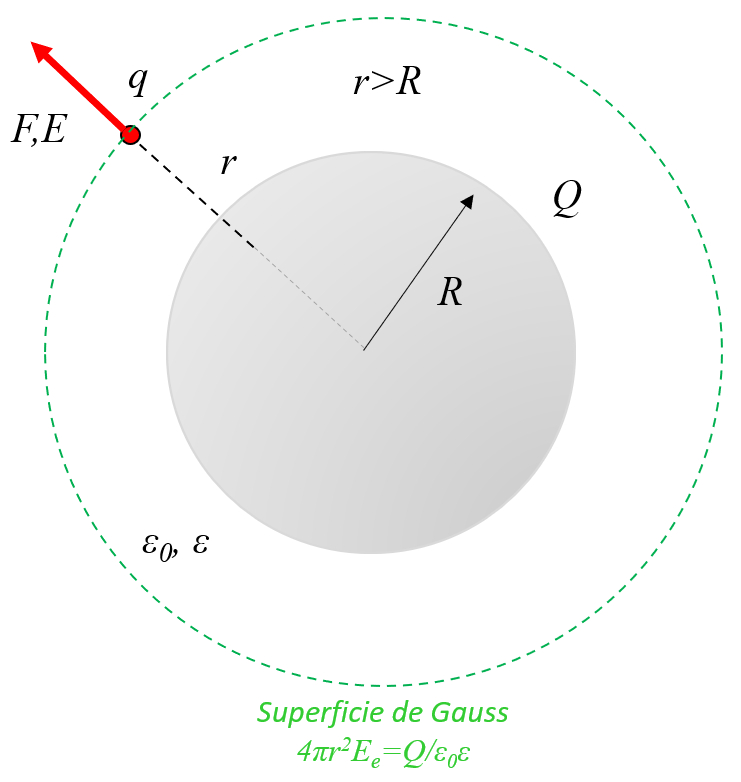
En una esfera conductor con cargas, estas se distribuyen en la superficie y con ello el campo en su interior es nulo. En el exterior se comporta como una carga puntual que esta en el centro de la esfera:
ID:(11451, 0)
Alambre o cilindro infinito con carga, en el vacío
Imagen 
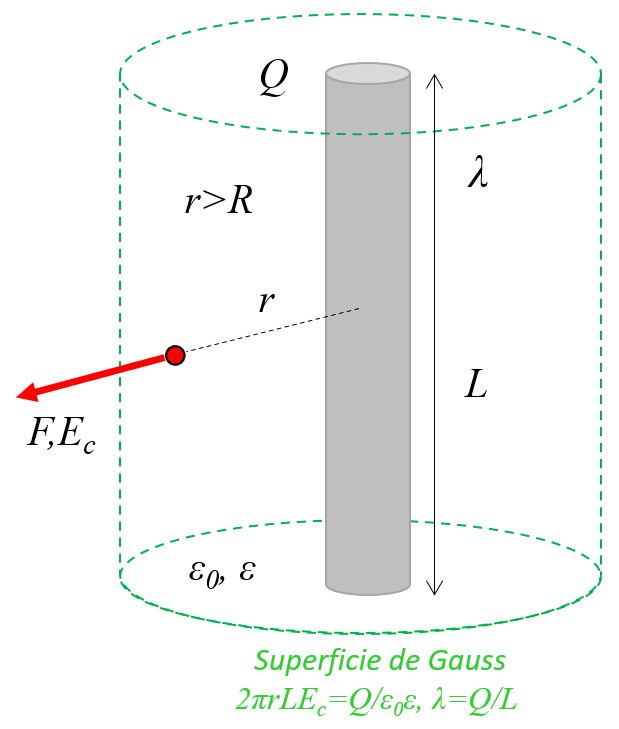
En una alambre o cilindro conductor con cargas, estas se distribuyen a lo largo del objeto comportándose como una larga cadena de cargas puntuales alineadas en el eje:
ID:(11452, 0)
Superficie de un cilindro
Nota 
La superficie de un cilindro de radio
ID:(10464, 0)
Esfera aislante con carga homogénea
Cita 
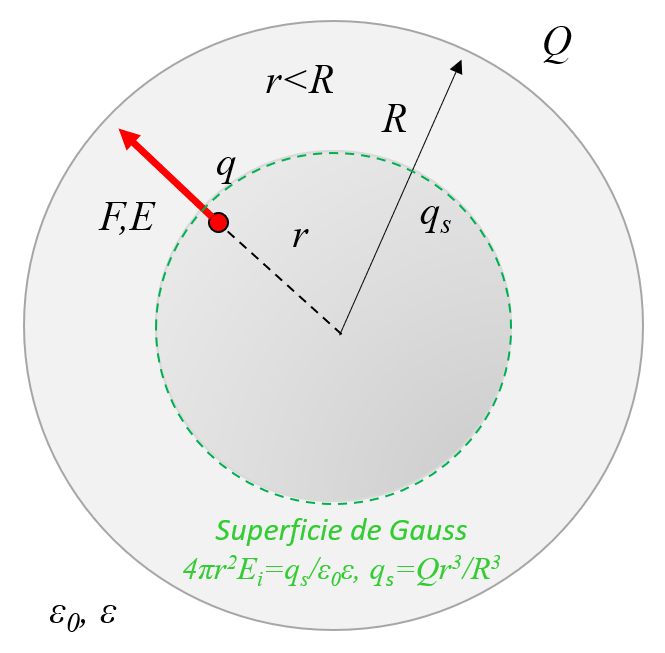
Una esfera aislante en que se ha distribuido homogéneamente cargas, que no se pueden mover por ser un material aislante, tiene un campo eléctrico que crece linealmente en el interior y decrece con el inverso del radio al cuadrado:
ID:(11450, 0)
Plano conductor infinito con carga
Ejercicio 
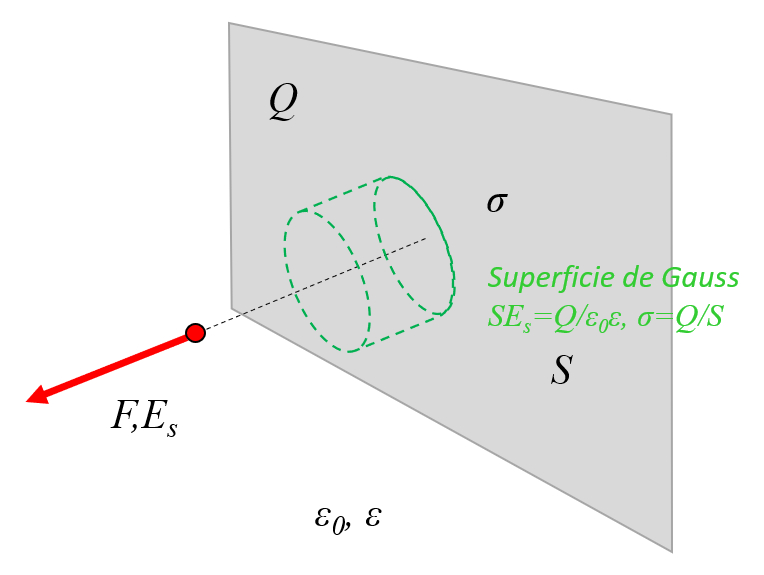
En un plano conductor, es posible definir una superficie gaussiana en forma de cilindro. Dado que las paredes laterales son ortogonales al campo eléctrico, no contribuyen al flujo neto. Por lo tanto, las únicas partes que contribuyen son las tapas del cilindro, que son superficies paralelas al plano:
ID:(11453, 0)
Dos placas con cargas opuestas
Ecuación 
En el caso de dos placas con cargas opuestas existe un campo de mayor intensidad entre estas. Sin embargo existe un campo menor que se puede describir con lineas de campo que surjan de una de las placas y vuelven dando una vuelta externa a la placa opuesta:
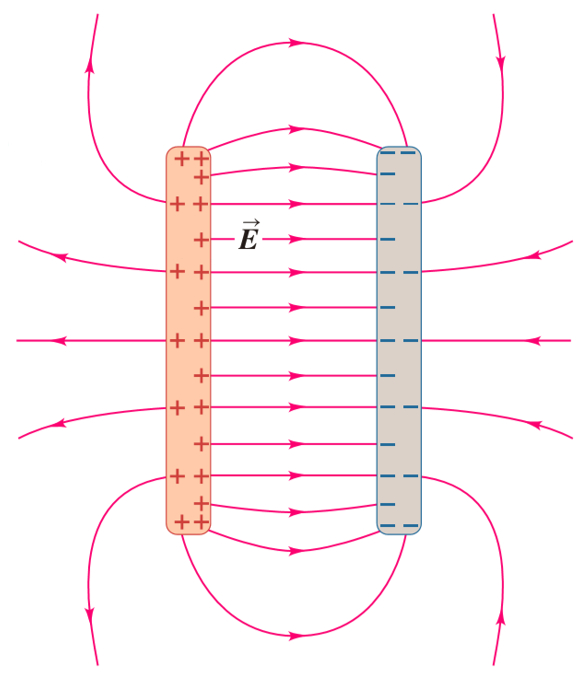
ID:(11454, 0)
Modelo simple para dos placas con cargas opuestas
Script 
Para poder calcular en forma simple el campo entre las dos placas se puede asumir que el campo externo se compensa y que la mayor parte es solo entre las placas:
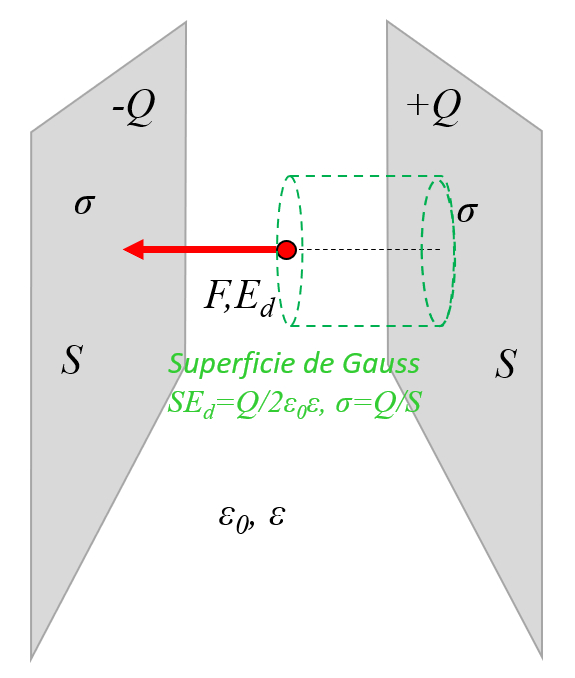
ID:(11455, 0)
Ejemplos de campos eléctricos
Descripción 
Según la geometría de la distribución de cargas se obtienen distintos campos eléctricos.
Variables
Cálculos
Cálculos
Ecuaciones
None
(ID 4731)
En el caso de una superficie gaussiana esf rica, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
con la superficie ($S$) para una esfera de radio una distancia entre cargas ($r$):
| $ S = 4 \pi r ^2$ |
De esta manera, el campo eléctrico de una carga puntual ($E_p$) resulta en:
| $ E_p =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}$ |
(ID 11442)
En el caso de una superficie gaussiana esf rica, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Con la superficie ($S$) para un cilindro de la distancia al eje ($r$) y el largo del conductor ($L$):
| $ S =2 \pi r h $ |
y la densidad lineal de carga ($\lambda$) que se calcula con la carga ($Q$)
| $ \lambda = \displaystyle\frac{ Q }{ L }$ |
Por ello se tiene que el campo eléctrico de un alambre infinito ($E_w$) es:
| $ E_w =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }$ |
(ID 11444)
En el caso de una superficie gaussiana cil ndrica, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando las variables la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular la integral sobre la superficie en que campo eléctrico es constante ($dS$) mediante la siguiente ecuaci n:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Para un cilindro caracterizado por la distancia al eje ($r$) y el largo del conductor ($L$), se aplica:
| $ S =2 \pi r h $ |
Adem s, la densidad lineal de carga ($\lambda$) se calcula utilizando la carga ($Q$) seg n la ecuaci n:
| $ \lambda = \displaystyle\frac{ Q }{ L }$ |
As , se establece que el campo eléctrico, cilindro conductor infinito ($E_c$) es:
| $ E_c =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }$ |
(ID 11445)
Para el caso de una superficie gausseana esf rica el campo es constante por lo que se puede calcular el campo eléctrico ($E$) con la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la área del conductor ($S$) siendo igual a:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Como la superficie de una esfera ($S$) es con el pi ($\pi$) y el radio de un disco ($r$) igual a:
| $ S = 4 \pi r ^2$ |
el campo eléctrico, esfera, exterior ($E_e$) es con la distancia entre cargas ($r$) igual
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
(ID 11446)
Para el caso de una superficie gaussiana esf rica, el campo es constante y, por lo tanto, el campo eléctrico ($E$) es igual a la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la área del conductor ($S$) seg n:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Dado que la superficie de la superficie de una esfera ($S$) es igual a el pi ($\pi$) y el radio de un disco ($r$), se tiene:
| $ S = 4 \pi r ^2$ |
La carga encerrada en la superficie gaussiana, con la carga encapsulada en la superficie de Gauss ($q$), el radio de la esfera ($R$) y la distancia entre cargas ($r$), es:
| $ q =\displaystyle\frac{ r ^3}{ R ^3} Q $ |
Por lo tanto, el campo eléctrico, esfera, interior ($E_i$) resulta en:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
(ID 11447)
Seg n la ley de Gauss, las variables la superficie en que campo eléctrico es constante ($dS$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), el versor normal a la sección ($\hat{n}$) y el campo eléctrico ($\vec{E}$) cumplen con la siguiente ecuaci n:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
En el caso de una superficie gaussiana plana, el campo debe ser constante, por lo que la relaci n de el campo eléctrico ($E$) con la área del conductor ($S$) se establece como:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Dado que la densidad de carga por área ($\sigma$) se define igualmente por:
| $ \sigma = \displaystyle\frac{ Q }{ S }$ |
Para el campo eléctrico de una placa infinita ($E_s$), la expresi n resultante es:
| $ E_s =\displaystyle\frac{ \sigma }{ 2 \epsilon_0 \epsilon }$ |
(ID 11448)
En el caso de una superficie gaussiana plana, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando las variables la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Adem s, la densidad de carga por área ($\sigma$) se calcula utilizando la superficie ($S$) y la carga ($Q$) seg n la siguiente ecuaci n:
| $ \sigma = \displaystyle\frac{ Q }{ S }$ |
Por lo tanto, se concluye que el campo eléctrico, dos placas infinitas ($E_d$) es:
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
(ID 11449)
Seg n la ley de Gauss, las variables la superficie en que campo eléctrico es constante ($dS$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), el versor normal a la sección ($\hat{n}$) y el campo eléctrico ($\vec{E}$) cumplen con la siguiente ecuaci n:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
el campo eléctrico ($E$) es con y la área del conductor ($S$) resulta
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
(ID 11456)
Ejemplos
El campo eléctrico ($E$) es con la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la área del conductor ($S$) es igual a:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
(ID 11456)
Con la ley de Gauss
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
para el caso de que el campo es normal y constante sobre dos superficie se tiene
| $ E_1 S_1 + E_2 S_2 = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$ |
(ID 11458)
Con la ley de Gauss
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
para el caso de que el campo es normal y constante sobre tres superficie se tiene
| $ E_1 S_1 + E_2 S_2 + E_3 S_3 = \displaystyle\frac{ Q }{ \epsilon\epsilon_0 }$ |
(ID 11457)
En una esfera conductor con cargas, estas se distribuyen en la superficie y con ello el campo en su interior es nulo. En el exterior se comporta como una carga puntual que esta en el centro de la esfera:

(ID 11451)
La superficie de una esfera es con igual a
| $ S = 4 \pi r ^2$ |
(ID 4731)
El campo eléctrico de una carga puntual ($E_p$) es una funci n de la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) y se calcula mediante:
| $ E_p =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}$ |
(ID 11442)
Para el caso de una superficie gausseana esf rica el campo es constante por lo que se puede calcular con área del conductor $m^2$, campo eléctrico $V/m$, carga $C$ y constante dieléctrica $-$ mediante
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
con la superficie de una esfera con radio de un disco $m$ y superficie de una esfera $m^2$
| $ S = 4 \pi r ^2$ |
A una distancia
| $ E_f =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}\theta( r - R )$ |
La funci n
(ID 11443)
En una alambre o cilindro conductor con cargas, estas se distribuyen a lo largo del objeto comport ndose como una larga cadena de cargas puntuales alineadas en el eje:

(ID 11452)
La superficie de un cilindro de radio
(ID 10464)
La densidad lineal de carga ($\lambda$) se calcula como la carga ($Q$) dividida el largo del conductor ($L$):
| $ \lambda = \displaystyle\frac{ Q }{ L }$ |
(ID 11459)
El campo eléctrico de un alambre infinito ($E_w$) es una funci n de la densidad lineal de carga ($\lambda$), la distancia al eje ($r$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$) y se calcula mediante:
| $ E_w =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }$ |
(ID 11444)
El campo eléctrico, cilindro conductor infinito ($E_c$) es con el pi ($\pi$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), la densidad lineal de carga ($\lambda$) y la distancia al eje ($r$) es igual a:
| $ E_c =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }$ |
(ID 11445)
Una esfera aislante en que se ha distribuido homog neamente cargas, que no se pueden mover por ser un material aislante, tiene un campo el ctrico que crece linealmente en el interior y decrece con el inverso del radio al cuadrado:

(ID 11450)
El campo eléctrico, esfera, exterior ($E_e$) es con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) es igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
(ID 11446)
En el caso de una esfera de el radio de la esfera ($R$) con carga homog nea, la superficie de Gauss para la distancia entre cargas ($r$) incluye la carga encapsulada en la superficie de Gauss ($q$) para la carga ($Q$):
| $ q =\displaystyle\frac{ r ^3}{ R ^3} Q $ |
(ID 11461)
El campo eléctrico, esfera, interior ($E_i$) es con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), el radio de la esfera ($R$) y la distancia entre cargas ($r$) es igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
(ID 11447)
En un plano conductor, es posible definir una superficie gaussiana en forma de cilindro. Dado que las paredes laterales son ortogonales al campo el ctrico, no contribuyen al flujo neto. Por lo tanto, las nicas partes que contribuyen son las tapas del cilindro, que son superficies paralelas al plano:

(ID 11453)
La densidad superficial de carga se calcula dividiendo la carga total por el rea de la superficie. Por lo tanto, la relaci n entre la densidad de carga por área ($\sigma$) y la carga ($Q$) con la área del conductor ($S$) se establece como:
| $ \sigma = \displaystyle\frac{ Q }{ S }$ |
(ID 11460)
El campo eléctrico de una placa infinita ($E_s$) es con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) igual a:
| $ E_s =\displaystyle\frac{ \sigma }{ 2 \epsilon_0 \epsilon }$ |
(ID 11448)
En el caso de dos placas con cargas opuestas existe un campo de mayor intensidad entre estas. Sin embargo existe un campo menor que se puede describir con lineas de campo que surjan de una de las placas y vuelven dando una vuelta externa a la placa opuesta:

(ID 11454)
Para poder calcular en forma simple el campo entre las dos placas se puede asumir que el campo externo se compensa y que la mayor parte es solo entre las placas:

(ID 11455)
El campo eléctrico, dos placas infinitas ($E_d$) es con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) es igual a:
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
(ID 11449)
ID:(1564, 0)
