Utilizador:
Lei de Coulomb
Storyboard 
Cargas exercem forças entre si; se são do mesmo sinal, a força é repulsiva, e se são de sinais opostos, é atrativa. Essa força é regida pela lei de Coulomb e é proporcional ao produto das magnitudes das cargas e inversamente proporcional ao quadrado da distância entre elas. A direção da força é ao longo da linha que conecta as duas cargas.
ID:(1497, 0)
Descrição fenomenológica da interação entre cargas
Imagem
Uma maneira de entender a natureza da força entre duas cargas é considerar que a interação é modelada através da troca de partículas, que neste caso são fótons. O número desses mensageiros é proporcional à carga que os emite e também à probabilidade de serem capturados pela outra carga. Nesse sentido,
a força deveria ser proporcional ao produto de ambas as cargas.
Por outro lado, esses mensageiros são emitidos em todas as direções, distribuindo-se sobre uma esfera imaginária ao redor da carga. A área superficial desta esfera é $4\pi r^2$, onde
r é o raio, correspondente à distância entre as cargas. Portanto,
a força deveria ser inversamente proporcional ao quadrado da distância entre as cargas, ou seja, inversamente proporcional à área superficial da esfera centrada na outra carga.
Essa distribuição pode ser visualmente representada como a superfície ao redor de uma carga e o 'cone' dentro do qual os fótons são capturados pela outra carga.
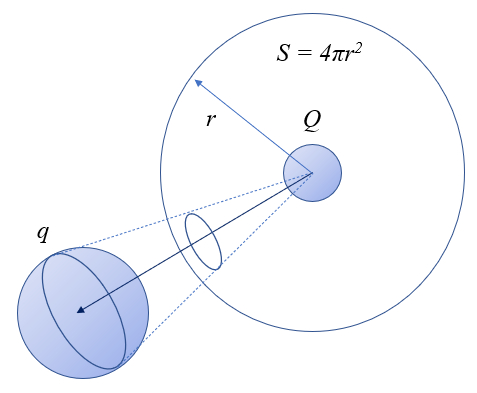
Assim, a força, como uma quantidade escalar, teria a forma
$F \propto \displaystyle\frac{qQ}{4\pi r^2}$
ID:(11363, 0)
Força de Coulomb
Nota
A força entre cargas elétricas depende de:
• As magnitudes das cargas, sendo positiva se ambas as cargas tiverem o mesmo sinal e negativa se forem de sinais opostos.
• A magnitude da força diminui com o quadrado da distância entre as cargas.
• A direção da força se alinha ao longo da linha que conecta ambas as cargas.
Por essa razão, Coulomb [1] formulou que la força com massa constante ($F$) é proporcional ao produto das magnitudes das cargas la carga de teste ($q$) e la charge ($Q$), inversamente proporcional ao quadrado de la distância ($r$) que as separa, com constantes de proporcionalidade la constante dielétrica ($\epsilon$) e la constante de campo elétrico ($\epsilon_0$):
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
A força de Coulomb atua na direção de la distância ($r$), que pode ser representada por o verson ($\hat{r}$). Portanto, a equação anterior pode ser generalizada como:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
[1] "Premier Mémoire sur lÉlectricité et le Magnétisme" (Primeiro Memória sobre Eletricidade e Magnetismo), Charles-Augustin de Coulomb, Académie Royale des Sciences em Paris, 1785.
ID:(1697, 0)
Lei de Coulomb para uma distribuição de carga
Citar
La força ($\vec{F}$), gerada entre duas cargas representadas por la carga de teste ($q$) e la charge ($Q$), que estão a uma distância de la distância ($r$), é calculada usando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$). A direção é ao longo de la distância ($r$), o que pode ser representado por o verson ($\hat{r}$). Portanto, a lei é expressa como:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
Se considerarmos que la distância ($r$) é a distância entre la posição 1 ($\vec{s}_1$) e la posição 2 ($\vec{s}_2$), isso pode ser expresso como:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
e para o verson ($\hat{r}$), usando:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
Associando la posição ($\vec{r}$) com la posição 2 ($\vec{s}_2$), la posição 1 ($\vec{s}_1$) com la posição de uma carga i ($\vec{u}_i$) e la charge ($Q$) com la carga iônica i ($Q_i$), pode-se concluir que o total de la força ($\vec{F}$) é:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
ID:(15773, 0)
Lei de Coulomb
Storyboard
Cargas exercem forças entre si; se são do mesmo sinal, a força é repulsiva, e se são de sinais opostos, é atrativa. Essa força é regida pela lei de Coulomb e é proporcional ao produto das magnitudes das cargas e inversamente proporcional ao quadrado da distância entre elas. A direção da força é ao longo da linha que conecta as duas cargas.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
La força ($\vec{F}$), gerada entre duas cargas representadas por la carga de teste ($q$) e la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada usando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$). A dire o ao longo de la distância ($r$), o que pode ser representado por o verson ($\hat{r}$). Portanto, a lei expressa como:
Se considerarmos que la distância ($r$) a dist ncia entre la posição 1 ($\vec{s}_1$) e la posição 2 ($\vec{s}_2$), isso pode ser expresso como:
e para o verson ($\hat{r}$), usando:
Associando la posição ($\vec{r}$) com la posição 2 ($\vec{s}_2$), la posição 1 ($\vec{s}_1$) com la posição de uma carga i ($\vec{u}_i$) e la charge ($Q$) com la carga iônica i ($Q_i$), pode-se concluir que o total de la força ($\vec{F}$) :
A magnitude de la força com massa constante ($F$) gerada entre duas cargas, representadas por la carga de teste ($q$) e la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada usando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte maneira:
Para modelar la força ($\vec{F}$) entre as cargas na forma vetorial, deve-se incluir a dire o em que ela atua, definida por o verson ($\hat{r}$), resultando em:
Exemplos
Uma maneira de entender a natureza da for a entre duas cargas considerar que a intera o modelada atrav s da troca de part culas, que neste caso s o f tons. O n mero desses mensageiros proporcional carga que os emite e tamb m probabilidade de serem capturados pela outra carga. Nesse sentido,
a for a deveria ser proporcional ao produto de ambas as cargas.
Por outro lado, esses mensageiros s o emitidos em todas as dire es, distribuindo-se sobre uma esfera imagin ria ao redor da carga. A rea superficial desta esfera $4\pi r^2$, onde
r o raio, correspondente dist ncia entre as cargas. Portanto,
a for a deveria ser inversamente proporcional ao quadrado da dist ncia entre as cargas, ou seja, inversamente proporcional rea superficial da esfera centrada na outra carga.
Essa distribui o pode ser visualmente representada como a superf cie ao redor de uma carga e o 'cone' dentro do qual os f tons s o capturados pela outra carga.
Assim, a for a, como uma quantidade escalar, teria a forma
$F \propto \displaystyle\frac{qQ}{4\pi r^2}$
A for a entre cargas el tricas depende de:
• As magnitudes das cargas, sendo positiva se ambas as cargas tiverem o mesmo sinal e negativa se forem de sinais opostos.
• A magnitude da for a diminui com o quadrado da dist ncia entre as cargas.
• A dire o da for a se alinha ao longo da linha que conecta ambas as cargas.
Por essa raz o, Coulomb [1] formulou que la força com massa constante ($F$) proporcional ao produto das magnitudes das cargas la carga de teste ($q$) e la charge ($Q$), inversamente proporcional ao quadrado de la distância ($r$) que as separa, com constantes de proporcionalidade la constante dielétrica ($\epsilon$) e la constante de campo elétrico ($\epsilon_0$):
A for a de Coulomb atua na dire o de la distância ($r$), que pode ser representada por o verson ($\hat{r}$). Portanto, a equa o anterior pode ser generalizada como:
[1] "Premier M moire sur l lectricit et le Magn tisme" (Primeiro Mem ria sobre Eletricidade e Magnetismo), Charles-Augustin de Coulomb, Acad mie Royale des Sciences em Paris, 1785.
La força ($\vec{F}$), gerada entre duas cargas representadas por la carga de teste ($q$) e la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada usando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$). A dire o ao longo de la distância ($r$), o que pode ser representado por o verson ($\hat{r}$). Portanto, a lei expressa como:
Se considerarmos que la distância ($r$) a dist ncia entre la posição 1 ($\vec{s}_1$) e la posição 2 ($\vec{s}_2$), isso pode ser expresso como:
e para o verson ($\hat{r}$), usando:
Associando la posição ($\vec{r}$) com la posição 2 ($\vec{s}_2$), la posição 1 ($\vec{s}_1$) com la posição de uma carga i ($\vec{u}_i$) e la charge ($Q$) com la carga iônica i ($Q_i$), pode-se concluir que o total de la força ($\vec{F}$) :
A magnitude de la força com massa constante ($F$) gerada entre duas cargas, representadas por la carga de teste ($q$) e la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada usando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte maneira:
La força ($\vec{F}$), gerada entre duas cargas representadas por la carga de teste ($q$) e la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada usando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$). A dire o ao longo de la distância ($r$), que pode ser representada por o verson ($\hat{r}$). Portanto, a lei escrita como:
La força ($\vec{F}$) sobre la carga de teste ($q$) em la posição ($\vec{r}$) depender de o número de cobranças ($N$), contabilizadas com o ndice $i$ representadas por la carga iônica i ($Q_i$) localizadas em la posição de uma carga i ($\vec{u}_i$). Com os par metros la constante dielétrica ($\epsilon$) e la constante de campo elétrico ($\epsilon_0$), isso pode ser escrito como:
ID:(1497, 0)