Benützer:
Coulombsches Gesetz
Storyboard 
Ladungen üben Kräfte aufeinander aus; sind sie gleichnamig, ist die Kraft abstoßend, und bei ungleichnamigen Ladungen ist sie anziehend. Diese Kraft wird durch das Coulombsche Gesetz beschrieben und ist proportional zum Produkt der Beträge der Ladungen und umgekehrt proportional zum Quadrat des Abstands zwischen ihnen. Die Richtung der Kraft verläuft entlang der Verbindungslinie der beiden Ladungen.
ID:(1497, 0)
Phänomenologische Beschreibung der Wechselwirkung zwischen Ladungen
Konzept
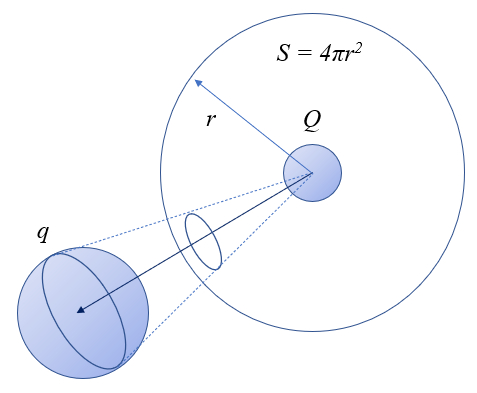
Eine Möglichkeit, die Natur der Kraft zwischen zwei Ladungen zu verstehen, besteht darin, die Interaktion als Austausch von Teilchen zu modellieren, die in diesem Fall Photonen sind. Die Anzahl dieser Botenteilchen ist proportional zur Ladung, die sie aussendet, sowie zur Wahrscheinlichkeit, dass sie von der anderen Ladung eingefangen werden. In diesem Sinne,
sollte die Kraft proportional zum Produkt beider Ladungen sein.
Andererseits werden diese Boten in alle Richtungen ausgesendet und verteilen sich über eine imaginäre Kugel, die die Ladung umgibt. Die Oberfläche dieser Kugel beträgt $4\pi r^2$, wobei
r der Radius ist, der dem Abstand zwischen den Ladungen entspricht. Daher,
sollte die Kraft umgekehrt proportional zum Quadrat des Abstands zwischen den Ladungen sein, das heißt, umgekehrt proportional zur Oberfläche der Kugel, die um die andere Ladung zentriert ist.
Diese Verteilung kann grafisch als die Oberfläche um eine Ladung und der 'Kegel', in dem die Photonen von der anderen Ladung eingefangen werden, dargestellt werden.
Somit hätte die Kraft als skalare Größe die Form
$F \propto \displaystyle\frac{qQ}{4\pi r^2}$
ID:(11363, 0)
Coulombkraft
Konzept
Die Kraft zwischen elektrischen Ladungen hängt ab von:
• Den Größen der Ladungen, wobei die Kraft positiv ist, wenn beide Ladungen das gleiche Vorzeichen haben, und negativ, wenn sie entgegengesetzte Vorzeichen haben.
• Die Stärke der Kraft nimmt mit dem Quadrat des Abstands zwischen den Ladungen ab.
• Die Richtung der Kraft verläuft entlang der Linie, die beide Ladungen verbindet.
Aus diesem Grund formulierte Coulomb [1], dass die Kraft mit konstanter Masse ($F$) proportional zum Produkt der Ladungsmengen die Test Ladung ($q$) und die Ladung ($Q$) ist, und umgekehrt proportional zum Quadrat von die Entfernung ($r$), dem Abstand, der sie trennt, mit den Proportionalitätskonstanten die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$):
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
Die Coulomb-Kraft wirkt in der Richtung von die Entfernung ($r$), die durch der Verson ($\hat{r}$) dargestellt werden kann. Daher kann die vorherige Gleichung wie folgt verallgemeinert werden:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
[1] "Premier Mémoire sur lÉlectricité et le Magnétisme" (Erstes Memoire über Elektrizität und Magnetismus), Charles-Augustin de Coulomb, Académie Royale des Sciences in Paris, 1785.
ID:(1697, 0)
Coulombsches Gesetz für eine Ladungsverteilung
Konzept
Die Kraft ($\vec{F}$), die zwischen zwei Ladungen erzeugt wird, dargestellt durch die Test Ladung ($q$) und die Ladung ($Q$), die sich in einem Abstand von die Entfernung ($r$) befinden, wird mithilfe von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) berechnet. Die Richtung verläuft entlang von die Entfernung ($r$), was durch der Verson ($\hat{r}$) dargestellt werden kann. Daher wird das Gesetz wie folgt ausgedrückt:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
Wenn die Entfernung ($r$) als der Abstand zwischen die Position 1 ($\vec{s}_1$) und die Position 2 ($\vec{s}_2$) betrachtet wird, kann dies wie folgt ausgedrückt werden:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
und für der Verson ($\hat{r}$) gilt:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
Indem die Position ($\vec{r}$) mit die Position 2 ($\vec{s}_2$), die Position 1 ($\vec{s}_1$) mit die Position einer Ladung i ($\vec{u}_i$) und die Ladung ($Q$) mit die Ladung der Ionen i ($Q_i$) assoziiert werden, kann man schließen, dass die gesamte die Kraft ($\vec{F}$) ist:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
ID:(15773, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $
&F = q * Q * &&r /(4* pi * e_0 * e * r ^2)
$ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$
F = q * Q /(4* pi * e_0 * e * r ^2)
$ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$
F =@SUM( q * Q_i *( &r - &u_i )/ | &r - &u_i |^3, i , N )/(4* pi * epsilon_0 * epsilon )
$ r =| \vec{s}_2 - \vec{s}_1 |$
r = @MOD( &s_2 - &s_1 )
$ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$
r =( x_2 - x_1 )/abs( x_2 - x_1 )
ID:(15323, 0)
Entfernung
Gleichung
Die Entfernung ($r$) stellt den Abstand zwischen die Position 1 ($\vec{s}_1$) und die Position 2 ($\vec{s}_2$) dar, der wie folgt ausgedrückt werden kann:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
ID:(10390, 0)
Versor des Coulombschen Gesetzes
Gleichung
Der Verson ($\hat{r}$) entlang der Entfernung zwischen die Position 1 ($\vec{s}_1$) und die Position 2 ($\vec{s}_2$) kann mithilfe der folgenden Formel berechnet werden:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
ID:(10391, 0)
Coulomb-Gesetz
Gleichung
Die Größe von die Kraft mit konstanter Masse ($F$), die zwischen zwei Ladungen, dargestellt durch die Test Ladung ($q$) und die Ladung ($Q$), die sich in einem Abstand von die Entfernung ($r$) befinden, erzeugt wird, wird mithilfe von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) wie folgt berechnet:
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
None
ID:(3212, 0)
Coulombsches Gesetz in Vektorform
Gleichung
Die Kraft ($\vec{F}$), die zwischen zwei Ladungen erzeugt wird, dargestellt durch die Test Ladung ($q$) und die Ladung ($Q$), die sich in einem Abstand von die Entfernung ($r$) befinden, wird mithilfe von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) berechnet. Die Richtung verläuft entlang die Entfernung ($r$), was durch der Verson ($\hat{r}$) dargestellt werden kann. Daher wird das Gesetz wie folgt geschrieben:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
Die Größe von die Kraft mit konstanter Masse ($F$), die zwischen zwei Ladungen erzeugt wird, dargestellt durch die Test Ladung ($q$) und die Ladung ($Q$), die sich in einem Abstand von die Entfernung ($r$) befinden, wird mithilfe von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) wie folgt berechnet:
| $ F =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2}$ |
Um die Kraft ($\vec{F}$) zwischen Ladungen in Vektorform zu modellieren, muss die Richtung, in der sie wirkt, einbezogen werden, definiert durch der Verson ($\hat{r}$), was zu folgendem führt:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
ID:(15772, 0)
Coulombsches Gesetz für eine Ladungsverteilung
Gleichung
Die Kraft ($\vec{F}$) auf die Test Ladung ($q$) bei die Position ($\vec{r}$) hängt von der Anzahl der Ladunegn ($N$) ab, die mit dem Index $i$ erfasst und durch die Ladung der Ionen i ($Q_i$) dargestellt werden, das sich bei die Position einer Ladung i ($\vec{u}_i$) befindet. Mit den Parametern die Dielektrizitätskonstante ($\epsilon$) und die Elektrische Feldkonstante ($\epsilon_0$) kann dies wie folgt geschrieben werden:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
Die Kraft ($\vec{F}$), die zwischen zwei Ladungen erzeugt wird, dargestellt durch die Test Ladung ($q$) und die Ladung ($Q$), die sich in einem Abstand von die Entfernung ($r$) befinden, wird mithilfe von die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) berechnet. Die Richtung verläuft entlang von die Entfernung ($r$), was durch der Verson ($\hat{r}$) dargestellt werden kann. Daher wird das Gesetz wie folgt ausgedrückt:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ q Q }{ r ^2} \hat{r} $ |
Wenn die Entfernung ($r$) als der Abstand zwischen die Position 1 ($\vec{s}_1$) und die Position 2 ($\vec{s}_2$) betrachtet wird, kann dies wie folgt ausgedrückt werden:
| $ r =| \vec{s}_2 - \vec{s}_1 |$ |
und für der Verson ($\hat{r}$) gilt:
| $ \hat{r} =\displaystyle\frac{( \vec{s}_2 - \vec{s}_1 )}{| \vec{s}_2 - \vec{s}_1 |}$ |
Indem die Position ($\vec{r}$) mit die Position 2 ($\vec{s}_2$), die Position 1 ($\vec{s}_1$) mit die Position einer Ladung i ($\vec{u}_i$) und die Ladung ($Q$) mit die Ladung der Ionen i ($Q_i$) assoziiert werden, kann man schließen, dass die gesamte die Kraft ($\vec{F}$) ist:
| $ \vec{F} =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\sum_i^N\displaystyle\frac{ q Q_i }{| \vec{r} - \vec{u}_i |^3}( \vec{r} - \vec{u}_i )$ |
ID:(10392, 0)