Druyd:Knowledge

Solución General

Storyboard

>Modelo

ID:(749, 0)

Amortiguación de oscilación

Definición

Ecuación de solución general

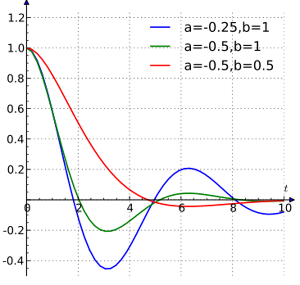
Oscilación amortiguada

ID:(2698, 0)

Niña en columpio como ejemplo de resonancia

Imagen

Si una persona se columpia procede a impulsarse con los pies y el cuerpo en un ritmo que en general corresponde a la frecuencia del columpio.

Niña columpiandose

Esto es porque el proceso es resonante, es decir en cada ciclo agrega energía en el mismo ritmo que oscila.

ID:(1650, 0)

Oscilación con amplitud creciente

Nota

En el caso de que el proceso es resonante, la amplitud crece exponencialmente:

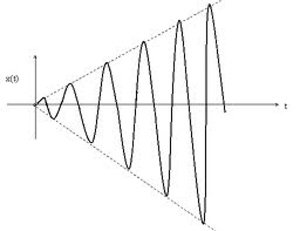
Caso de crecimiento resonante

ID:(1651, 0)

Equilibrio sobre cuerda floja

Cita

La clave de lograr controlar el proceso es que el retraso de la reacción a una perturbación sea tal que el proceso se logre amortiguar esta y que las correcciones no terminen desestabilizando el proceso. Esto en el caso de la persona en la cuerda floja es tan clave como diferenciar vida y muerte.

Equilibrio sobre cuerda floja

ID:(2699, 0)

No existencia de una solución de armónicos

Ejercicio

Como ya vimos existe la posibilidad de que no exista una solución con una componente oscilante (armónica) de la forma como hemos planteado. En este caso el sistema,a realiza una dinámica más compleja que por lo general requiere de una solución numérica para poder estudiarla. En muchos casos la solución 'oscila' entre una solución del tipo convergente y una divergente. Esto significa que una perturbación por momentos esta siendo controlada y tiempo después igual perdemos el control.

ID:(83, 0)

Solución General

Storyboard

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$x$

Amplitud

$\lambda$

lam

Factor de Amortiguación

1/s

$f$

Factor de Amplificación

1/s

$\phi$

phi

Fase

$\omega$

omega

Frecuencia angular de la regulación

rad/s

$p_t$

p_t

Función de respuesta

$G(t)$

Perturbación

1/s

$t$

Tiempo

$\tau$

tau

Tiempo de reacción

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$p(t)=p_0e^{-\lambda t}\cos(\omega t + \phi)$

p(t)=p_0e^{-\lambda t}\cos(\omega t + \phi)

$(-\lambda+ge^{\lambda\tau}\cos\omega\tau)cos(\omega t+\phi)+(-\omega+ge^{\lambda\tau}\sin\omega\tau)sin(\omega t+\phi)+\displaystyle\frac{1}{p_0}G(t)e^{\lambda t}=0$

(- lambda + g * exp( lambda * tau )*cos( omega * tau )*cos( omega * t + phi )+(- omega + g * exp( lambda * tau )*sin( omega * tau )*sin( omega * t + phi )+(1/ p_0 )* G * exp( lambda * t )=0

$\omega>g$

omega>g

$\lambda^2+\omega^2=g^2 e^{2\lambda\tau}$

lambda^2+omega^2=g^2*e^(2*lambda*tau)

$\lambda=g e^{\lambda\tau}\cos\omega\tau$

lambda=g e^(lambda*tau)*cos(omega*tau)

$\omega=-g e^{\lambda\tau}\sin\omega\tau$

omega=-g*e^(lambda*tau)*sin(omega*tau)

Ejemplos

Ansatz para soluci n general

Si la ecuaci n de control tiene la forma

equation=4648

y la perturbaci n G(t) tiene la forma de una oscilaci n de frecuencia angular \omega

equation

donde \phi es la fase, el factor de relajamiento \lambda y p_0 la amplitud.

Las soluciones pueden ser

- convergentes ($\lambda$ > 0)

- divergentes ($\lambda$ < 0)

- oscilantes ($\lambda$ = 0)

Soluci n general

Con el ansatz

equation=4650

en la ecuaci n

equation=3173

pero en su versi n que incluye el desface

\displaystyle\frac{dp}{dt}+gp(t-\tau)=G(t)

se obtiene la ecuaci n:

equation

Primera ecuaci n

Como la ecuaci n

equation=4651

debe ser valida para todo tiempo t se tiene que debe ser:

equation

Segunda ecuaci n

Como la ecuaci n

equation=4651

debe ser valida para todo tiempo t se tiene que debe ser:

equation

Ecuaci n de estabilidad

Como vale que

equation=4656

y

equation=4657

si ambas ecuaciones se cuadran y suman se tiene que debe cumplirse:

equation

Condici n de estabilidad

Para que exista una soluci n se debe dar que \omega debe superar g de modo que

equation=4653

tenga siempre una soluci n para alg n \lambda, o sea

equation

Amortiguaci n de oscilaci n

Ecuaci n de soluci n general

image

Ni a en columpio como ejemplo de resonancia

Si una persona se columpia procede a impulsarse con los pies y el cuerpo en un ritmo que en general corresponde a la frecuencia del columpio.

image

Esto es porque el proceso es resonante, es decir en cada ciclo agrega energ a en el mismo ritmo que oscila.

Oscilaci n con amplitud creciente

En el caso de que el proceso es resonante, la amplitud crece exponencialmente:

image

Equilibrio sobre cuerda floja

La clave de lograr controlar el proceso es que el retraso de la reacci n a una perturbaci n sea tal que el proceso se logre amortiguar esta y que las correcciones no terminen desestabilizando el proceso. Esto en el caso de la persona en la cuerda floja es tan clave como diferenciar vida y muerte.

image

No existencia de una soluci n de arm nicos

Como ya vimos existe la posibilidad de que no exista una soluci n con una componente oscilante (arm nica) de la forma como hemos planteado. En este caso el sistema,a realiza una din mica m s compleja que por lo general requiere de una soluci n num rica para poder estudiarla. En muchos casos la soluci n 'oscila' entre una soluci n del tipo convergente y una divergente. Esto significa que una perturbaci n por momentos esta siendo controlada y tiempo despu s igual perdemos el control.

>Modelo

ID:(749, 0)