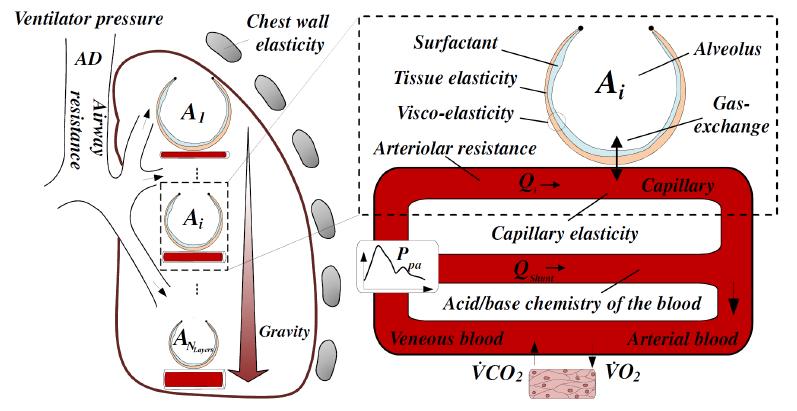
Modelo del Pulmon
Description 
Variables
Calculations
Calculations
Equations
None
(ID 4731)
(ID 7615)
(ID 7616)
Examples
lung004
(ID 7365)
(ID 7349)
(ID 7622)
La superficie de una esfera es con igual a
| $ S = 4 \pi r ^2$ |
(ID 4731)
$S_t=NS$
(ID 7615)
La tensi n superficial act a en funci n de deformaciones que ocurran a la superficie. Por ello, esta es una funci n del rea actual $A_{alv,i}$ y aquella que exist a antes de deformarse $A_{0,i}$. Por este motivo se puede introducir una superficie alveolar relativa como
$A_r=\displaystyle\frac{A_{alv,i}}{A_{0,i}}$
(ID 7357)
$V_t=NV$
(ID 7616)
La presi n elastica act a en funci n de deformaciones que ocurran en el volumen. Por ello, esta es una funci n del rea actual $V_{alv,i}$ y aquella que exist a antes de deformarse $V_{max,i}$. Por este motivo se puede introducir una superficie alveolar relativa como
$V_r=\displaystyle\frac{V_{alv,i}}{V_{max,i}}$
(ID 7360)
El volumen maximo del alveolo se calcula de la capacidad maxima $TLC$ restando el volumen muerto $V_{ad}$ y dividiendo por el numero de alveolos:
$V_{alv,max}=\displaystyle\frac{TLC-V_{ad}}{N_{alv,i}}$
(ID 7361)

lung001
(ID 7362)
El volumen m ximo que puede exhalar una persona en forma forzada (MEFV) se ha modelado siendo uno de los mejores modelos el de Adam G. Polak de 1998. El modelo da una relaci n entre la presi n y volumen logrado de la forma
$P_d(V)=P_m(1-e^{-t/\tau))\left(1-\displaystyle\frac{V}{VC}\right)-R_TQ$
donde $P_m$ es la presi n m xima generada por m sculos y fuerzas el sticas del tejido del t rax, $VC$ es la capacidad pulmonar, $\tau$ el tiempo de relajamiento, $R_T$ la resistencia del tejido y $Q$ el flujo de aire.
Adam G.Polak. A forward model for maximum expiration. Computers in Biology and Medicine 1998; 28: 613-625.
(ID 7350)
La presi n $P_{\gamma,i}$ generada por la tensi n superficial de los alv olos depende de la tensi n superficial $\gamma$ en si y el radio del alv olo $r_i$ en el nivel $i$:
$P_{\gamma,i}=\displaystyle\frac{2\gamma}{r_i}$
(ID 7355)
La tensi n superficial del aleveolo ha sido medida siendo una funci n de la superficie alveolar relativa $A_r$ asumiendo el valor:
$\gamma=(197.2 A_r^2-248.5 A_r+79.3)mN/m$
(ID 7358)

lung007
(ID 7368)
La presi n de la pared tor cica $P_{cw}$ ha sido medida y se ha mostrado que depende de la relaci n del volumen total $V_t$ y la capacidad $TLC$ siendo
$P_{cw}=P_{cw0}-P_{cw1}\ln\left(\displaystyle\frac{0.95}{\displaystyle\frac{V_t}{TLC}-0.22}-1\rigth)$
donde los factores $P_{cw0}$ es $0.71,kPa$ y $P_{cw1}$ es $0.58,kPa$.
(ID 7620)

lung008
(ID 7369)
La presi n elastica del aleveolo ha sido medida siendo una funci n de volumen relativo $V_r$ asumiendo el valor:
$P_e=(0.42-0.22 ln\left(\displaystyle\frac{1}{0.98 V_r+0.015}-1\right)kPa$
(ID 7359)

lung006
(ID 7367)
La presi n en el alveolo $P_{alv}$ del nivel $i$ se suma de la presi n de la tensi n superficial del alveolo $P_{\gamma,i}$, de la presi n generada por la elasticidad de la pared del alv lo $P_{e,i}$, por la presi n de las paredes $P_{cw}$ y por la presi n hidrostaica $P_{h,i}$:
$P_{alv}=P_{\gamma,i}+P_{e,i}+P_{cw}+P_{h,i}$
(ID 7354)

lung005
(ID 7366)
La pared entre el espacio interior del alv olo y los vasos sangu neos es de solo un micron facilitando la difusi n de las mol culas de oxigeno y di xido de carb n. El volumen que logra migrar $\Delta V$ es proporcional a la diferencia de presi n $\Delta p$ que existe entre el espacio interior del alv olo y la sangre:
$C=\displaystyle\frac{\Delta V}{\Delta p}$
La constante es del orden de $0.1,l/cmH2O$.
(ID 7621)

lung002
(ID 7363)

lung003
(ID 7364)
Dentro del modelo el ctrico la resistencia se puede modelar en funci n de par metros de la din mica de flujo de gases, resultando
$r_a=\displaystyle\frac{8\mu l}{\rho_0\pi R_t^4}$
donde $\mu$ es la viscosidad del aire, $\rho_0$ la densidad de este, $l$ el largo y $R_t$ el radio del alv olo.
(ID 7352)
Dentro del modelo el ctrico la capacidad se puede modelar en funci n de par metros de la din mica de flujo de gases, resultando
$c_a=\displaystyle\frac{V}{\rho_0c_o^2}$
donde $V$ es el del alv olo, $\rho_0$ la densidad del aire y $c_0$ la velocidad de propagaci n.
(ID 7351)
Dentro del modelo el ctrico la inductancia se puede modelar en funci n de par metros de la din mica de flujo de gases, resultando
$l_a=\displaystyle\frac{\rho_0l}{S}$
donde $\rho_0$ es la densidad del aire, $l$ el largo y $S$ la secci n del alv olo.
(ID 7353)
ID:(730, 0)
