Usuario:
Modelos de falanges
Definición 
Si observamos la estructura de un dedo vemos que consta de un total de cuatro falanges en donde la primera se encuentra en la zona de la palma de la mano:
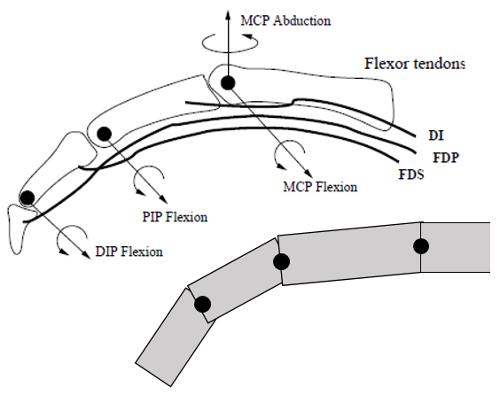
Modelo de la mano con múltiples cilindros representando las falanges
La movilidad general son las articulaciones en torno a un eje perpendicular a todas las falanges. Solo entre la primera y segunda falange existe una posibilidad de rotación en torno a un eje perpendicular a la palma de la mano.
Este esquema se repite para todos los dedos incluyendo el pulgar.
ID:(2695, 0)
Fuerza en una falange
Imagen
Modelo mecánico de la falange puede ser comprendido como un elemento con un centro de masa 'O' largo
En los dos extremos A y B actúan las fuerzas
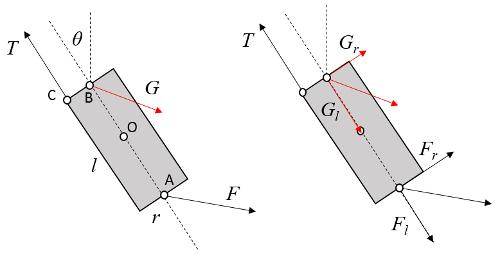
Diagrama de las fuerzas que actúan sobre una falange
El proceso de calculo se puede resumir en las siguientes etapas:
en donde:
ID:(2696, 0)
Acción y reacción
Nota
Etapa:
Para que el centro de masa no se desplace, la fuerzas
o sea
ID:(4642, 0)
Fuerza sobre la falange
Cita
Etapa:
La fuerza que actúa sobre el dedo como reacción a la fuerza que realizamos al manipular un objeto se puede expresar ya sea en coordenadas cartesianas
ID:(1346, 0)
Fuerza sobre la falange, anterior
Ejercicio
Etapa:
La falange actúa sobre la falange anterior que debe aportar la fuerza necesaria para estabilizarla. Esta la denominaremos
Para que el centro de masa no se desplace es necesario que las fuerzas radiales se compensen, es decir
Lo mismo se exige a las fuerzas en dirección del eje del dedo:
De igual forma se debe anular los torques por lo que
ID:(1347, 0)
Modelo de la Falange
Storyboard
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Dado que la relaci n con la fuerza de acción ($F_A$) y la fuerza de reacción ($F_R$) en una dimensi n es
se puede aplicar a cada componente de la fuerza de acción (vector) ($\vec{F}_A$) y la fuerza de reacción (vector) ($\vec{F}_R$), lo que resulta en
$\vec{F}R=(F{Rx},F_{Ry},F_{Rz})=(-F_{Ax},-F_{Ay},-F_{Az})=-\vec{F}_A$
Por lo tanto,
Ejemplos
Si observamos la estructura de un dedo vemos que consta de un total de cuatro falanges en donde la primera se encuentra en la zona de la palma de la mano:
La movilidad general son las articulaciones en torno a un eje perpendicular a todas las falanges. Solo entre la primera y segunda falange existe una posibilidad de rotaci n en torno a un eje perpendicular a la palma de la mano.
Este esquema se repite para todos los dedos incluyendo el pulgar.
Modelo mec nico de la falange puede ser comprendido como un elemento con un centro de masa 'O' largo
En los dos extremos A y B act an las fuerzas
El proceso de calculo se puede resumir en las siguientes etapas:
en donde:
Etapa:
Para que el centro de masa no se desplace, la fuerzas
o sea
Etapa:
La acci n de una falange
lo que en la direcci n
Etapa:
La acci n de una falange
lo que en la direcci n
Etapa:
La fuerza que act a sobre el dedo como reacci n a la fuerza que realizamos al manipular un objeto se puede expresar ya sea en coordenadas cartesianas
Etapa:
Con las fuerzas en los ejes de la falange
Etapa:
Con las fuerzas en los ejes de la falange
Etapa:
Con la fuerza
donde
Etapa:
Con la fuerza
donde
Etapa:
La falange act a sobre la falange anterior que debe aportar la fuerza necesaria para estabilizarla. Esta la denominaremos
Para que el centro de masa no se desplace es necesario que las fuerzas radiales se compensen, es decir
Lo mismo se exige a las fuerzas en direcci n del eje del dedo:
De igual forma se debe anular los torques por lo que
Etapa:
Para compensar el torque
por lo que
Etapa:
Para que el centro de masa no se desplace es necesario que las fuerzas radiales se compensen,
es decir
Etapa:
Para que el dedo se mantenga y no rote el torque total debe ser nulo,
es decir
por lo que la componente
Cuando un cuerpo esta en equilibrio su centro de masa no se esta desplazando. Para ello la suma de las fuerzas sobre este deben ser nula o sea con
Cuando un cuerpo est en equilibrio con respecto a la rotaci n, no gira alrededor de su centro de masa. Para lograrlo, la suma de los momentos de torsi n sobre el cuerpo debe ser cero. Esto implica que:
La relaci n entre la fuerza de acción ($F_A$) y la fuerza de reacción ($F_R$) unidimensional
se puede generalizar para m s dimensiones con la fuerza de acción (vector) ($\vec{F}_A$) y la fuerza de reacción (vector) ($\vec{F}_R$) como
ID:(65, 0)