Translation
Definition 
Die Basis der Mechanik besteht darin, die Position
Die Translation bezieht sich auf die Bewegung eines Objekts im Laufe der Zeit, was zu einer Änderung seiner Position
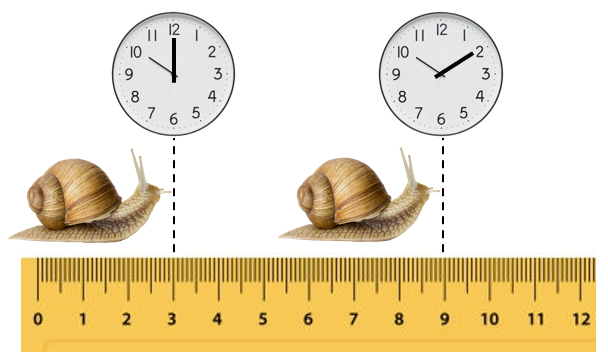
Durch die Festlegung einer Funktion für die Position eines Objekts im Laufe der Zeit wird es möglich, dessen zukünftige Bewegung und Bahn im Laufe der Zeit vorherzusagen.
ID:(466, 0)
Durchschnittsgeschwindigkeit
Bild 
Um zu schätzen, wie sich ein Objekt bewegt, müssen wir den Weg-Zeit-Verlauf kennen. Daher wird das Verhältnis zwischen dem zurückgelegten Weg und der vergangenen Zeit als Durchschnittsgeschwindigkeit definiert.
Um die Messung durchzuführen, kann ein System wie das in der Abbildung verwendet werden:
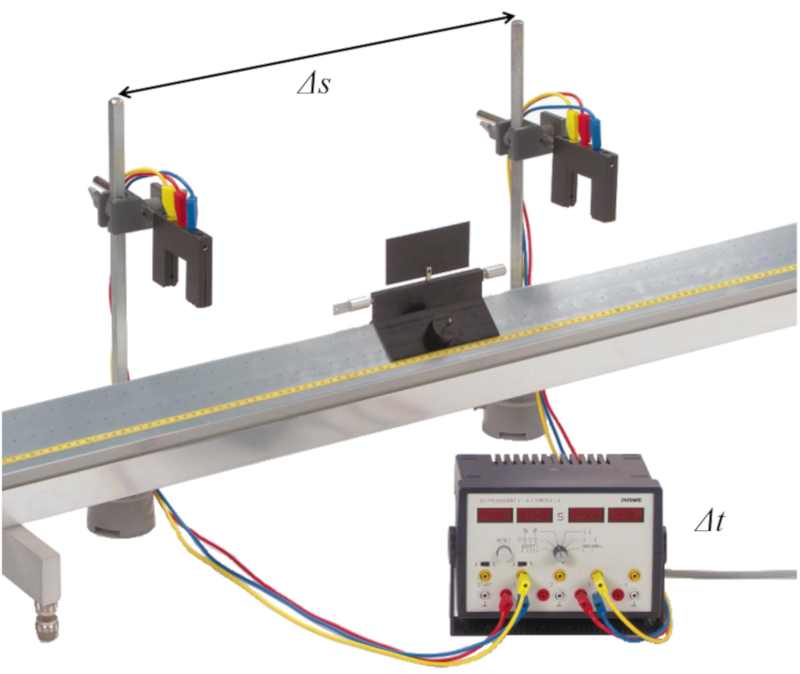
Um die Durchschnittsgeschwindigkeit zu bestimmen, müssen zwei Sensoren platziert werden, die den Durchgang eines Objekts in einem Abstand $\Delta s$ registrieren. Dann wird der Zeitunterschied registriert, wenn das Objekt jeden Sensor passiert $\Delta t$. Mit beiden Werten wird die Durchschnittsgeschwindigkeit bestimmt, indem die zurückgelegte Entfernung durch die vergangene Zeit dividiert wird.
Die Gleichung, die die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) beschreibt, lautet wie folgt:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Es ist zu beachten, dass die Durchschnittsgeschwindigkeit eine Schätzung der tatsächlichen Geschwindigkeit ist. Das Hauptproblem liegt darin, dass:
Wenn sich die Geschwindigkeit während der vergangenen Zeit ändert, kann der Wert der Durchschnittsgeschwindigkeit sehr unterschiedlich von einer Durchschnittsgeschwindigkeit sein.
Zusätzlich gibt es ein Problem bei der Messung der zurückgelegten Entfernung, da mit zwei Positionen gearbeitet wird. Dies kann dazu führen, dass
Da der zurückgelegte Weg aus der Differenz zweier Positionen berechnet wird, kann es passieren, dass sich die Anfangs- und Endposition im Falle einer Bewegungsumkehr während der vergangenen Zeit sehr ähnlich sind. Dies kann zu einer Durchschnittsgeschwindigkeit führen, die annähernd null ist, obwohl ein \\\\\"langer\\\\\" Weg zurückgelegt wurde.
Deshalb ist der Schlüssel,
Die Geschwindigkeit in einer ausreichend kurzen vergangenen Zeit zu bestimmen, damit ihre Änderung minimal ist.
ID:(470, 0)
Augenblickliche Geschwindigkeit
Notiz 
Die Geschwindigkeit ($v$) wird als die Verlagerung pro Zeiteinheit definiert. Dieses Konzept reduziert sich jedoch auf eine Mittlere Geschwindigkeit ($\bar{v}$), das während des betrachteten Zeitintervalls existiert.
Die Begrenztheit der Durchschnittsgeschwindigkeit zeigt sich darin, dass angenommen wird, dass ein Objekt sofort von Ruhe in eine gegebene Geschwindigkeit übergeht. Es ist, als würde ein Bus sofort nach dem Verlassen seines Terminals eine Reisegeschwindigkeit erreichen, was völlig absurd ist. Die Geschwindigkeit entwickelt sich, nimmt zu, nimmt ab (Ampel, Fahrgäste steigen ein) und steigt langsam an, bis sie einen mehr oder weniger konstanten Wert erreicht, wenn sie auf der Straße fährt. Auf diese Weise wird ein Bus, der normalerweise mit etwa 100 km/h auf der Straße fährt, mehr als 8 Stunden brauchen, um 800 km zurückzulegen, da die Geschwindigkeitsfluktuationen berücksichtigt werden müssen. Am Ende wird er 10 Stunden für 800 km gebraucht haben und mit einer Durchschnittsgeschwindigkeit von 80 km/h gefahren sein.
Wenn man die Geschwindigkeit zu jedem Zeitpunkt kennen möchte, muss man eine so kleine Zeit wählen, dass während dieser Zeit die Geschwindigkeit annähernd konstant sein kann. Dadurch entspricht die auf diese Weise geschätzte Durchschnittsgeschwindigkeit der Geschwindigkeit, die zum betreffenden Zeitpunkt existiert.
Deshalb sprechen wir von der momentanen Geschwindigkeit.
ID:(16, 0)
Zeitpfaddiagramm für konstante Geschwindigkeit ohne Anfangszeit
Zitat 
Für den Fall einer konstanten Geschwindigkeit ohne Anfangszeit kann die Position mit berechnet werden:
| $ s_v = s_0 + v_0 t $ |
Das entspricht einer Geraden mit:
• Steigung gleich der Geschwindigkeit $v_0$
• Anfangsposition $x_0$
wie unten dargestellt:
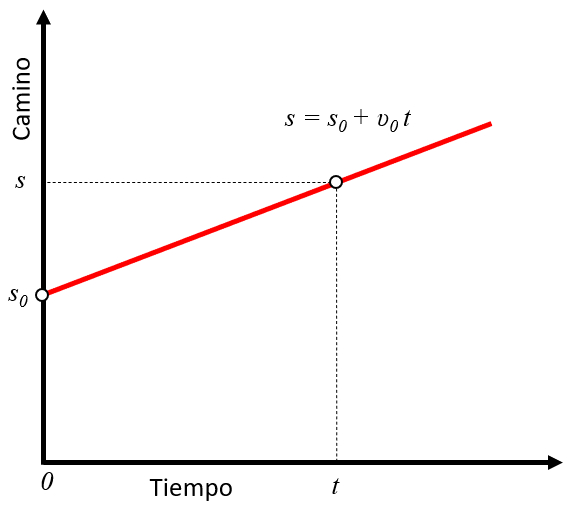
ID:(2244, 0)
Zeitpfaddiagramm für konstante Geschwindigkeit und Anfangszeit
Übung 
Für den Fall einer konstanten Geschwindigkeit und eines Anfangszeitpunkts kann die Position mit den Werten die Position ($s$), die Ausgangsstellung ($s_0$), die Konstante Geschwindigkeit ($v_0$), der Zeit ($t$) und der Startzeit ($t_0$) mithilfe der folgenden Gleichung berechnet werden:
| $ s = s_0 + v_0 ( t - t_0 )$ |
Die Gleichung entspricht einer geraden Linie mit:
• einer Steigung von die Konstante Geschwindigkeit ($v_0$)
• einem y-Achsenabschnitt bei die Ausgangsstellung ($s_0$) für der Startzeit ($t_0$)
wie unten dargestellt:
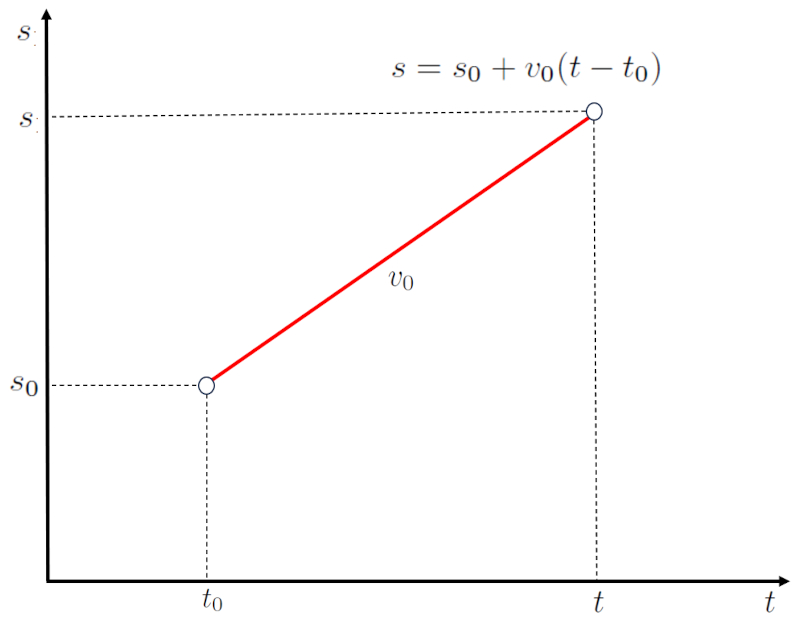
ID:(2243, 0)
Paradoxon des Körpers in Ruhe
Gleichung 
Wenn sich ein Körper im "Ruhezustand" befindet, bedeutet dies, dass er im Ruhezustand bezüglich unseres Bezugssystems oder Koordinatensystems ist. Dieser "Ruhezustand" ist jedoch völlig relativ, das heißt, von einem Körper aus, der sich relativ zu unserem System bewegt, ist der "ruhende" Körper auch in Bewegung.
In diesem Sinne gibt es keinen "absoluten Ruhezustand", sondern nur einen relativ zum jeweiligen Bezugssystem. Deshalb ist im Allgemeinen jede Geschwindigkeitsmessung eine Messung im Verhältnis zu einem bestimmten Bezugssystem.
Wenn sich ein Körper zum Beispiel sehr langsam zu bewegen scheint, bedeutet dies nur, dass seine Geschwindigkeit der Geschwindigkeit des Bezugssystems, in dem die langsame Bewegung beobachtet wird, sehr ähnlich ist.
ID:(4405, 0)
Geschwindigkeit als Ableitung
Script 
Wenn wir ein Zeit ($t$) mit eine Position ($s$) ($s(t)$) nehmen und einen Punkt zu einer zukünftigen Zeit $t+\Delta t$ mit einer Position $s(t+\Delta t)$ betrachten, können wir die Geschwindigkeit als die Strecke im Zeitintervall $\Delta t$ abschätzen:
$s(t+\Delta t)-s(t)$
die Geschwindigkeit ($v$) kann berechnet werden, indem man die zurückgelegte Strecke durch die vergangene Zeit teilt:
$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$
Wenn der Wert von $\Delta t$ kleiner wird, nähert sich die berechnete Geschwindigkeit der Tangente an die Positionscurve zur Zeit:
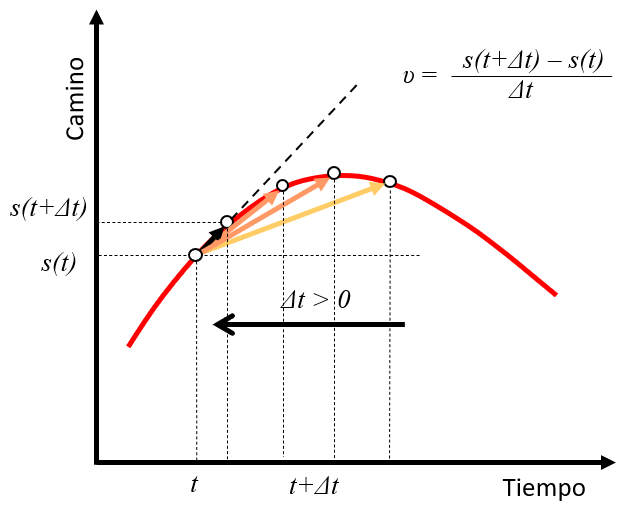
Dies verallgemeinert das, was bereits für den Fall konstanter Geschwindigkeit gesehen wurde.
ID:(1638, 0)
Geschwindigkeit als Steigung der Positionskurve
Variable 
Wenn die Verschiebung als eine Linie zwischen dem Ursprung O und dem Punkt A dargestellt wird:
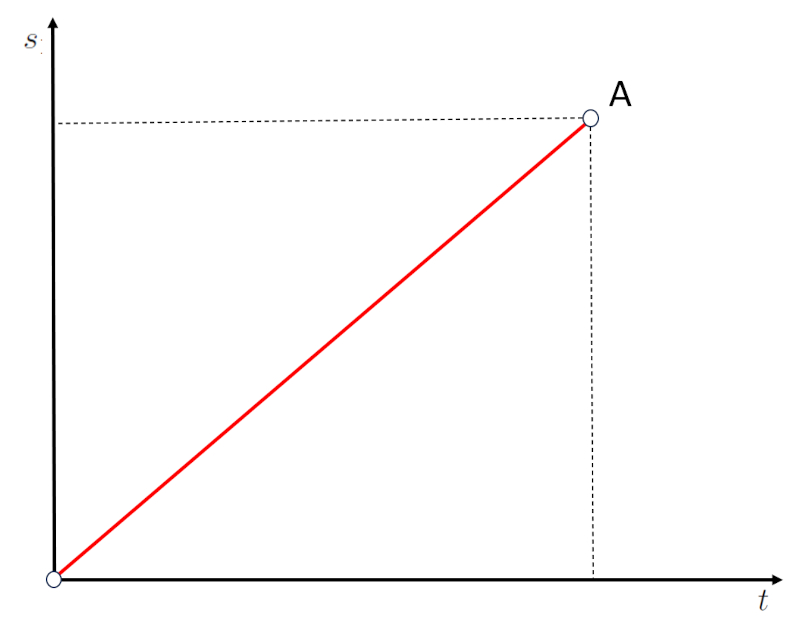
Sieht man, dass eine Strecke in einer bestimmten Zeit zurückgelegt wurde. Daher entspricht die Steigung der Grafik Strecke vs. Zeit der Geschwindigkeit.
Wenn die Steigung größer ist, bedeutet dies, dass eine Strecke in kürzerer Zeit zurückgelegt wird, was einer höheren Geschwindigkeit entspricht.
Wenn die Steigung kleiner ist, bedeutet dies, dass eine Strecke in längerer Zeit zurückgelegt wird, was einer niedrigeren Geschwindigkeit entspricht.
ID:(2239, 0)
Negative Steigung
Audio 
Im Fall eines Graphen mit einem Abschnitt negativer Steigung:
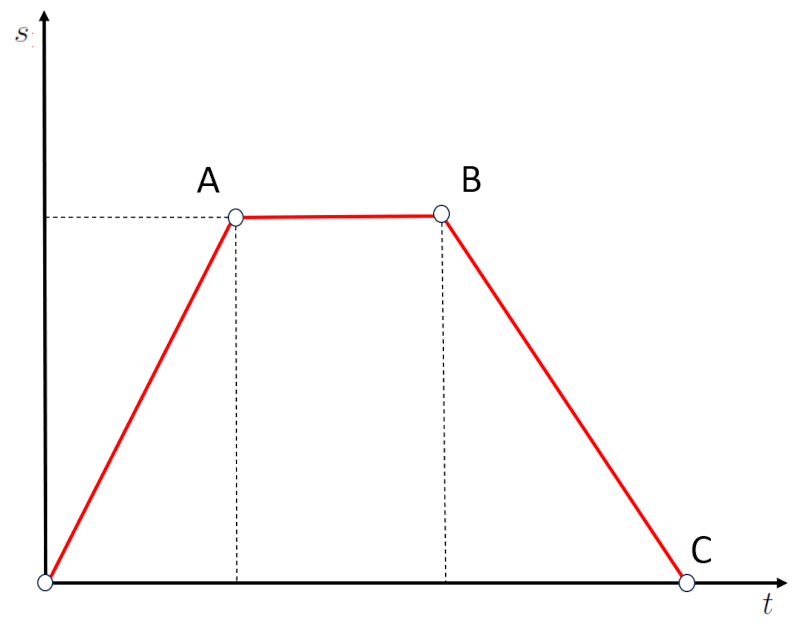
Liegt eine Situation vor, in der man von der Position B zur Position C zurückgekehrt ist, die sich in einer Entfernung von Null befindet. Mit anderen Worten, negative Steigungen bedeuten, dass man sich in die entgegengesetzte Richtung bewegt, nicht weg vom Ursprung, sondern auf ihn zu.
ID:(2245, 0)
Weg als Integral der Geschwindigkeit
Video 
Das Integral von die Geschwindigkeit ($v$) entspricht dem Bereich unter der Kurve, die diese Funktion definiert. Daher entspricht das Integral der Geschwindigkeit zwischen der Startzeit ($t_0$) und der Zeit ($t$) der zurückgelegten Strecke zwischen die Ausgangsstellung ($s_0$) und die Position ($s$).
Deshalb haben wir:
| $ s = s_0 +\displaystyle\int_{t_0}^t v d\tau$ |
Was in der folgenden Grafik dargestellt ist:
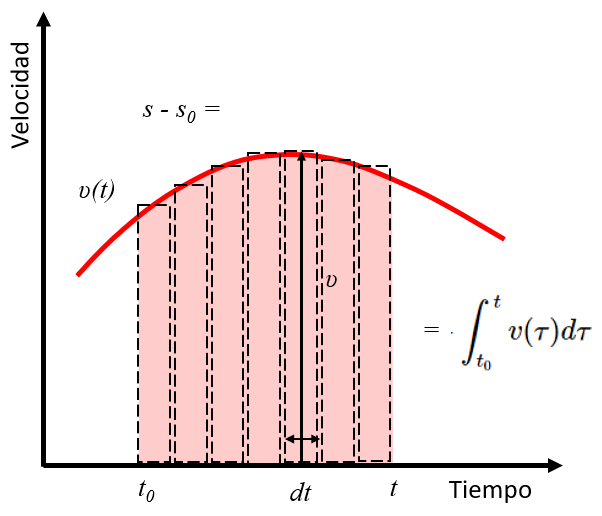
Ich gehe als Bereich unter der Geschwindigkeits- und Zeitkurve.
ID:(2242, 0)
Zeitpfaddiagramm mit horizontalem Segment
Einheit 
Ein zweiter Fall sind horizontale Abschnitte im Weg-Zeit-Diagramm:
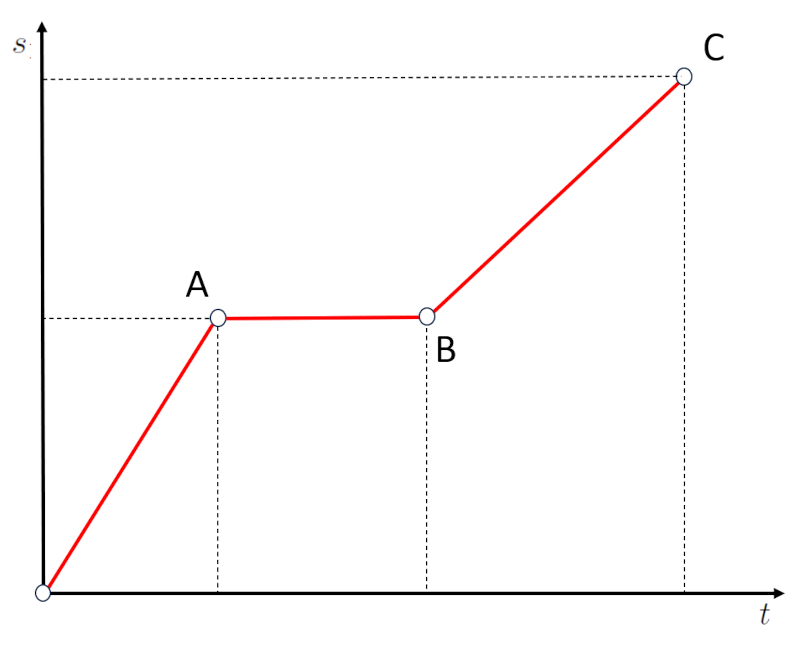
Wenn wir uns den Abschnitt AB ansehen, werden wir feststellen, dass sich der Weg trotz verstrichener Zeit nicht verändert hat. Das bedeutet, dass das Objekt angehalten ist. Daher entsprechen horizontale Abschnitte, die einer Nullsteigung entsprechen, Phasen, in denen die Geschwindigkeit null ist.
ID:(2241, 0)
Geschwindigkeit in mehr als einer Dimension
Code 
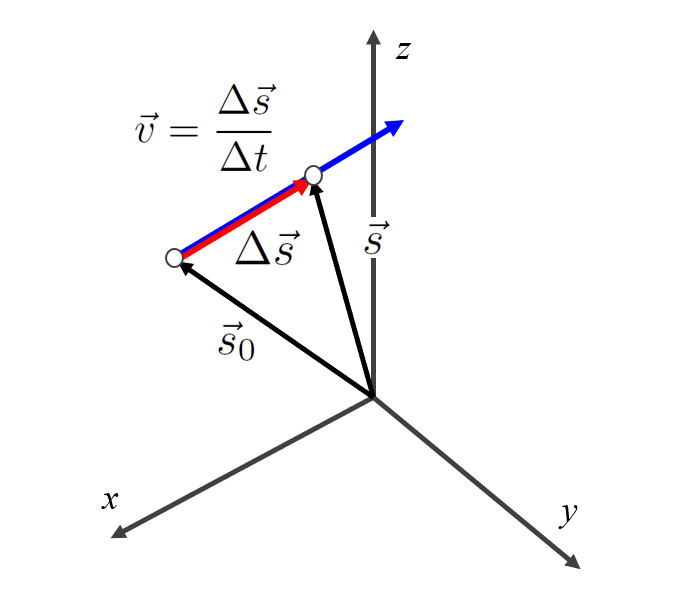
Die Geschwindigkeit eines Objekts in einem System mit mehr als einer Dimension wird traditionell durch einen Vektor definiert. Dieser Vektor hat seinen Ursprung am Objekt und ist in Richtung der Bewegung des Objekts orientiert.
ID:(2240, 0)
Konzepte
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
Wenn wir den zur ckgelegten Weg als die Differenz der Positionen zwischen der Zeit $t+\Delta t$ und der Zeit $t$ betrachten:
$\Delta s = s(t+\Delta t)-s(t)$
und $\Delta t$ als die vergangene Zeit nehmen, dann kann die durchschnittliche Geschwindigkeit im Grenzwert infinitesimal kurzer Zeiten ausgedr ckt werden als:
$v_m=\displaystyle\frac{\Delta s}{\Delta t}=\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}=\displaystyle\frac{ds}{dt}$
Dieser letzte Ausdruck entspricht der Ableitung der Positionsxadfunktion $s(t)$:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
die wiederum die Steigung der graphischen Darstellung dieser Funktion ber der Zeit ist.
(ID 3153)
Mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) gleich die Position ($s$) und die Ausgangsstellung ($s_0$):
| $ \Delta s = s_2 - s_1 $ |
und der Abgelaufene Zeit ($\Delta t$) ist gleich der Zeit ($t$) und der Startzeit ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
Die Gleichung f r die durchschnittliche Geschwindigkeit:
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
kann geschrieben werden als:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
somit ergibt sich, wenn man nach ihr aufl st:
| $ s = s_0 + v_0 ( t - t_0 )$ |
(ID 3154)
Da die Geschwindigkeit ein Vektor ist, kann sie als ein Array ihrer verschiedenen Komponenten ausgedr ckt werden:
$\vec{v}=\begin{pmatrix}v_x\v_y\v_z\end{pmatrix}$
Ihre Ableitung kann als die Ableitung jeder ihrer Komponenten ausgedr ckt werden:
$\displaystyle\frac{d\vec{v}}{dt}=\begin{pmatrix}\displaystyle\frac{d v_x}{dt}\displaystyle\frac{d v_y}{dt}\displaystyle\frac{d v_z}{dt}\end{pmatrix}=\begin{pmatrix}a_x\a_y\a_z\end{pmatrix}=\vec{a}$
Daher ist die instantane Geschwindigkeit im Allgemeinen in mehr als einer Dimension ein Vektor mit Komponenten in jeder Richtung:
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
(ID 4354)
Beispiele
Die Basis der Mechanik besteht darin, die Position
Die Translation bezieht sich auf die Bewegung eines Objekts im Laufe der Zeit, was zu einer nderung seiner Position

Durch die Festlegung einer Funktion f r die Position eines Objekts im Laufe der Zeit wird es m glich, dessen zuk nftige Bewegung und Bahn im Laufe der Zeit vorherzusagen.
(ID 466)
Um zu sch tzen, wie sich ein Objekt bewegt, m ssen wir den Weg-Zeit-Verlauf kennen. Daher wird das Verh ltnis zwischen dem zur ckgelegten Weg und der vergangenen Zeit als Durchschnittsgeschwindigkeit definiert.
Um die Messung durchzuf hren, kann ein System wie das in der Abbildung verwendet werden:

Um die Durchschnittsgeschwindigkeit zu bestimmen, m ssen zwei Sensoren platziert werden, die den Durchgang eines Objekts in einem Abstand $\Delta s$ registrieren. Dann wird der Zeitunterschied registriert, wenn das Objekt jeden Sensor passiert $\Delta t$. Mit beiden Werten wird die Durchschnittsgeschwindigkeit bestimmt, indem die zur ckgelegte Entfernung durch die vergangene Zeit dividiert wird.
Die Gleichung, die die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) beschreibt, lautet wie folgt:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Es ist zu beachten, dass die Durchschnittsgeschwindigkeit eine Sch tzung der tats chlichen Geschwindigkeit ist. Das Hauptproblem liegt darin, dass:
Wenn sich die Geschwindigkeit w hrend der vergangenen Zeit ndert, kann der Wert der Durchschnittsgeschwindigkeit sehr unterschiedlich von einer Durchschnittsgeschwindigkeit sein.
Zus tzlich gibt es ein Problem bei der Messung der zur ckgelegten Entfernung, da mit zwei Positionen gearbeitet wird. Dies kann dazu f hren, dass
Da der zur ckgelegte Weg aus der Differenz zweier Positionen berechnet wird, kann es passieren, dass sich die Anfangs- und Endposition im Falle einer Bewegungsumkehr w hrend der vergangenen Zeit sehr hnlich sind. Dies kann zu einer Durchschnittsgeschwindigkeit f hren, die ann hernd null ist, obwohl ein \\\\\"langer\\\\\" Weg zur ckgelegt wurde.
Deshalb ist der Schl ssel,
Die Geschwindigkeit in einer ausreichend kurzen vergangenen Zeit zu bestimmen, damit ihre nderung minimal ist.
(ID 470)
Die Geschwindigkeit ($v$) wird als die Verlagerung pro Zeiteinheit definiert. Dieses Konzept reduziert sich jedoch auf eine Mittlere Geschwindigkeit ($\bar{v}$), das w hrend des betrachteten Zeitintervalls existiert.
Die Begrenztheit der Durchschnittsgeschwindigkeit zeigt sich darin, dass angenommen wird, dass ein Objekt sofort von Ruhe in eine gegebene Geschwindigkeit bergeht. Es ist, als w rde ein Bus sofort nach dem Verlassen seines Terminals eine Reisegeschwindigkeit erreichen, was v llig absurd ist. Die Geschwindigkeit entwickelt sich, nimmt zu, nimmt ab (Ampel, Fahrg ste steigen ein) und steigt langsam an, bis sie einen mehr oder weniger konstanten Wert erreicht, wenn sie auf der Stra e f hrt. Auf diese Weise wird ein Bus, der normalerweise mit etwa 100 km/h auf der Stra e f hrt, mehr als 8 Stunden brauchen, um 800 km zur ckzulegen, da die Geschwindigkeitsfluktuationen ber cksichtigt werden m ssen. Am Ende wird er 10 Stunden f r 800 km gebraucht haben und mit einer Durchschnittsgeschwindigkeit von 80 km/h gefahren sein.
Wenn man die Geschwindigkeit zu jedem Zeitpunkt kennen m chte, muss man eine so kleine Zeit w hlen, dass w hrend dieser Zeit die Geschwindigkeit ann hernd konstant sein kann. Dadurch entspricht die auf diese Weise gesch tzte Durchschnittsgeschwindigkeit der Geschwindigkeit, die zum betreffenden Zeitpunkt existiert.
Deshalb sprechen wir von der momentanen Geschwindigkeit.
(ID 16)
Die Mittlere Geschwindigkeit ($\bar{v}$) kann aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) berechnet werden mit:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
(ID 3152)
Im Allgemeinen muss die Geschwindigkeit als eine dreidimensionale Einheit verstanden werden, also als Vektor. Ihre Position wird durch einen Positionsvektor
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Dies erm glicht die Verallgemeinerung der Geschwindigkeit:
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
(ID 4354)
Die momentane ERROR:6029,0, bestimmt durch die Beziehung zwischen die Infinitesimal zurückgelegte Strecke ($ds$) und die Infinitesimale Variation of Time ($dt$), liefert eine genauere Sch tzung der tats chlichen Geschwindigkeit zu jedem Zeitpunkt von der Zeit ($t$), im Vergleich zu die Mittlere Geschwindigkeit ($\bar{v}$), die aus die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) mit der Gleichung berechnet wird:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Dies wird durch die Ableitung der Position nach der Zeit erreicht, d.h.:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Daher ist die momentane Geschwindigkeit die Geschwindigkeit ($v$) von die Position ($s$) zu jedem Zeitpunkt von der Zeit ($t$) mit gr erer Genauigkeit bekannt.
(ID 3153)
F r den Fall einer konstanten Geschwindigkeit ohne Anfangszeit kann die Position mit berechnet werden:
| $ s_v = s_0 + v_0 t $ |
Das entspricht einer Geraden mit:
• Steigung gleich der Geschwindigkeit $v_0$
• Anfangsposition $x_0$
wie unten dargestellt:

(ID 2244)
F r den Fall einer konstanten Geschwindigkeit und eines Anfangszeitpunkts kann die Position mit den Werten die Position ($s$), die Ausgangsstellung ($s_0$), die Konstante Geschwindigkeit ($v_0$), der Zeit ($t$) und der Startzeit ($t_0$) mithilfe der folgenden Gleichung berechnet werden:
| $ s = s_0 + v_0 ( t - t_0 )$ |
Die Gleichung entspricht einer geraden Linie mit:
• einer Steigung von die Konstante Geschwindigkeit ($v_0$)
• einem y-Achsenabschnitt bei die Ausgangsstellung ($s_0$) f r der Startzeit ($t_0$)
wie unten dargestellt:

(ID 2243)
Wenn sich ein K rper im "Ruhezustand" befindet, bedeutet dies, dass er im Ruhezustand bez glich unseres Bezugssystems oder Koordinatensystems ist. Dieser "Ruhezustand" ist jedoch v llig relativ, das hei t, von einem K rper aus, der sich relativ zu unserem System bewegt, ist der "ruhende" K rper auch in Bewegung.
In diesem Sinne gibt es keinen "absoluten Ruhezustand", sondern nur einen relativ zum jeweiligen Bezugssystem. Deshalb ist im Allgemeinen jede Geschwindigkeitsmessung eine Messung im Verh ltnis zu einem bestimmten Bezugssystem.
Wenn sich ein K rper zum Beispiel sehr langsam zu bewegen scheint, bedeutet dies nur, dass seine Geschwindigkeit der Geschwindigkeit des Bezugssystems, in dem die langsame Bewegung beobachtet wird, sehr hnlich ist.
(ID 4405)
Wenn die Geschwindigkeit konstant ist, wird die Geschwindigkeit gleich die Anfangsgeschwindigkeit ($v_0$) sein. In diesem Fall kann der zur ckgelegte Weg in Abh ngigkeit von der Zeit berechnet werden, indem die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) durch die Differenz zwischen der Zeit ($t$) und der Startzeit ($t_0$) geteilt wird:
| $ s = s_0 + v_0 ( t - t_0 )$ |
Die entsprechende Gleichung definiert eine gerade Linie im Raum-Zeit-Kontinuum.
(ID 3154)
Wenn wir ein Zeit ($t$) mit eine Position ($s$) ($s(t)$) nehmen und einen Punkt zu einer zuk nftigen Zeit $t+\Delta t$ mit einer Position $s(t+\Delta t)$ betrachten, k nnen wir die Geschwindigkeit als die Strecke im Zeitintervall $\Delta t$ absch tzen:
$s(t+\Delta t)-s(t)$
die Geschwindigkeit ($v$) kann berechnet werden, indem man die zur ckgelegte Strecke durch die vergangene Zeit teilt:
$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$
Wenn der Wert von $\Delta t$ kleiner wird, n hert sich die berechnete Geschwindigkeit der Tangente an die Positionscurve zur Zeit:

Dies verallgemeinert das, was bereits f r den Fall konstanter Geschwindigkeit gesehen wurde.
(ID 1638)
Wenn die Verschiebung als eine Linie zwischen dem Ursprung O und dem Punkt A dargestellt wird:

Sieht man, dass eine Strecke in einer bestimmten Zeit zur ckgelegt wurde. Daher entspricht die Steigung der Grafik Strecke vs. Zeit der Geschwindigkeit.
Wenn die Steigung gr er ist, bedeutet dies, dass eine Strecke in k rzerer Zeit zur ckgelegt wird, was einer h heren Geschwindigkeit entspricht.
Wenn die Steigung kleiner ist, bedeutet dies, dass eine Strecke in l ngerer Zeit zur ckgelegt wird, was einer niedrigeren Geschwindigkeit entspricht.
(ID 2239)
Im Fall eines Graphen mit einem Abschnitt negativer Steigung:

Liegt eine Situation vor, in der man von der Position B zur Position C zur ckgekehrt ist, die sich in einer Entfernung von Null befindet. Mit anderen Worten, negative Steigungen bedeuten, dass man sich in die entgegengesetzte Richtung bewegt, nicht weg vom Ursprung, sondern auf ihn zu.
(ID 2245)
Das Integral von die Geschwindigkeit ($v$) entspricht dem Bereich unter der Kurve, die diese Funktion definiert. Daher entspricht das Integral der Geschwindigkeit zwischen der Startzeit ($t_0$) und der Zeit ($t$) der zur ckgelegten Strecke zwischen die Ausgangsstellung ($s_0$) und die Position ($s$).
Deshalb haben wir:
| $ s = s_0 +\displaystyle\int_{t_0}^t v d\tau$ |
Was in der folgenden Grafik dargestellt ist:

Ich gehe als Bereich unter der Geschwindigkeits- und Zeitkurve.
(ID 2242)
Ein zweiter Fall sind horizontale Abschnitte im Weg-Zeit-Diagramm:

Wenn wir uns den Abschnitt AB ansehen, werden wir feststellen, dass sich der Weg trotz verstrichener Zeit nicht ver ndert hat. Das bedeutet, dass das Objekt angehalten ist. Daher entsprechen horizontale Abschnitte, die einer Nullsteigung entsprechen, Phasen, in denen die Geschwindigkeit null ist.
(ID 2241)
Die Geschwindigkeit eines Objekts in einem System mit mehr als einer Dimension wird traditionell durch einen Vektor definiert. Dieser Vektor hat seinen Ursprung am Objekt und ist in Richtung der Bewegung des Objekts orientiert.

(ID 2240)
ID:(35, 0)
