Position, mehr Dimensionen
Storyboard 
Um die Position eines Objekts in mehr als einer Dimension zu beschreiben, ist es notwendig, ein mehrdimensionales Koordinatensystem einzuführen. Dieses System zeichnet sich dadurch aus, dass jedem Punkt im Raum eine eindeutige Parameterkombination zugeordnet wird. Die Anzahl dieser Parameter entspricht der Anzahl der Dimensionen.
Die Wahl des Koordinatensystems kann vom zu modellierenden Problem abhängen. Einerseits strebt man an, die möglichst geringe Anzahl von Dimensionen zu haben, und andererseits sicherzustellen, dass die Beschreibung der Bewegung in jeder Dimension möglichst unabhängig von den anderen Dimensionen ist. Dies erleichtert die Lösung, da jede Dimension separat untersucht werden kann.
ID:(1201, 0)
Dimensionen
Definition 
Dimensionen sind die Parameter, die benötigt werden, um die Position eines Systems in einem bestimmten Raum zu beschreiben. Diese Parameter können Distanz, Länge, Breite und Höhe umfassen, um nur einige zu nennen. Dies ermöglicht es einem System, sich in einem bestimmten Raum zu befinden. Beispielsweise benötigt ein Fahrzeug auf einer Straße nur einen Parameter, um seinen Standort anzugeben, während ein Boot auf dem Ozean zwei Parameter und ein Flugzeug drei benötigt.
ID:(479, 0)
Darstellung der Position in zwei Dimensionen
Bild 
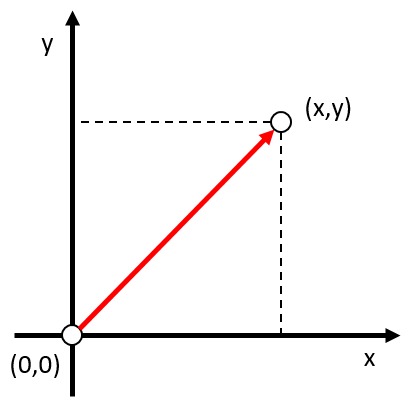
In einem zweidimensionalen System kann die Position eines Objekts durch einen Vektor dargestellt werden, der die Entfernung vom Ursprung von Null (Koordinaten $(0,0)$) in die Richtung angibt, in der sich das Objekt befindet. Beide Koordinaten werden als positive oder negative Menge gemessen, abhängig davon, ob sich das Objekt in der positiven oder negativen Richtung des jeweiligen Achsens befindet. Diese Position kann zum Beispiel durch den Parameter $(x,y)$ dargestellt werden, wobei die Skalare $x$ und $y$ die Entfernung vom Ursprung des Objekts in jeder Achse angeben.
ID:(2234, 0)
Darstellung der Position in drei Dimensionen
Notiz 
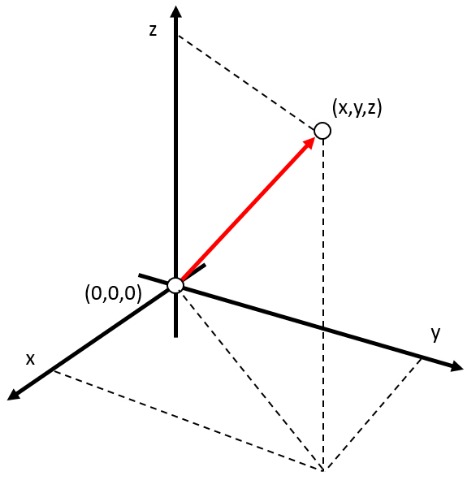
In einem zweidimensionalen System kann die Position eines Objekts durch einen Vektor dargestellt werden, der die Entfernung vom Ursprung von Null (Koordinaten $(0,0,0)$) in die Richtung angibt, in der sich das Objekt befindet. Beide Koordinaten werden als positive oder negative Menge gemessen, abhängig davon, ob sich das Objekt in der positiven oder negativen Richtung des jeweiligen Achsens befindet. Diese Position kann zum Beispiel durch den Parameter $(x,y,z)$ dargestellt werden, wobei die Skalare $x$, $y$ und $z$ die Entfernung vom Ursprung des Objekts in jeder Achse angeben.
ID:(2235, 0)
Tachometer
Zitat 
Ein Tachometer ist ein Gerät, das zur Messung der von einem Fahrzeug zurückgelegten Entfernung verwendet wird. Er befindet sich normalerweise auf dem Armaturenbrett oder Instrumentenpanel eines Autos und kann verwendet werden, um die insgesamt zurückgelegte Entfernung zu verfolgen. Ein Tachometer zählt die Umdrehungen einer Antriebswelle, die mit den Rädern des Fahrzeugs verbunden ist. Wenn das Fahrzeug sich bewegt, dreht sich die Antriebswelle, und jede Umdrehung der Antriebswelle wird gezählt und auf dem Tachometer aufgezeichnet. Der Tachometer ist in der Regel so kalibriert, dass er Entfernungen, die in Meilen oder Kilometern zurückgelegt wurden, genau messen kann.

ID:(480, 0)
Laser-Entfernungsmesser
Übung 
Ein Laserentfernungsmesser ist ein Gerät, das einen Laserstrahl verwendet, um die Entfernung zwischen zwei Punkten zu messen. Es funktioniert, indem es einen Laserimpuls sendet, der von dem zu messenden Objekt reflektiert und dann vom Entfernungsmesser detektiert wird. Die Zeit, die der Laserimpuls benötigt, um von dem Entfernungsmesser zum Objekt und zurück zu reisen, kann dann verwendet werden, um die Entfernung zwischen den beiden Punkten zu berechnen. Laserentfernungsmesser werden häufig in Vermessungen, Navigation und anderen Anwendungen eingesetzt, in denen präzise Messungen erforderlich sind.

ID:(481, 0)
GPS (Global Positioning System)
Gleichung 
Das Global Positioning System (GPS) ist ein satellitengestütztes Navigationssystem, das ein Netzwerk von 24 Satelliten verwendet, die die Erde umkreisen, um die exakte Position einer Person oder eines Objekts auf dem Planeten zu bestimmen. GPS-Empfänger berechnen die Entfernung zu jedem Satelliten, indem sie die Zeit messen, die die Signale benötigen, um vom Satelliten zum Empfänger zu gelangen. Sobald diese Entfernungen bekannt sind, kann der Empfänger einen Prozess namens Trilateration verwenden, um seine exakte Position, einschließlich Längen- und Breitengrad sowie Höhe, zu berechnen. Dies kann verwendet werden, um die Entfernungen zwischen zwei Standorten zu messen, sowie die Länge einer von einer Person oder einem Objekt zurückgelegten Strecke.

ID:(474, 0)
Zurückgelegte Strecke
Script 
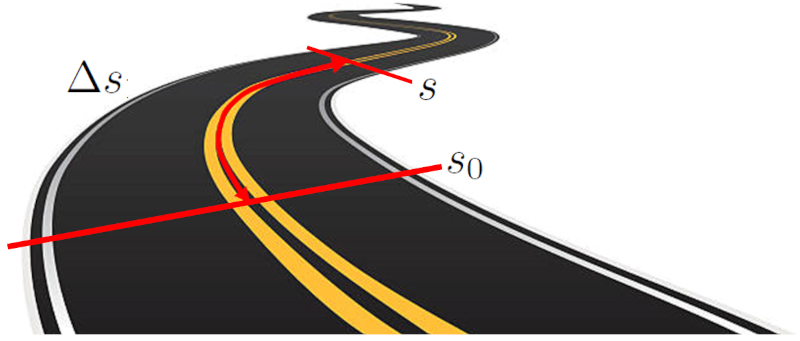
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) eines Objekts wird gemessen, indem man die Entfernung zwischen zwei spezifischen Punkten entlang einer Trajektorie misst. Diese Trajektorie kann eine Gerade auf einem kartesischen Koordinatensystem oder ein gekrümmter Pfad sein. Die Entfernung wird berechnet, indem man die Länge der Trajektorie zwischen den beiden Start- und Endpunkten misst.
ID:(9495, 0)
Ausgangsposition in mehr Dimensionen
Variable 
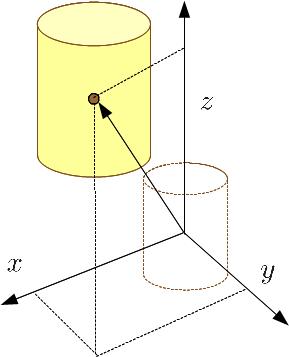
Die Anfangsposition eines Objekts ist sein Ort, bevor es sich bewegt. Diese Position kann in mehr als einer Dimension durch einen Vektor definiert werden, der vom Ursprung des Koordinatensystems zum Objekt geht und die gleiche Anzahl von Komponenten hat wie die vorhandenen Dimensionen.
ID:(2236, 0)
Zurückgelegte Distanz in mehr Dimensionen
Audio 
Um die Bewegung eines Objekts zu beschreiben, berechnen wir die Differenz zwischen einem Startpunkt und einem Endpunkt. Diese Differenz, genannt Entfernung, entspricht jedoch nicht immer der tatsächlichen Strecke, die das Objekt zurückgelegt hat, wenn der Weg gekrümmt ist. Die Krümmung des Weges führt dazu, dass die zurückgelegte Strecke größer ist als die Entfernung zwischen den beiden Punkten. Wenn die beiden Punkte sehr nah beieinander liegen, ist die Krümmung vernachlässigbar und die zurückgelegte Strecke entspricht der Entfernung zwischen den beiden Punkten.
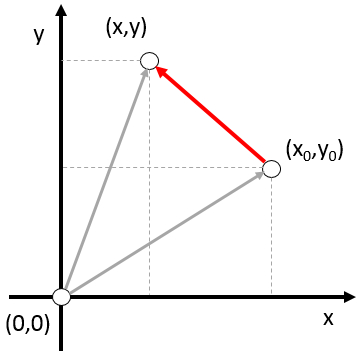
In diesem Fall sprechen wir von einer infinitesimalen Entfernung.
ID:(9496, 0)
Position, mehr Dimensionen
Beschreibung 
Um die Position eines Objekts in mehr als einer Dimension zu beschreiben, ist es notwendig, ein mehrdimensionales Koordinatensystem einzuführen. Dieses System zeichnet sich dadurch aus, dass jedem Punkt im Raum eine eindeutige Parameterkombination zugeordnet wird. Die Anzahl dieser Parameter entspricht der Anzahl der Dimensionen. Die Wahl des Koordinatensystems kann vom zu modellierenden Problem abhängen. Einerseits strebt man an, die möglichst geringe Anzahl von Dimensionen zu haben, und andererseits sicherzustellen, dass die Beschreibung der Bewegung in jeder Dimension möglichst unabhängig von den anderen Dimensionen ist. Dies erleichtert die Lösung, da jede Dimension separat untersucht werden kann.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Dimensionen sind die Parameter, die ben tigt werden, um die Position eines Systems in einem bestimmten Raum zu beschreiben. Diese Parameter k nnen Distanz, L nge, Breite und H he umfassen, um nur einige zu nennen. Dies erm glicht es einem System, sich in einem bestimmten Raum zu befinden. Beispielsweise ben tigt ein Fahrzeug auf einer Stra e nur einen Parameter, um seinen Standort anzugeben, w hrend ein Boot auf dem Ozean zwei Parameter und ein Flugzeug drei ben tigt.
(ID 479)
In einem zweidimensionalen System kann die Position eines Objekts durch einen Vektor dargestellt werden, der die Entfernung vom Ursprung von Null (Koordinaten $(0,0)$) in die Richtung angibt, in der sich das Objekt befindet. Beide Koordinaten werden als positive oder negative Menge gemessen, abh ngig davon, ob sich das Objekt in der positiven oder negativen Richtung des jeweiligen Achsens befindet. Diese Position kann zum Beispiel durch den Parameter $(x,y)$ dargestellt werden, wobei die Skalare $x$ und $y$ die Entfernung vom Ursprung des Objekts in jeder Achse angeben.

(ID 2234)
In einem zweidimensionalen System kann die Position eines Objekts durch einen Vektor dargestellt werden, der die Entfernung vom Ursprung von Null (Koordinaten $(0,0,0)$) in die Richtung angibt, in der sich das Objekt befindet. Beide Koordinaten werden als positive oder negative Menge gemessen, abh ngig davon, ob sich das Objekt in der positiven oder negativen Richtung des jeweiligen Achsens befindet. Diese Position kann zum Beispiel durch den Parameter $(x,y,z)$ dargestellt werden, wobei die Skalare $x$, $y$ und $z$ die Entfernung vom Ursprung des Objekts in jeder Achse angeben.

(ID 2235)
Ein Tachometer ist ein Ger t, das zur Messung der von einem Fahrzeug zur ckgelegten Entfernung verwendet wird. Er befindet sich normalerweise auf dem Armaturenbrett oder Instrumentenpanel eines Autos und kann verwendet werden, um die insgesamt zur ckgelegte Entfernung zu verfolgen. Ein Tachometer z hlt die Umdrehungen einer Antriebswelle, die mit den R dern des Fahrzeugs verbunden ist. Wenn das Fahrzeug sich bewegt, dreht sich die Antriebswelle, und jede Umdrehung der Antriebswelle wird gez hlt und auf dem Tachometer aufgezeichnet. Der Tachometer ist in der Regel so kalibriert, dass er Entfernungen, die in Meilen oder Kilometern zur ckgelegt wurden, genau messen kann.

(ID 480)
Ein Laserentfernungsmesser ist ein Ger t, das einen Laserstrahl verwendet, um die Entfernung zwischen zwei Punkten zu messen. Es funktioniert, indem es einen Laserimpuls sendet, der von dem zu messenden Objekt reflektiert und dann vom Entfernungsmesser detektiert wird. Die Zeit, die der Laserimpuls ben tigt, um von dem Entfernungsmesser zum Objekt und zur ck zu reisen, kann dann verwendet werden, um die Entfernung zwischen den beiden Punkten zu berechnen. Laserentfernungsmesser werden h ufig in Vermessungen, Navigation und anderen Anwendungen eingesetzt, in denen pr zise Messungen erforderlich sind.

(ID 481)
Das Global Positioning System (GPS) ist ein satellitengest tztes Navigationssystem, das ein Netzwerk von 24 Satelliten verwendet, die die Erde umkreisen, um die exakte Position einer Person oder eines Objekts auf dem Planeten zu bestimmen. GPS-Empf nger berechnen die Entfernung zu jedem Satelliten, indem sie die Zeit messen, die die Signale ben tigen, um vom Satelliten zum Empf nger zu gelangen. Sobald diese Entfernungen bekannt sind, kann der Empf nger einen Prozess namens Trilateration verwenden, um seine exakte Position, einschlie lich L ngen- und Breitengrad sowie H he, zu berechnen. Dies kann verwendet werden, um die Entfernungen zwischen zwei Standorten zu messen, sowie die L nge einer von einer Person oder einem Objekt zur ckgelegten Strecke.

(ID 474)
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) wird f r ein Objekt bestimmt, indem die Entfernung zwischen zwei bestimmten Punkten entlang eines Pfads gemessen wird. Dieser Pfad kann eine gerade Linie in einem kartesischen Koordinatensystem oder eine gekr mmte Bahn sein. Die Entfernung wird als die L nge des Pfads berechnet, der die Anfangs- und Endpunkte verbindet.

Zur ckgelegte Strecke von einem Anfangspunkt zu einem Endpunkt
Da der Wert von die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) berechnet wird:
| $ \Delta s = s_2 - s_1 $ |
ist es m glich, den Ursprung der Position zu verschieben, indem ein konstanter Wert $d$ zu beiden Gr en addiert wird:
$s \rightarrow s + d$
$s_0 \rightarrow s_0 + d$
ohne das Ergebnis der zur ckgelegten Strecke zu beeinflussen:
$\Delta s = s - s_0 \rightarrow (s + d) - (s_0 + d) = s - s_0 = \Delta s$
Dieses Konzept wird als r umliche Invarianz bezeichnet, was bedeutet, dass der Wert der zur ckgelegten Strecke nicht davon abh ngt, wo genau die Messung beginnt.
Das bedeutet, dass die mit diesem Prinzip formulierten Gesetze r umlich invariant sind, das hei t, sie gelten unabh ngig davon, wo die Messung durchgef hrt wird.
(ID 9495)
Um die Bewegung eines Objekts zu beschreiben, ist es notwendig, die zur ckgelegte Strecke zu berechnen. Dazu werden die Anfangs- und Endpunkte des Objekts mithilfe von Vektoren definiert, und die Entfernung wird berechnet, indem ein Vektor vom anderen subtrahiert wird. Dies entspricht nur dem zur ckgelegten Weg, wenn die Verschiebung geradlinig ist, was in der Regel der Fall ist, wenn beide Punkte sehr nah beieinander liegen, wie im Fall von die Entfernung Run ($\Delta\vec{s}$), wobei die Position von Ursprung ($\vec{s}_0$) von die Aktuelle Position ($\vec{s}$) subtrahiert wird:
| $ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
(ID 714)
Die Anfangsposition eines Objekts ist sein Ort, bevor es sich bewegt. Diese Position kann in mehr als einer Dimension durch einen Vektor definiert werden, der vom Ursprung des Koordinatensystems zum Objekt geht und die gleiche Anzahl von Komponenten hat wie die vorhandenen Dimensionen.

(ID 2236)
Um die Bewegung eines Objekts zu beschreiben, berechnen wir die Differenz zwischen einem Startpunkt und einem Endpunkt. Diese Differenz, genannt Entfernung, entspricht jedoch nicht immer der tats chlichen Strecke, die das Objekt zur ckgelegt hat, wenn der Weg gekr mmt ist. Die Kr mmung des Weges f hrt dazu, dass die zur ckgelegte Strecke gr er ist als die Entfernung zwischen den beiden Punkten. Wenn die beiden Punkte sehr nah beieinander liegen, ist die Kr mmung vernachl ssigbar und die zur ckgelegte Strecke entspricht der Entfernung zwischen den beiden Punkten.

In diesem Fall sprechen wir von einer infinitesimalen Entfernung.
(ID 9496)
Im Falle eines Raums mit mehr als einer Dimension muss der Weg zwischen zwei Punkten nicht zwangsl ufig gerade verlaufen, wie es in eindimensionalen R umen der Fall ist. In solchen Situationen wird ein Vektor, der die Entfernung zwischen zwei Punkten entlang des Weges darstellt, immer gleich oder kleiner als die tats chliche Entfernung entlang des Weges sein. Wenn jedoch der Abstand zwischen den beiden Punkten infinitesimal oder sehr klein ist, werden beide bereinstimmen. Daher ist es n tzlich, den infinitesimalen Vektor zu definieren, der es uns erm glicht, das Verhalten eines Objekts in einem kontinuierlichen Raum pr zise zu beschreiben.
Daher wird der Wegelement zurückgelegt ($d\vec{s}$) als die Differenz zwischen die Aktuelle Position ($\vec{s}$) und die Position von Ursprung ($\vec{s}_0$) eingef hrt als:
| $d\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
(ID 9497)
ID:(1201, 0)
