Schwerkraft Axis nach unten
Notiz 
Wenn ein Koordinatensystem verwendet wird, bei dem die positive z-Achse nach oben zeigt, entspricht die Gravitation einem Beschleunigungsprozess in Richtung nach unten:
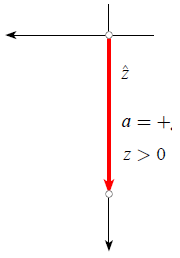
Schwerkraft mit nach unten weisender Achse
ID:(2249, 0)
Schwerkraft Axis nach oben
Zitat 
Wenn ein Koordinatensystem verwendet wird, bei dem die negative z-Achse nach unten zeigt, entspricht die Gravitation einem Beschleunigungsprozess in dieselbe Richtung wie die z-Achse:
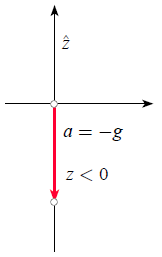
Schwerkraft mit nach oben zeigender Achse
ID:(2250, 0)
Meschlicher Körper Modell
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
Da ein Vektor als eine Anordnung seiner verschiedenen Komponenten ausgedr ckt werden kann,
$\vec{v}=(v_x,v_y,v_z)$
kann seine Ableitung als Ableitung jeder seiner Komponenten ausgedr ckt werden:
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
Im Allgemeinen gilt, dass die instantane Geschwindigkeit in mehr als einer Dimension
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
(ID 3155)
Im Falle, dass die konstante Beschleunigung ($a_0$) gleich die Mittlere Beschleunigung ($\bar{a}$) ist, wird es gleich
| $ a_0 = \bar{a} $ |
.
Deshalb, wenn wir die Geschwindigkeit Unterschied ($\Delta v$) als
| $ dv \equiv v - v_0 $ |
und der Abgelaufene Zeit ($\Delta t$) als
| $ \Delta t \equiv t - t_0 $ |
betrachten, kann die Gleichung f r die konstante Beschleunigung ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
als
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
geschrieben werden, und durch Umstellen erhalten wir
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
Im Fall von die konstante Beschleunigung ($a_0$) ist die Geschwindigkeit ($v$) als Funktion von der Zeit ($t$) eine Gerade, die durch der Startzeit ($t_0$) und die Anfangsgeschwindigkeit ($v_0$) verl uft und durch die Gleichung definiert ist:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Da die Zurückgelegte Strecke in einer Zeit ($\Delta s$) den Bereich unter der Geschwindigkeits-Zeit-Kurve darstellt, k nnen wir die Beitr ge des Rechtecks summieren:
$v_0(t-t_0)$
und des Dreiecks:
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Um die Zurückgelegte Strecke in einer Zeit ($\Delta s$) mit die Position ($s$) und die Ausgangsstellung ($s_0$) zu erhalten, ergibt sich:
| $ \Delta s = s - s_0 $ |
Daraus folgt:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Wenn wir die Gleichungen f r der Zeit ($t$) und der Startzeit ($t_0$) in die Gleichung f r die Geschwindigkeit ($v$) aufl sen, die von die Anfangsgeschwindigkeit ($v_0$) und die konstante Beschleunigung ($a_0$) abh ngt:
| $ v = v_0 + a_0 ( t - t_0 )$ |
erhalten wir:
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Dann, wenn wir diesen Ausdruck in die Gleichung f r die Position ($s$) mit die Ausgangsstellung ($s_0$) einsetzen:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
erhalten wir einen Ausdruck f r den zur ckgelegten Weg in Abh ngigkeit von der Geschwindigkeit:
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
Die Definition von die Mittlere Beschleunigung ($\bar{a}$) wird als die Beziehung zwischen die Geschwindigkeit Unterschied ($\Delta v$) und der Abgelaufene Zeit ($\Delta t$) betrachtet. Das hei t,
| $ dv \equiv v - v_0 $ |
und
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Kreiselbeschleunigung ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
innerhalb dieses Zeitintervalls definiert.
(ID 3678)
(ID 4355)
Wenn wir die Differenz von die Geschwindigkeit ($v$) zu den Zeiten $t+\Delta t$ und $t$ betrachten:
$\Delta v = v(t+\Delta t)-v(t)$
und $\Delta t$ als der Abgelaufene Zeit ($\Delta t$) nehmen, dann im Grenzwert von infinitesimal kurzen Zeiten:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Diese letzte Ausdruck entspricht der Ableitung der Funktion die Geschwindigkeit ($v$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
welche wiederum die Steigung der grafischen Darstellung dieser Funktion bei der Zeit ($t$) ist.
(ID 4356)
En el caso de que se asuma que el tiempo inicial es nulo\\n\\n
$t_0=0$
la ecuaci n de la posici n
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
se reduce a
| $ s = s_0 + v_0 t +\displaystyle\frac{1}{2} a_0 t ^2$ |
(ID 4360)
Beispiele
(ID 2247)
(ID 2246)
Wenn ein Koordinatensystem verwendet wird, bei dem die positive z-Achse nach oben zeigt, entspricht die Gravitation einem Beschleunigungsprozess in Richtung nach unten:
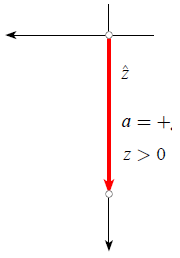
Schwerkraft mit nach unten weisender Achse
(ID 2249)
Wenn ein Koordinatensystem verwendet wird, bei dem die negative z-Achse nach unten zeigt, entspricht die Gravitation einem Beschleunigungsprozess in dieselbe Richtung wie die z-Achse:

Schwerkraft mit nach oben zeigender Achse
(ID 2250)
Im Fall einer zweistufigen Bewegung kann die erste Stufe durch eine Funktion beschrieben werden, die die Punkte der Startzeit ($t_0$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$), die Anfangsgeschwindigkeit ($v_0$) und die Geschwindigkeit der ersten Stufe ($v_1$) einbezieht und durch eine Gerade mit einer Steigung von die Beschleunigung während der ersten Stufe ($a_1$) dargestellt wird:
| $ v = v_0 + a_0 ( t - t_0 )$ |
F r die zweite Stufe, definiert durch die Punkte die Geschwindigkeit der ersten Stufe ($v_1$), die Geschwindigkeit der zweiten Stufe ($v_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$), wird eine zweite Gerade mit einer Steigung von die Beschleunigung während der zweiten Stufe ($a_2$) verwendet:
| $ v = v_0 + a_0 ( t - t_0 )$ |
die wie folgt dargestellt wird:
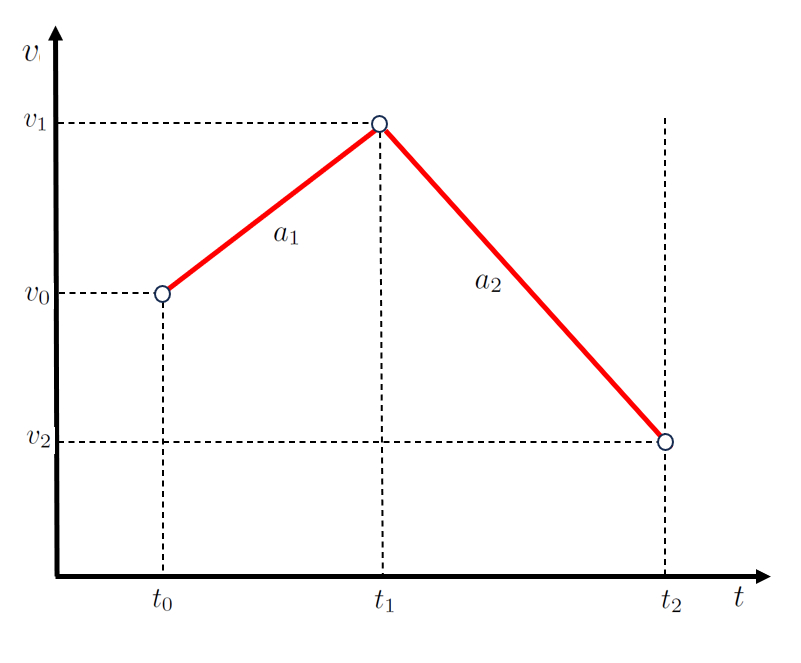
(ID 4357)
Es wird gesagt, dass Galileo seine Experimente durchgef hrt hat, um die Schwerkraft zu untersuchen, indem er Gegenst nde vom Turm von Pisa fallen lie :

Turm von Pisa
(ID 2248)
Wenn man beobachtet, dass die Geschwindigkeit ($v$) gleich die Zurückgelegte Strecke in einer Zeit ($\Delta s$) pro der Abgelaufene Zeit ($\Delta t$) ist, deutet dies darauf hin, dass der Weg gegeben ist durch:
$\Delta s = v\Delta t$
Da das Produkt $v\Delta t$ die Fl che unter der Geschwindigkeits-zu-Zeit-Kurve repr sentiert, was auch gleich dem zur ckgelegten Weg ist:
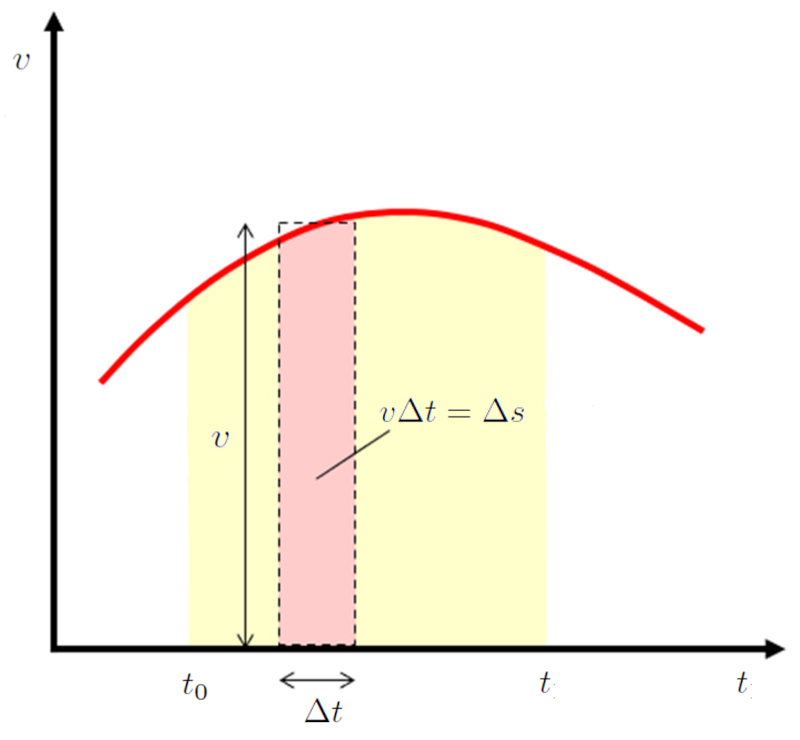
Diese Fl che kann auch mit dem Integral der entsprechenden Funktion berechnet werden. Daher entspricht das Integral der Beschleunigung zwischen der Startzeit ($t_0$) und der Zeit ($t$) der nderung der Geschwindigkeit zwischen der Anfangsgeschwindigkeit die Anfangsgeschwindigkeit ($v_0$) und die Geschwindigkeit ($v$):
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
(ID 2252)
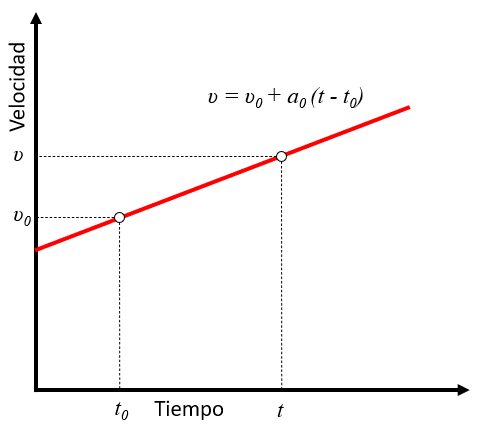
Wenn die Beschleunigung konstant ist, ndert sich die Geschwindigkeits nderung, die durch die Geschwindigkeit ($v$) dargestellt wird, linear in Abh ngigkeit von der Zeit ($t$). Dies kann mithilfe von die Anfangsgeschwindigkeit ($v_0$), die konstante Beschleunigung ($a_0$) und der Startzeit ($t_0$) berechnet werden und ergibt die Gleichung:
| $ v = v_0 + a_0 ( t - t_0 )$ |
Diese Beziehung wird grafisch als eine gerade Linie dargestellt, wie unten gezeigt:
(ID 2253)
Im Fall einer zweistufigen Bewegung f llt die Position, an der die erste Stufe endet, mit der Position zusammen, an der die zweite Stufe beginnt ($s_1$).
Ebenso f llt die Zeit, zu der die erste Stufe endet, mit der Zeit zusammen, zu der die zweite Stufe beginnt ($t_1$).
Da die Bewegung durch die erfahrene Beschleunigung definiert ist, muss die Geschwindigkeit, die am Ende der ersten Stufe erreicht wird, mit der Anfangsgeschwindigkeit der zweiten Stufe bereinstimmen ($v_1$).
Im Fall einer konstanten Beschleunigung h ngt in der ersten Stufe der Erste Endposition und begonnene zweite Etappe ($s_1$) von die Ausgangsstellung ($s_0$), die Anfangsgeschwindigkeit ($v_0$), die Beschleunigung während der ersten Stufe ($a_1$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Startzeit ($t_0$) ab, wie folgt:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
In der zweiten Stufe h ngt die Endposition der zweiten Etappe ($s_2$) von der Erste Endposition und begonnene zweite Etappe ($s_1$), die Geschwindigkeit der ersten Stufe ($v_1$), die Beschleunigung während der zweiten Stufe ($a_2$), der Endzeit der ersten und Beginn der zweiten Etappe ($t_1$) und der Endzeit der zweiten Etappe ($t_2$) ab, wie folgt:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
was wie folgt dargestellt wird:
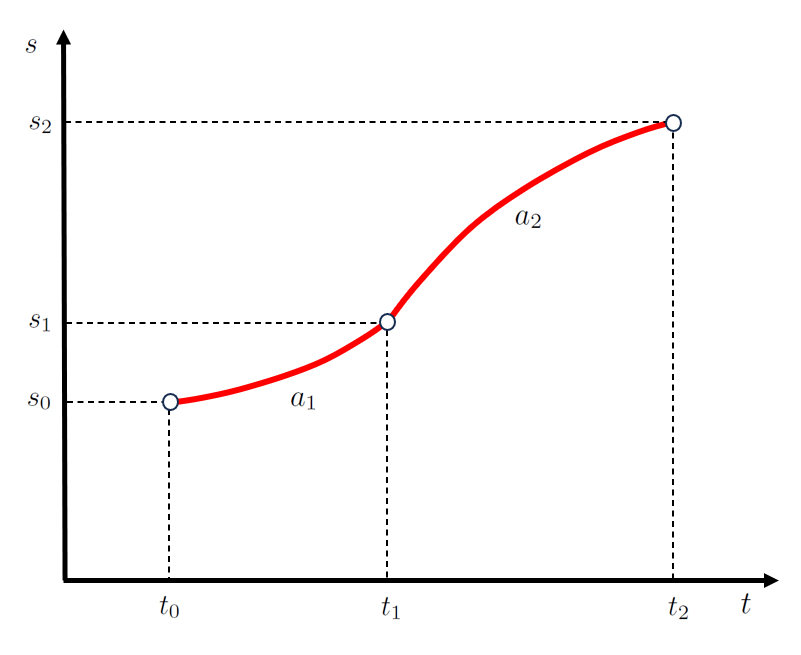
Fl che unter der konstanten Beschleunigungskurve
(ID 2254)
Wenn wir einen Bereich mit der Breite $\Delta t$ auf einem Geschwindigkeits-Zeit-Diagramm betrachten, entspricht dies dem zur ckgelegten Weg w hrend dieser Zeit:

Im speziellen Fall, in dem die Beschleunigung konstant ist, wird die Geschwindigkeit auf dem Geschwindigkeits-Zeit-Diagramm als eine gerade Linie dargestellt. Diese Linie wird durch die Geschwindigkeit ($v$), die Anfangsgeschwindigkeit ($v_0$), die konstante Beschleunigung ($a_0$), der Zeit ($t$) und der Startzeit ($t_0$) definiert, gleich:
| $ v = v_0 + a_0 ( t - t_0 )$ |
und wird wie folgt grafisch dargestellt:
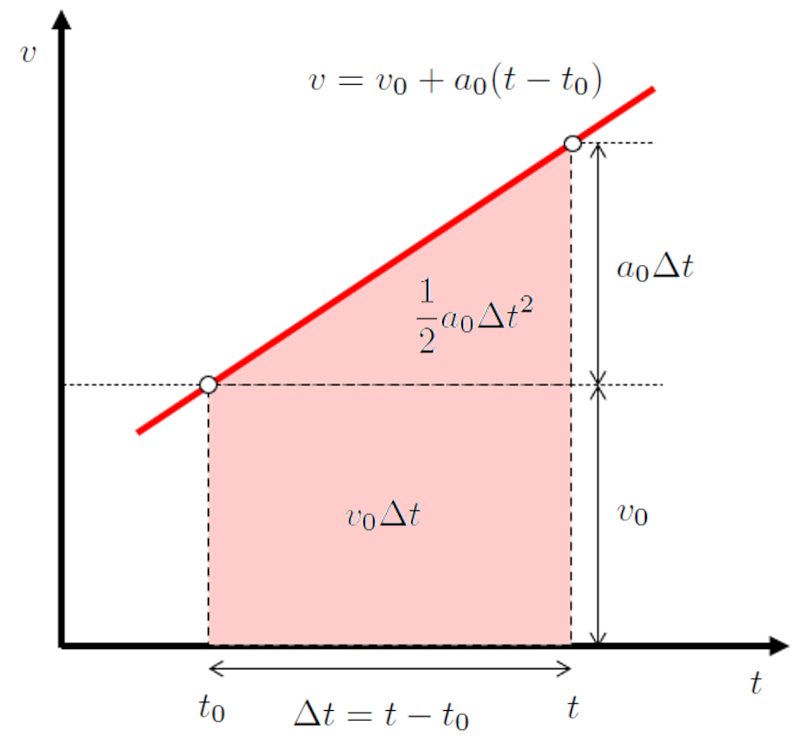
Da die Fl che unter der Kurve als Summe aus einem Rechteck mit der Fl che
$v_0(t-t_0)$
und einem Dreieck mit der Fl che
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
repr sentiert werden kann, k nnen wir den Weg die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Position ($s$) und die Ausgangsstellung ($s_0$) berechnen, was zu folgendem f hrt:
| $ \Delta s = s - s_0 $ |
Daher ist die Position ($s$) gleich:
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 4828)
In einem Szenario mit Bewegung in zwei Stufen ndert das Objekt zun chst seine Geschwindigkeit um die Geschwindigkeitsunterschied in der ersten Stufe ($\Delta v_1$) w hrend eines Zeitintervalls von ein In der ersten Phase verstrichene Zeit ($\Delta t_1$) mit einer Beschleunigung von eine Beschleunigung während der ersten Stufe ($a_1$).
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
Anschlie end, in der zweiten Stufe, bewegt es sich weiter und ndert seine Geschwindigkeit um die Geschwindigkeitsunterschied in der zweiten Stufe ($\Delta v_2$) w hrend eines Zeitintervalls von der In der zweiten Phase verbrachte Zeit ($\Delta t_2$) mit einer Beschleunigung von die Beschleunigung während der zweiten Stufe ($a_2$).
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
Wenn dies grafisch dargestellt wird, erhalten wir ein Diagramm von Geschwindigkeit und Zeit, wie unten dargestellt:
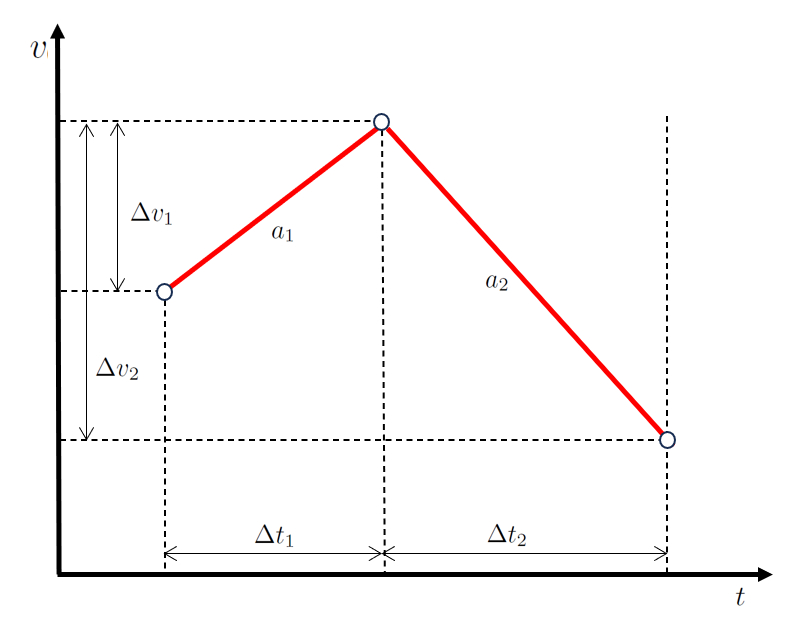
Der Schl ssel hier ist, dass die Werte der In der ersten Phase verstrichene Zeit ($\Delta t_1$) und der In der zweiten Phase verbrachte Zeit ($\Delta t_2$) sequenziell sind, genauso wie die Werte die Geschwindigkeitsunterschied in der ersten Stufe ($\Delta v_1$) und die Geschwindigkeitsunterschied in der zweiten Stufe ($\Delta v_2$).
(ID 4829)
ID:(36, 0)
