Druyd:Knowledge

Mathematischen Pendel

Storyboard

Bei einem Pendel aus einer Punktmasse ergibt sich die potentielle Energie aus der Erhöhung der Masse gegen das Gravitationsfeld, wenn das Pendel um einen bestimmten Winkel abweicht.

>Modell

ID:(1420, 0)

Mathematischen Pendel

Modell

Im Fall eines Pendels mit Punktmasse wird die potenzielle Energie durch das Anheben der Masse gegen das Gravitationsfeld erzeugt, wenn das Pendel um einen bestimmten Winkel ausgelenkt wird.

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$\theta_0$

theta_0

Anfangswinkel

rad

$\nu$

Frequenz des Schalls

$m_g$

m_g

Gravitationsmasse

$K$

Kinetische Energie der Punktmasse

$\omega_0$

omega_0

Kreisfrequenz Mathematische Pendel

rad/s

$L$

Pendel Länge

$V$

Potenzielle Energie Pendulum, für kleine Winkel

$\theta$

theta

Schwenkwinkel

rad

$E$

Totale Energie

$m_i$

m_i

Träge Masse

$\omega$

omega

Winkelgeschwindigkeit

rad/s

$T$

Zeit

$t$

Zeit

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$E = K + V$

E = K + V

(ID 3687)

$\nu =\displaystyle\frac{1}{ T }$

nu =1/ T

(ID 4427)

$V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

V = m_g * g * L * theta ^2/2

Die potenzielle Gravitationsenergie eines Pendels mit Masse m, das an einem Faden der L nge L aufgeh ngt ist und um einen Winkel \theta ausgelenkt wird, ist gegeben durch

$U = m g L (1-\cos \theta )$

wobei g die Erdbeschleunigung ist.

F r kleine Winkel kann die Kosinus-Funktion durch eine Taylor-Reihenentwicklung bis zur zweiten Ordnung approximiert werden

$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$

Diese N herung f hrt zu einer Vereinfachung der potenziellen Energie zu

$V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

(ID 4514)

$K =\displaystyle\frac{1}{2} m_i L ^2 \omega ^2$

K = m_i * L ^2* omega ^2/2

(ID 4515)

$\omega_0 ^2=\displaystyle\frac{ g }{ L }$

omega_0 ^2 = g / L

Die Kinetische Energie der Punktmasse ( $K$ ) in Bezug auf die Träge Masse ( $m_i$ ), der Pendel Länge ( $L$ ) und die Winkelgeschwindigkeit ( $\omega$ ) wird ausgedrückt durch:

$K =\displaystyle\frac{1}{2} m_i L ^2 \omega ^2$

Analog dazu wird die Potenzielle Energie Pendulum ( $V$ ) in Abhängigkeit von die Gravitationsbeschleunigung ( $g$ ) und die Gravitationsmasse ( $m_g$ ) beschrieben durch:

$V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

Unter Berücksichtigung von der Schwenkwinkel ( $\theta$ ) ergibt sich die Gleichung für die Gesamtenergie als:

$E = \displaystyle\frac{1}{2}m r^2 \omega^2 + \displaystyle\frac{1}{2}m g r \theta^2$

Da die Zeit ( $T$ ) gleich ist:

$T = 2\pi\displaystyle\sqrt{\displaystyle\frac{m r^2}{m g r}} = 2\pi\displaystyle\sqrt{\displaystyle\frac{r}{g}}$

Kann die Beziehung für die Kreisfrequenz Mathematische Pendel ( $\omega_0$ ) wie folgt aufgestellt werden:

$\omega_0 ^2=\displaystyle\frac{ g }{ L }$

(ID 4516)

$\omega = \displaystyle\frac{2 \pi }{ T }$

omega = 2* pi / T

(ID 12335)

$\omega = 2 \pi \nu$

omega = 2* pi * nu

(ID 12338)

$m_g = m_i$

m_g = m_i

(ID 12552)

$x = x_0 \cos \omega_0 t$

x = x_0 *cos( omega_0 * t )

(ID 14074)

$v = - x_0 \omega_0 \sin \omega_0 t$

v = - x_0 * omega_0 *sin( omega_0 * t )

Mit der komplexen Zahl

$z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t$

eingef hrt in

$\dot{z} = i \omega_0 z$

erhalten wir

$\dot{z} = i\omega_0 z = i \omega_0 x_0 \cos \omega_0 t - \omega_0 x_0 \sin \omega_0 t$

daher wird die Geschwindigkeit als der Realteil erhalten

$v = - x_0 \omega_0 \sin \omega_0 t$

(ID 14076)

Beispiele

Simulation des mathematischen Pendels

Eine wirkungsvolle Methode zur Untersuchung der Schwingung eines mathematischen Pendels ist die Darstellung seiner Bewegung im Phasenraum, der das System ber Impuls und Position beschreibt. In diesem Fall entspricht der Impuls dem Drehimpuls, w hrend die Position durch den Ablenkwinkel dargestellt wird:

(ID 15849)

Schwingungen mit einem mathematischen Pendel

Ein Pendel wird beschrieben als eine die Gravitationsmasse ( $m_g$ ), die an einer Schnur aufgehängt ist, die am Drehpunkt befestigt ist, in einem Abstand von der Pendel Länge ( $L$ ). Es wird als mathematisches Pendel bezeichnet, da es eine Idealisierung des physikalischen Pendels darstellt, bei der die Masse als Punktmasse betrachtet wird, also an einem einzigen Punkt konzentriert ist.

(ID 7098)

Mathematisches Pendel

Ein Pendel besteht aus die Gravitationsmasse ( $m_g$ ), das an einer Schnur aufgehängt ist, die am Drehpunkt von der Pendel Länge ( $L$ ) befestigt ist. Dieses Modell wird als mathematisches Pendel bezeichnet, da es eine Idealisierung des physikalischen Pendels darstellt, bei der die gesamte Masse in einem Punkt konzentriert ist.

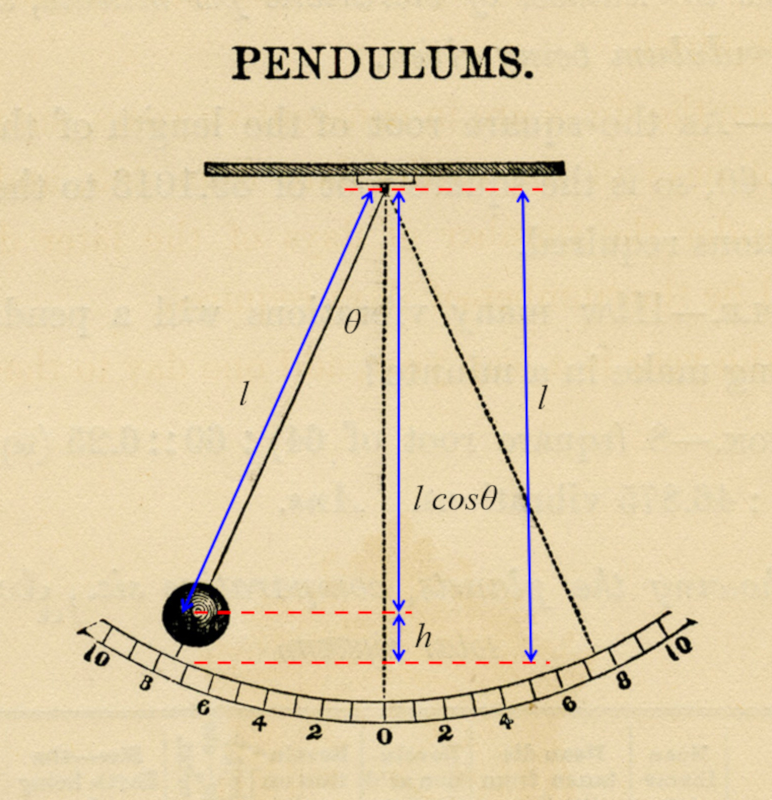
(ID 1180)

Modell

(ID 15852)

ID:(1420, 0)