User:
Thermal conduction
Storyboard 
Heat transport consists of two alternating processes. On one hand, there is conduction through a medium, and on the other, the transfer of heat from one medium to another.
Transport through a medium involves the transfer of heat into the medium, followed by conduction through it, and finally, the transmission of heat out of the medium. In more complex media, multiple stages of conduction and transfer between different media must be considered. If heat is generated or absorbed in one of the media, conduction from or to that heat source or sink is accounted for.
ID:(313, 0)
Heat conduction mechanism
Image
The heat conducted by a
and the conductivity
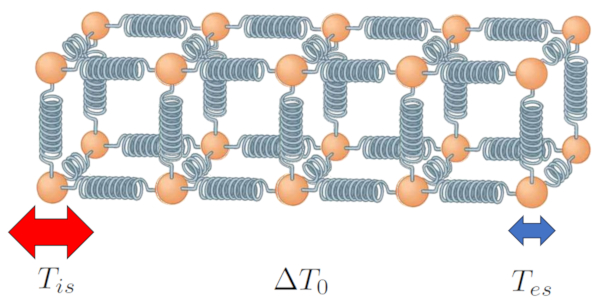
ID:(7718, 0)
Geometry and material dependence
Note
One of the key factors determining how much heat can be conducted through a solid or liquid is its cross-sectional area, which refers to the quantity of atom chains available. The more of these chains we have, the greater our heat transport capacity.
However, the length of these chains can be counterproductive. As the spring chain becomes longer, our ability to transmit heat decreases, as more atoms must adjust their oscillation amplitudes.
If we represent this with the section ($S$) and the conductor length ($L$), the diagram takes the following form:
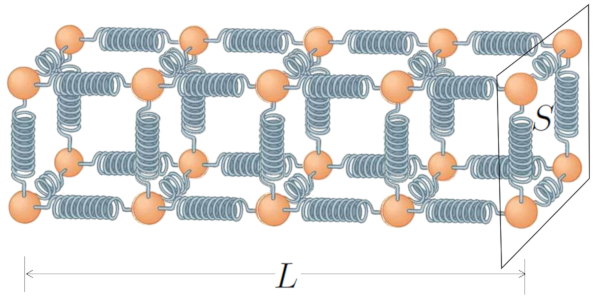
Finally, the ability of the medium and material to transport heat, described by coefficients the internal transmission coefficient ($\alpha_i$) and the external transmission coefficient ($\alpha_e$), and the thermal conductivity ($\lambda$), explains how heat moves in response to the temperature difference ($\Delta T$) created by the difference between the indoor temperature ($T_i$) and the outdoor temperature ($T_e$):
This is calculated as:
| $ \Delta T = T_i - T_e $ |
ID:(15235, 0)
Heat conduction
Quote
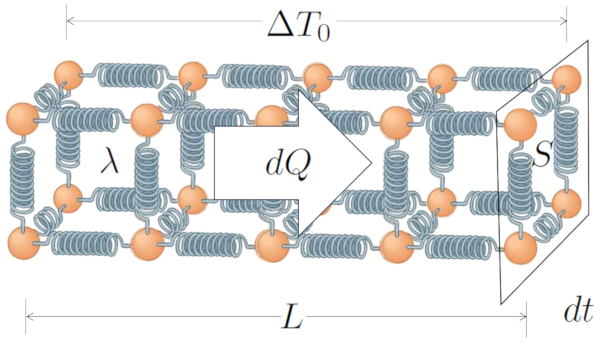
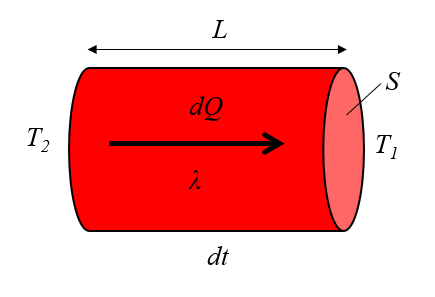
Heat conduction was first modeled by Jean Baptiste Joseph Fourier [1], who established that the heat flow rate ($q$), defined using the heat transported ($dQ$), the time variation ($dt$), and the section ($S$), is expressed by:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
This theory is also related to the section ($S$), the conductor length ($L$), the temperature difference in the conductor ($\Delta T_0$), and the thermal conductivity ($\lambda$), as shown in:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
and is illustrated with the following diagram:
[1] "Théorie Analytique de la Chaleur" (The Analytical Theory of Heat), Jean Baptiste Joseph Fourier, 1822.
ID:(15236, 0)
