Heat Transportation
Storyboard 
Heat transport through a system composed of multiple media can be estimated by analyzing how heat is conducted within each medium and transferred at each interface. The calculation is performed using the specific parameters of each medium and interface, as well as the temperatures at both ends of the system, thereby providing the temperatures at each interface.
ID:(1483, 0)
Heat transport
Image 
The basic system includes a transfer generated by the temperature difference ($\Delta T$), which consists of the temperature difference at internal interface ($\Delta T_i$), the temperature difference in the conductor ($\Delta T_0$), and the temperature difference at external interface ($\Delta T_e$). Therefore:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
With the heat flow rate ($q$) being responsible for the transfer between the interior and the conductor, using the internal transmission coefficient ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
Conduction involves the thermal conductivity ($\lambda$) and the conductor length ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
And the transfer from the conductor to the exterior, with the external transmission coefficient ($\alpha_e$), is represented by:
| $ q = \alpha_e \Delta T_e $ |
All this is graphically represented by:
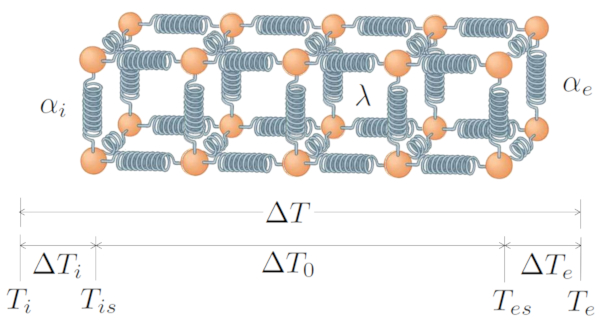
ID:(7723, 0)
Heat transport between two systems via a third medium
Note 
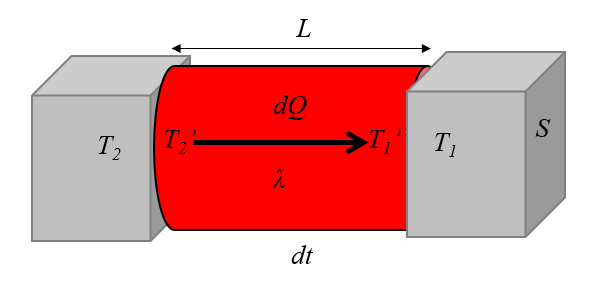
The heat flow rate ($q$) is calculated from the total transport coefficient (multiple medium, two interfaces) ($k$) and the temperature difference ($\Delta T$) using the following equation:
| $ q = k \Delta T $ |
where the total transport coefficient (multiple medium, two interfaces) ($k$) is derived from the external transmission coefficient ($\alpha_e$), the internal transmission coefficient ($\alpha_i$), the thermal conductivity ($\lambda$), and the conductor length ($L$) through this equation:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
This is represented in the image below:
ID:(1675, 0)
Temperature Profile
Quote 
Typically, the temperature variation within a conductor follows a linear pattern. However, in the case of gaseous and/or liquid media in contact with the conductor, there is a gradual temperature variation from the center of the medium to the surface, as depicted in the following image:
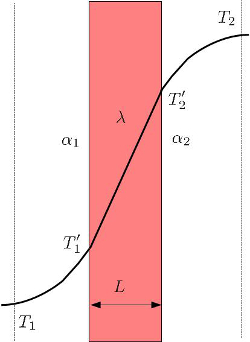
the outer surface temperature ($T_{es}$) depends on the outdoor Temperature ($T_e$), the coefficient of total transportation ($k$), the external transmission coefficient ($\alpha_e$), and the temperature difference ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
the inner surface temperature ($T_{is}$) is a function of the indoor temperature ($T_i$) and the internal transmission coefficient ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
and the temperature difference ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
ID:(7722, 0)
Total heat flow transportation
Exercise 
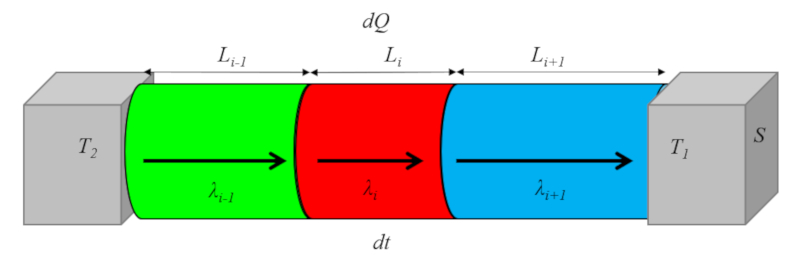
When the material includes multiple conductors connected in series, the total transport coefficient (multiple medium, two interfaces) ($k$) is calculated from the external transmission coefficient ($\alpha_e$), the internal transmission coefficient ($\alpha_i$), the thermal conductivity element i ($\lambda_i$), and the element length i ($L_i$) using the equation:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
This process is illustrated in the following diagram:
ID:(7721, 0)
