$\Delta t = t_2-t_1$

(ID 4131)

$\tau=\displaystyle\frac{t}{2}$

(ID 4136)

Tanto el primer como el ultimo, el quinto, medio son conocidos. En el primer caso se trata del gel que se usa como contacto entre el cuerpo y el transductor. El ultimo medio se asume como aire y corresponde a lo que esta detr s del objeto a estudiar. Los datos de estos medios se pueden obtener de la hoja 'Impedancias' del simulador:

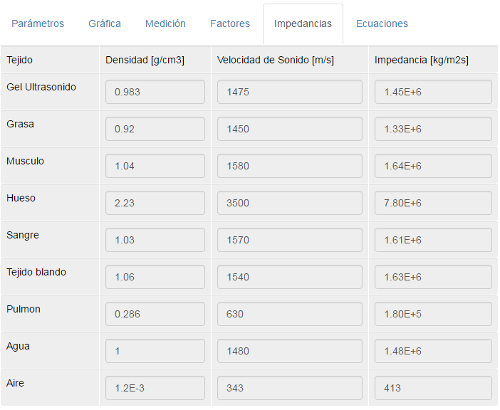
Los datos de densidad y velocidad de sonido deben ser ingresados manualmente al caso mientras que el valor de la impedancia debe ser calculado. La ecuaci n para el calculo de la impedancia se encuentra en la ultima pesta a del simulador.

(ID 9061)

La primera linea de la gr fica de la se al de ultrasonido presenta una amplitud que corresponde al reflejo en la interface entre el primer y segundo medio a_{12}. Dicha amplitud se genera de la amplitud inicial a_0 y el factor de reflexi n R_{12} mediante

a_{12}=R_{12}a_0

con lo que se puede determinar el factor de reflexi n. Una vez se ha calculado este valor se pude determinar la impedancia de la segunda capa ya que

R_{12}=\displaystyle\frac{Z_1-Z_2}{Z_1+Z_2}

Al determinar la impedancia Z_2 se puede, mediante el listado en el simulador, identificar el medio, su velocidad de sonido y densidad que deben ser ingresadas manualmente en el caso.

Una vez que se tiene la velocidad de sonido en el segundo medio es posible estimar el grosor de esta en funci n del correspondiente eco. En este caso el segundo pico de la se al de ultrasonido corresponde a este eco por lo que se puede directamente trabajar con t_2 como el tiempo \tau_2.

(ID 9062)

$\Delta t = n_1t_1+n_2t_2+n_3t_3$

(ID 4134)

$\Delta t = n_1t_1+n_2t_2+n_3t_3+n_4t_4$

(ID 4135)