El hueso
Definición 
Trabajaremos con un hueso y con los escenarios de caída y de golpe. Los parámetros del hueso y de las propiedades del material se resumen aquí:

Geometría y elasticidad
ID:(1556, 0)
La dinámica
Imagen 
Se consideran dos situaciones, la caída (quiebre por pandeo, compresión o flexión) e impacto en la parte central del hueso (quiebre por flexión).

ID:(1557, 0)
Caída y quiebre por pandeo
Nota 
El pandeo es una compresión que se in estabiliza, termina flectando se y puede llevar al quiebre.
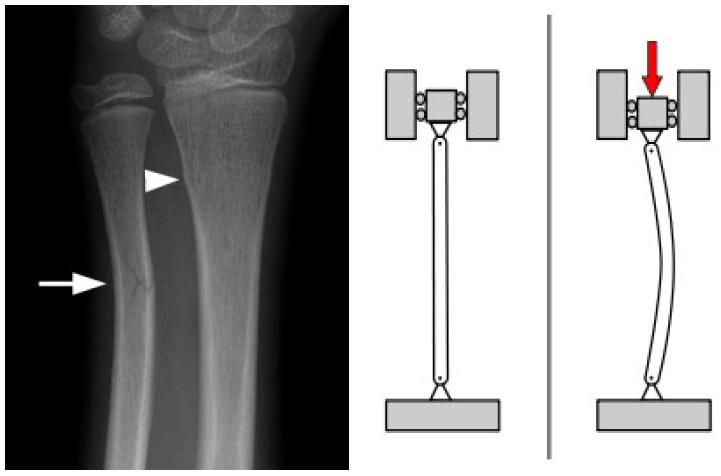
Pregunta de interés: ¿cual es la energía, la tensión, la fuerza y la altura de salto sobre la cual se presentaría pandeo? (
ID:(1558, 0)
Caída y quiebre por compresión o flexión
Cita 
Como el modo de quiebre es aquel que requiere de menor energía, hay que estudiar otras alternativas. Una es que colapse por compresión o que se flecte porque no aterriza en forma perfectamente vertical.
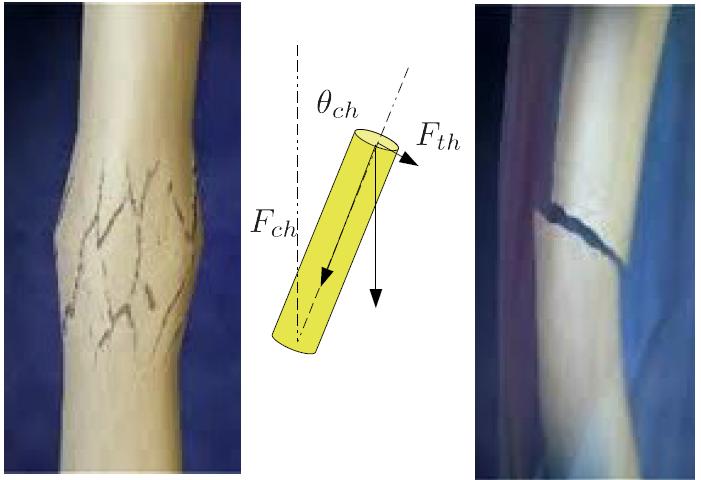
El angulo resulta pequeño por lo que es difícil evitar un quiebre por flexión Fuera de eso la energía para flexionar es muy baja por lo que es muy fácil sufrir un quiebre de este tipo. La pregunta, si logramos caer en forma vertical, cual es la altura máxima de la que podemos saltar.
Pregunta de interés: ¿cual es la energía, la tensión, la fuerza y la altura de salto sobre la cual se presentaría pandeo? (
ID:(1559, 0)
Fractura por impacto
Ejercicio 
Si un jugador recibe un impacto en la mitad del hueso y se considera que el pie, debido a la fricción, y el cuerpo, debido a la inercia, son puntos fijos, se genera una carga que flexiona el hueso.
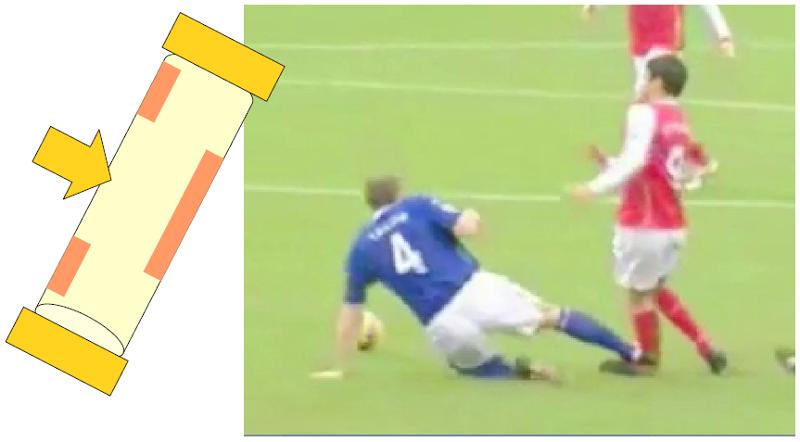
None
Pregunta de interés: ¿Cuál es la energía, la tensión, la fuerza, el desplazamiento y la altura de salto en los que se presentaría el pandeo? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
ID:(1560, 0)
Fragilidad de hueso dañado
Ecuación 
Si el hueso presenta un quiebre existen tensiones altas en la punta de la ruptura. Estas tensiones pueden llevar a un rápido progreso de la ruptura y a la falla catastrófica del hueso:
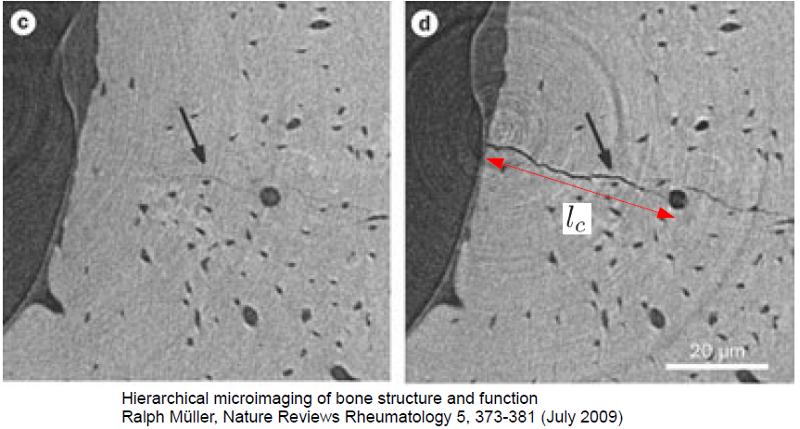
Pregunta de interés: ¿es la fuerza necesaria para hacer progresar la ruptura? (
ID:(1561, 0)
Deportes y Fracturas
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
La variación del trabajo ($\Delta W$) necesaria para que un objeto cambie de la velocidad inicial ($v_0$) a la velocidad ($v$) se obtiene aplicando la fuerza ($F$) que produce un desplazamiento angular la distancia recorrida en un tiempo ($\Delta s$), según:
| $ \Delta W = F \Delta s $ |
Aplicando la segunda ley de Newton para la rotación, en función de la masa inercial ($m_i$) y la aceleración constante ($a_0$):
| $ F = m_i a $ |
esta expresión puede reescribirse como:
$\Delta W = m_i a \Delta s$
o, utilizando la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
obtenemos:
$\Delta W = m_i\displaystyle\frac{\Delta v}{\Delta t} \Delta s$
Si utilizamos la definición de la velocidad angular media ($\bar{\omega}$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
resulta:
$\Delta W = m_i\displaystyle\frac{\Delta v}{\Delta t} \Delta s= m_i v \Delta v$
donde la diferencia de velocidad ($\Delta v$) se expresa como:
| $ dv \equiv v - v_0 $ |
Por otro lado, la velocidad angular puede aproximarse mediante la velocidad angular promedio:
| $ \bar{v} = \displaystyle\frac{ v_1 + v_2 }{2}$ |
Combinando ambas expresiones, se obtiene la ecuación:
$\Delta W = m_i v \Delta v = m_i(v_2 - v_1) \displaystyle\frac{(v_1 + v_2)}{2} = \displaystyle\frac{I}{2}(v_2^2 - v_1^2)$
Por lo tanto, el cambio en la energía se expresa como:
$\Delta W = \displaystyle\frac{I}{2}v_2^2 - \displaystyle\frac{I}{2}v_1^2$
Lo que nos permite definir la energía cinética rotacional como:
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
(ID 3244)
Dado que la fuerza gravitacional es
| $ F_g = m_g g $ |
con $m$ representando la masa. Para mover esta desde una altura $h_1$ a una altura $h_2$, se recorre una distancia de
| $ V = m g ( h_2 - h_1 )$ |
lo que implica que la energ a
| $ dW = \vec{F} \cdot d\vec{s} $ |
con $\Delta s=\Delta h$ nos proporciona la variaci n de la energ a potencial:
$\Delta W = F\Delta s=mg\Delta h=mg(h_2-h_1)=U_2-U_1=\Delta V$
esto lleva a que la energ a potencial gravitacional sea
| $ V = - m_g g z $ |
(ID 3245)
La variación del trabajo ($\Delta W$) necesaria para que un objeto cambie de la velocidad angular inicial ($\omega_0$) a la velocidad angular ($\omega$) se obtiene aplicando un el torque ($T$) que produce un desplazamiento angular la diferencia de ángulos ($\Delta\theta$), según:
| $ \Delta W = T \Delta\theta $ |
Aplicando la segunda ley de Newton para la rotación, en función de el momento de inercia para eje que no pasa por el CM ($I$) y la aceleración angular media ($\bar{\alpha}$):
| $ T = I \alpha $ |
esta expresión puede reescribirse como:
$\Delta W = I \alpha \Delta\theta$
o, utilizando la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
obtenemos:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Si utilizamos la definición de la velocidad angular media ($\bar{\omega}$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
resulta:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
donde la diferencia de velocidades angulares ($\Delta\omega$) se expresa como:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Por otro lado, la velocidad angular puede aproximarse mediante la velocidad angular promedio:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Combinando ambas expresiones, se obtiene la ecuación:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Por lo tanto, el cambio en la energía se expresa como:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Lo que nos permite definir la energía cinética rotacional como:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 3686)
(ID 3702)
(ID 3792)
Ejemplos
Trabajaremos con un hueso y con los escenarios de ca da y de golpe. Los par metros del hueso y de las propiedades del material se resumen aqu :

Geometr a y elasticidad
(ID 1556)
Se consideran dos situaciones, la ca da (quiebre por pandeo, compresi n o flexi n) e impacto en la parte central del hueso (quiebre por flexi n).

(ID 1557)
El pandeo es una compresi n que se in estabiliza, termina flectando se y puede llevar al quiebre.

Pregunta de inter s: cual es la energ a, la tensi n, la fuerza y la altura de salto sobre la cual se presentar a pandeo? (
(ID 1558)
Como el modo de quiebre es aquel que requiere de menor energ a, hay que estudiar otras alternativas. Una es que colapse por compresi n o que se flecte porque no aterriza en forma perfectamente vertical.

El angulo resulta peque o por lo que es dif cil evitar un quiebre por flexi n Fuera de eso la energ a para flexionar es muy baja por lo que es muy f cil sufrir un quiebre de este tipo. La pregunta, si logramos caer en forma vertical, cual es la altura m xima de la que podemos saltar.
Pregunta de inter s: cual es la energ a, la tensi n, la fuerza y la altura de salto sobre la cual se presentar a pandeo? (
(ID 1559)
Si un jugador recibe un impacto en la mitad del hueso y se considera que el pie, debido a la fricci n, y el cuerpo, debido a la inercia, son puntos fijos, se genera una carga que flexiona el hueso.

None
Pregunta de inter s: Cu l es la energ a, la tensi n, la fuerza, el desplazamiento y la altura de salto en los que se presentar a el pandeo? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
(ID 1560)
Si el hueso presenta un quiebre existen tensiones altas en la punta de la ruptura. Estas tensiones pueden llevar a un r pido progreso de la ruptura y a la falla catastr fica del hueso:

Pregunta de inter s: es la fuerza necesaria para hacer progresar la ruptura? (
(ID 1561)
La energía cinética de traslación ($K_t$) se determina en función de la velocidad ($v$) y de la masa inercial ($m_i$), de acuerdo con:
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
5288 se asocia a 6290 y no a 8762, aunque numéricamente sean iguales. La energía que posee un objeto es consecuencia directa de la inercia que fue necesario vencer para lograr su movimiento.
(ID 3244)
El volumen de un cilindro se puede calcular multiplicando la secci n
| $ V = \pi r ^2 h $ |
(ID 3702)
La relaci n entre el ngulo
| $\sin \theta =\displaystyle\frac{ b }{ c }$ |
Para calcular se puede emplear la funci n correspondiente

(ID 3328)
La energía cinética de rotación ($K_r$) es una función de la velocidad angular ($\omega$) y de una medida de la inercia representada por el momento de inercia para eje que no pasa por el CM ($I$):
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
La relaci n entre el ngulo
| $\cos \theta =\displaystyle\frac{ a }{ c }$ |
Para calcular se puede emplear la funci n correspondiente

(ID 3327)
La energía cinética total ($K$) puede tener componentes de traslación y/o de rotación. Por lo tanto, se expresa como la suma de la energía cinética de traslación ($K_t$) y la energía cinética de rotación ($K_r$):
| $ K = K_t + K_r $ |
(ID 3686)
La relaci n entre el ngulo
| $\tan \theta =\displaystyle\frac{ b }{ a }$ |
Para calcular se puede emplear la funci n correspondiente

(ID 3329)
En la superficie del planeta, la fuerza gravitacional es
| $ F_g = m_g g $ |
y la energ a
| $ dW = \vec{F} \cdot d\vec{s} $ |
puede demostrarse que en este caso es
| $ V = - m_g g z $ |
(ID 3245)
ID:(457, 0)
