Der Knochen
Definition 
Wir werden mit einem Knochen und mit den Sturz- und Aufprallszenarien arbeiten. Die Knochenparameter und Materialeigenschaften sind hier zusammengefasst:

Geometrie und Elastizität
ID:(1556, 0)
Die Dynamik
Bild 
Es werden zwei Situationen betrachtet: Sturz (Bruch aufgrund von Knicken, Kompression oder Beugung) und Aufprall auf den zentralen Teil des Knochens (Bruch aufgrund von Beugung).

ID:(1557, 0)
Aufprallbruch
Übung 
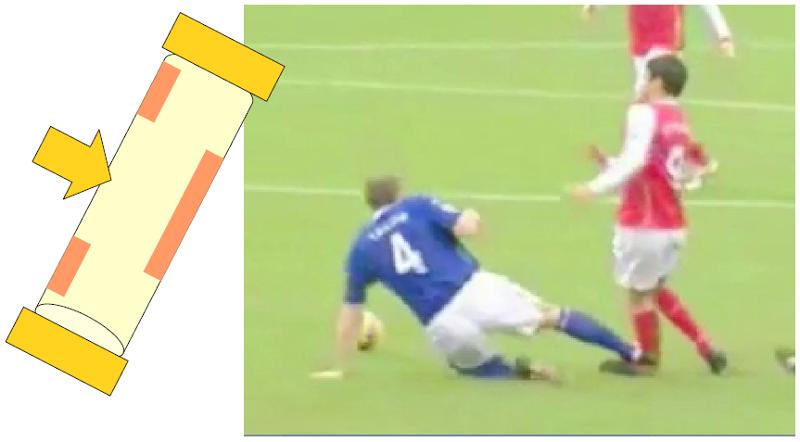
Wenn ein Spieler in der Mitte des Knochens getroffen wird und angenommen wird, dass der Fuß aufgrund von Reibung und der Körper aufgrund von Trägheit feste Punkte sind, entsteht eine Belastung, die den Knochen biegt.
None
Interessante Frage: Welche Energie, Spannung, Kraft, Verschiebung und Sprunghöhe würden zu einem Knicken führen? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
ID:(1560, 0)
Deportes y Fracturas
Storyboard 
Variablen
Berechnungen
Berechnungen
Gleichungen
Die Energie, die erforderlich ist, um ein Objekt von der Winkelgeschwindigkeit $\omega_1$ auf die Winkelgeschwindigkeit $\omega_2$ zu ndern, kann mithilfe der Definition
berechnet werden. Unter Anwendung des zweiten Newtonschen Gesetzes kann diese Gleichung umgeschrieben werden als
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Durch Verwendung der Definition der Winkelgeschwindigkeit
erhalten wir
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
Die Differenz der Winkelgeschwindigkeiten ist
$\Delta\omega=\omega_2-\omega_1$
Andererseits kann die Winkelgeschwindigkeit selbst durch die durchschnittliche Winkelgeschwindigkeit approximiert werden
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Unter Verwendung beider Ausdr cke ergibt sich die Gleichung
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Damit ndert sich die Energie gem
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Wir k nnen dies verwenden, um die kinetische Energie zu definieren
Weil die Gravitationskraft ist
mit $m$ als Masse. Um diese von einer H he $h_1$ auf eine H he $h_2$ zu bewegen, wird eine Strecke von
zur ckgelegt. Daher ergibt sich die Energie
mit $\Delta s=\Delta h$ die Ver nderung der potenziellen Energie:
$\Delta W = F\Delta s=mg\Delta h=mg(h_2-h_1)=U_2-U_1=\Delta V$
somit ist die potenzielle Gravitationsenergie
Die Arbeits Varianz ($\Delta W$), die erforderlich ist, damit ein Objekt von die Anfängliche Winkelgeschwindigkeit ($\omega_0$) auf die Winkelgeschwindigkeit ($\omega$) wechselt, wird durch das Anwenden eines der Drehmoment ($T$) erzeugt, das eine Winkelverschiebung die Differenz von Winkel ($\Delta\theta$) verursacht, gemäß:
Anwendung des zweiten Newtonschen Gesetzes für Rotation in Bezug auf der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) und die Mittlere Winkelbeschleunigung ($\bar{\alpha}$):
kann dieser Ausdruck umgeschrieben werden als:
$\Delta W = I \alpha \Delta\theta$
oder unter Verwendung von die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) und der Abgelaufene Zeit ($\Delta t$):
ergibt sich:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Durch Verwendung der Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) und der Abgelaufene Zeit ($\Delta t$):
resultiert:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
wobei die Unterschied in der Winkelgeschwindigkeiten ($\Delta\omega$) sich ausdrückt als:
Andererseits kann die Winkelgeschwindigkeit durch die durchschnittliche Winkelgeschwindigkeit angenähert werden:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Durch die Kombination beider Ausdrücke ergibt sich:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Daher ergibt sich der Energieänderungsausdruck:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Damit kann die Rotationskinetik wie folgt definiert werden:
Beispiele
Wir werden mit einem Knochen und mit den Sturz- und Aufprallszenarien arbeiten. Die Knochenparameter und Materialeigenschaften sind hier zusammengefasst:
Es werden zwei Situationen betrachtet: Sturz (Bruch aufgrund von Knicken, Kompression oder Beugung) und Aufprall auf den zentralen Teil des Knochens (Bruch aufgrund von Beugung).
Wenn ein Spieler in der Mitte des Knochens getroffen wird und angenommen wird, dass der Fu aufgrund von Reibung und der K rper aufgrund von Tr gheit feste Punkte sind, entsteht eine Belastung, die den Knochen biegt.
Interessante Frage: Welche Energie, Spannung, Kraft, Verschiebung und Sprungh he w rden zu einem Knicken f hren? ($W_{tv}$, $\sigma_{tv}$, $F_{tv}$, $u_{tv}$, $v$).
Die Translational Kinetic Energy ($K_t$) wird in Abhängigkeit von die Geschwindigkeit ($v$) und die Träge Masse ($m_i$) bestimmt, gemäß:
5288 ist mit 6290 und nicht mit 8762 verbunden, auch wenn sie numerisch gleich sind. Die Energie, die ein Objekt besitzt, ist eine direkte Folge der Trägheit, die überwunden werden musste, um seine Bewegung zu erreichen.
$V=\pi r^2h$
Die Beziehung zwischen dem Winkel
Zur Berechnung der entsprechenden Funktion kann verwendet werden
Die Kinetische energie der rotation ($K_r$) ist eine Funktion von die Winkelgeschwindigkeit ($\omega$) und eines Trägheitsmaßes, das durch der Trägheitsmoment für Achse, die nicht durch das CM verläuft ($I$) dargestellt wird:
Die Beziehung zwischen dem Winkel
Zur Berechnung der entsprechenden Funktion kann verwendet werden
Die Gesamte kinetische Energie ($K$) kann aus Translations- und/oder Rotationsanteilen bestehen. Daher ergibt sie sich als Summe von die Translational Kinetic Energy ($K_t$) und die Kinetische energie der rotation ($K_r$):
Die Beziehung zwischen dem Winkel
Zur Berechnung der entsprechenden Funktion kann verwendet werden
An der Oberfl che des Planeten ist die Gravitationskraft
und die Energie
kann gezeigt werden, dass sie in diesem Fall
ist.
ID:(457, 0)
