Camino libre de un fotón
Definición 
Si se indica el camino libre en función de la densidad se le puede comparar entre distintos materiales. Al ser una función de la energía del fotón se obtiene que el camino libre en hueso y agua son en el rango 0 a 10MeV muy similares:
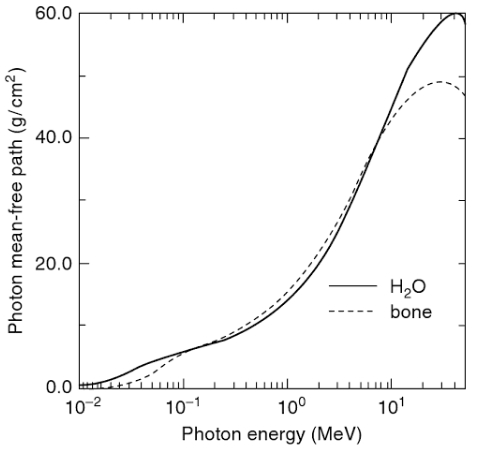
Camino libre de fotones en agua y hueso. The EGS4 Code System Report SLAC-265, Nelson W.R. et. al., Stanford Linear Accelerator Center, California, 1985
Si se desea una estimación del camino libre del fotón en agua, que muestra un comportamiento muy similar al de tejido, basta multiplicar el largo en gramos por centímetro cuadrado por la densidad con lo que se obtiene valores entre 0 y 30 cm.
ID:(9256, 0)
Camino libre de varias partículas
Imagen 
Si se comparan los caminos libres para fotones, neutrones, electrones y protones en agua de observan diferencias en potencias de diez:
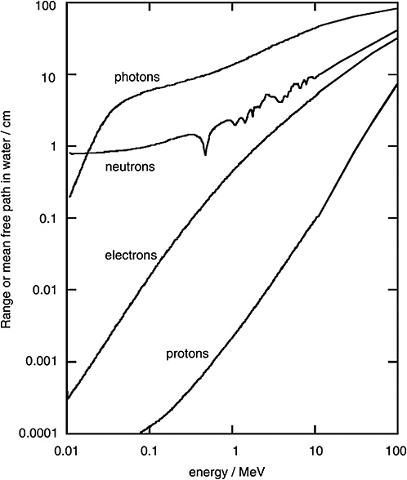
Camino libre de partículas en agua (informe ICRU de 1970).
En este caso los valores están indicados en centímetros. Para el rango de hasta 0.01 a 6 MeV los rangos (en cm) son
Partícula | 0.01 MeV | 6 MeV
-------------|:------------:|:----------:
Fotones | 0.198 | 41.7
Neutrones | 0.878 | 0.430
Electrones | 0.00032 | 0.211
Protones | - | 0.033
ID:(9257, 0)
Distribución de probabilidades para el caso de medio inhomogenio
Nota 
Cuando el medio es inhomogeneo la probabilidad de choque al avanzar en un
equation=9099
el factor
ID:(9353, 0)
Bean machine o tablero de Galton
Cita 
Una aplicación practica del modelo descrito se encuentra en el llamado tablero de Galton. En ella uno deja caer una volita por un tablero de clavos los que hacen que en cada choque la volita cambie de dirección y finalmente llegue abajo a un arreglo en que se le clasifica:
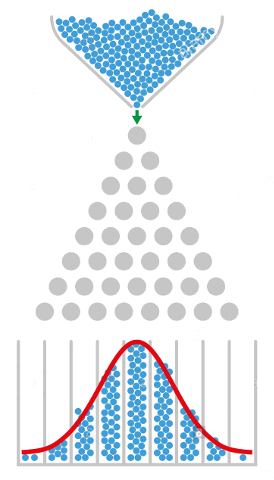
El arreglo en la parte inferior corresponde a la distribución probabilistica
ID:(9254, 0)
Estructura del código (1)
Ejercicio 
La estructura del código de simulación tiene que tener tres unidades básicas:
- la definición de la función distribución (el arreglo que recoge las bolitas en la tabla de Galton)
- el simulador del avance de la partícula que entrega la posición final
- la unidad que determina la clase que debe ser incrementada en la función distribución (la unidad que determina en que contenedor del receptor de bolitas esta es depositada)
Para el primer punto debemos definir un arreglo, que inicialmente se setea en cero, que al final es poblado según la posición alcanzada.
Para el primer paso debemos primero definir el rango en que la bolita pede caer, es decir un valor mínimo
Si el arreglo lo llamamos
```
// set distribution to cero
for(i = 0;i < num;i++){
p[i] = 0.0; // set to empty
}
```
Una ves se han seteado en cero debemos estudiar el comportamiento de
```
Position calculation
```
Una vez se ha obtenido la posición
Con este valor se puede localizar el contenedor
```
cls = round((x-xmin)/Dx); // find position in array
p[cls]++; // increment array p in posicion cls on one
```
en donde la función
ID:(9250, 0)
Estructura del código (2)
Ecuación 
Para calcular las posiciones finales se debe:
- iterar sobre múltiples partículas (N)
- para cada partícula estimar los caminos recorridos
- ir sumando los caminos alternando las direcciones de propagación
En este caso se asume que en cada choque la partícula cambia de dirección de propagación. En su inicio siempre comienza viajando incrementando la distancia lo que se define como la dirección positiva (dir = 1). En cada choque el signo de dir es invertido (dir = -dir o sea si dir=1 este se vuelve dir=-1).
Para el largo del paso se invoca la función de generación de largos antes definida (exprob) que se pondera con la direccón para obtener con la posición anterior la nueva posición.
```
// particles (n de N)
for(n = 0;n < N;n++){
x = 0; // initial position
dir = 1; // initial direction
for(i = 0;i < sp;i++){
x = x + dir*exprob(len); // new position
dir = -dir; // change direction
}
// finish position calculation
// clasification of end position x in distribution p
}
```
ID:(9258, 0)
Simulador camino aleatorio paso variable
Script 
Para obtener la distribución de las partículas en función de la posición se puede realizar una iteración en que
> 0. se define una posición y dirección inicial
> 1. se generado al azar un largo de paso
> 2. se define al azar si se invierte la dirección
> 3. se desplaza según el paso definido en 1 y 2
> 3. se continua en 1
Si se supone que esperamos un tiempo definido y que la partícula se desplaza a velocidad constante, se puede determinar la posición que tiene tras un tiempo dado o tras un camino total definido.
Para comprender como este tipo de simulación depende de los parámetros se propone variar:
> i) la resolución (ancho de la clase con que se estima la distribución)
> ii) numero de iteraciones
ID:(9100, 0)
Conclusiones
Variable 
Jugando con el simulador notamos que
> 1. Solo tiene sentido considerar distribuciones de posiciones posibles
> 2. La distribución se basa en determinar posiciones en rangos discretos
> 3. Rangos de menor tamaño requieren de un mayor numero de iteraciones
ID:(9101, 0)
Modelamiento con material homogéneo (1D)
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
El caso mas simple es el de una particular que se desplaza a lo largo de un eje pudiendo impactar alg n objeto.
Si la probabilidad de lograr llegar a una distancia entre
Si la probabilidad de llegar a
que se puede integrar dando
donde
La funci n
Una distribuci n de esta forma corresponde a una distribuci n de Poisson.
Si se integra la distribuci n
sobre todas las distancias posibles
lo que significa que la funci n esta normalizada. Esto no es de extra arse dando que la funci n
Si se estima el camino medio recorrido ponderando el camino
Con la densidad de probabilidad
se obtiene integrando que
En otras palabras la constante de integraci n
Si se indica el camino libre en funci n de la densidad se le puede comparar entre distintos materiales. Al ser una funci n de la energ a del fot n se obtiene que el camino libre en hueso y agua son en el rango 0 a 10MeV muy similares:
Si se desea una estimaci n del camino libre del fot n en agua, que muestra un comportamiento muy similar al de tejido, basta multiplicar el largo en gramos por cent metro cuadrado por la densidad con lo que se obtiene valores entre 0 y 30 cm.
Si se comparan los caminos libres para fotones, neutrones, electrones y protones en agua de observan diferencias en potencias de diez:
En este caso los valores est n indicados en cent metros. Para el rango de hasta 0.01 a 6 MeV los rangos (en cm) son
Part cula | 0.01 MeV | 6 MeV
-------------|:------------:|:----------:
Fotones | 0.198 | 41.7
Neutrones | 0.878 | 0.430
Electrones | 0.00032 | 0.211
Protones | - | 0.033
Cuando el medio es inhomogeneo la probabilidad de choque al avanzar en un
el factor
Una aplicaci n practica del modelo descrito se encuentra en el llamado tablero de Galton. En ella uno deja caer una volita por un tablero de clavos los que hacen que en cada choque la volita cambie de direcci n y finalmente llegue abajo a un arreglo en que se le clasifica:
El arreglo en la parte inferior corresponde a la distribuci n probabilistica
La estructura del c digo de simulaci n tiene que tener tres unidades b sicas:
- la definici n de la funci n distribuci n (el arreglo que recoge las bolitas en la tabla de Galton)
- el simulador del avance de la part cula que entrega la posici n final
- la unidad que determina la clase que debe ser incrementada en la funci n distribuci n (la unidad que determina en que contenedor del receptor de bolitas esta es depositada)
Para el primer punto debemos definir un arreglo, que inicialmente se setea en cero, que al final es poblado seg n la posici n alcanzada.
Para el primer paso debemos primero definir el rango en que la bolita pede caer, es decir un valor m nimo
Si el arreglo lo llamamos
```
// set distribution to cero
for(i = 0;i < num;i++){
p[i] = 0.0; // set to empty
}
```
Una ves se han seteado en cero debemos estudiar el comportamiento de
```
Position calculation
```
Una vez se ha obtenido la posici n
Con este valor se puede localizar el contenedor
```
cls = round((x-xmin)/Dx); // find position in array
p[cls]++; // increment array p in posicion cls on one
```
en donde la funci n
Para simular el camino recorrido debemos poder generar en forma aleatoria los caminos libres basados en la distribuci n
Para ello basta calcular la probabilidad de lograr un camino
y despejar el camino
se obtiene una ecuaci n que si generamos al azar un numero entre 0 y 1 obtendremos un camino
Con ello se puede definir una funci n:
```
function exprob(len){
var ran = Math.random();
if(ran > 0){
return -len*Math.log(1-ran);
} else {
return len;
}
}
```
en que se considero la generaci n de un numero entre 0 y 1 al azar y se considero la posibilidad de que el valor sea cero lo que generar a problemas ya que el logaritmo ser a menos infinito.
Para calcular las posiciones finales se debe:
- iterar sobre m ltiples part culas (N)
- para cada part cula estimar los caminos recorridos
- ir sumando los caminos alternando las direcciones de propagaci n
En este caso se asume que en cada choque la part cula cambia de direcci n de propagaci n. En su inicio siempre comienza viajando incrementando la distancia lo que se define como la direcci n positiva (dir = 1). En cada choque el signo de dir es invertido (dir = -dir o sea si dir=1 este se vuelve dir=-1).
Para el largo del paso se invoca la funci n de generaci n de largos antes definida (exprob) que se pondera con la direcc n para obtener con la posici n anterior la nueva posici n.
```
// particles (n de N)
for(n = 0;n < N;n++){
x = 0; // initial position
dir = 1; // initial direction
for(i = 0;i < sp;i++){
x = x + dir*exprob(len); // new position
dir = -dir; // change direction
}
// finish position calculation
// clasification of end position x in distribution p
}
```
Para obtener la distribuci n de las part culas en funci n de la posici n se puede realizar una iteraci n en que
> 0. se define una posici n y direcci n inicial
> 1. se generado al azar un largo de paso
> 2. se define al azar si se invierte la direcci n
> 3. se desplaza seg n el paso definido en 1 y 2
> 3. se continua en 1
Si se supone que esperamos un tiempo definido y que la part cula se desplaza a velocidad constante, se puede determinar la posici n que tiene tras un tiempo dado o tras un camino total definido.
Para comprender como este tipo de simulaci n depende de los par metros se propone variar:
> i) la resoluci n (ancho de la clase con que se estima la distribuci n)
> ii) numero de iteraciones
Jugando con el simulador notamos que
> 1. Solo tiene sentido considerar distribuciones de posiciones posibles
> 2. La distribuci n se basa en determinar posiciones en rangos discretos
> 3. Rangos de menor tama o requieren de un mayor numero de iteraciones
ID:(1129, 0)
