User:
Force of gravity and tides in conjunction
Storyboard 
Gravity and centrifugal acceleration generate tides, the movement of oceans that raises and lowers their level with a frequency of 12 hours. Their origin can be generated by both the moon and the sun.
ID:(1523, 0)
Variation of gravity perpendicular to the radius, in conjunction
Image
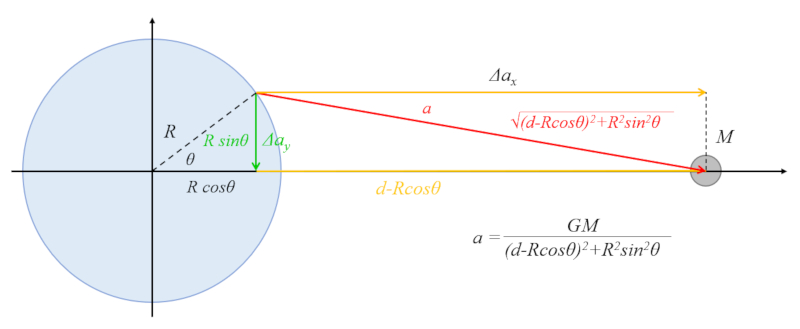
There is a contribution from the gravitational attraction of the celestial body that pulls water towards the equatorial region:
The hypotenuse of the triangle is related to the vertical leg by:
$R\sin\theta$
and the horizontal leg by:
$d - R\cos\theta$
Using the Pythagorean theorem, we have:
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11635, 0)
Variation of gravity parallel to the radius, in conjunction
Image
There is a contribution from the gravitational attraction of the celestial body that pulls water towards the radius, which tends to displace the water towards the equatorial zone:
The hypotenuse of the triangle is formed by the vertical leg:
$R\sin\theta$
and the horizontal leg:
$d - R\cos\theta$
According to the Pythagorean theorem, we have:
$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$
ID:(11658, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$
a_c = G * M /( d ^2+ R ^2-2* d * R *cos( theta ))
$ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cx / a_c = ( d - R * cos( theta ))/sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$
Da_cx = G * M *(1 + 2* R * cos( theta )/ d )/ d ^2
$ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$
Da_cy / a_c = R * sin( theta ) / sqrt( d ^2 + R ^2 - 2 * d * R * cos( theta ))
$ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$
Da_cy = G * M * R * sin( theta )/ d ^3
ID:(15434, 0)
Variation of acceleration perpendicular to the radius, in conjunction
Equation
To determine the variation of the acceleration perpendicular to the radius, we can use triangle similarity to equate the relation
$\displaystyle\frac{\Delta a_{cy}}{a_c}$
with the length
$d-R\cos\theta$
and the hypotenuse
$\sqrt{d^2+R^2-2dR\cos\theta}$
.
By triangle similarity, we have with that
| $ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
.
ID:(11643, 0)
Acceleration perpendicular to the radius, in conjunction
Equation
Con la ley de la gravitación de Newton, con , es:
| $ F = G \displaystyle\frac{ m_g M }{ r ^2}$ |
Se puede, con la definición de la fuerza, con :
| $ F = m_i a $ |
Y el radio al cuadrado:
$r^2=d^2+R^2-2dR\cos\theta$
Calcular la aceleración reemplazando el radio en la fuerza y despejando la aceleración. Esto da con la aceleración:
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
ID:(11644, 0)
Acceleration approximation perpendicular to the radius, in conjunction
Equation
With acceleration generated by the celestial body, en conjunction $m/s^2$, acceleration variation perpendicular to the ecliptic $m/s^2$, angle from the planet line - celestial object $rad$, celestial object planet distance $m$ and planet radio $m$, the relationship between the variation of acceleration and acceleration is:
| $ \displaystyle\frac{ \Delta a_{cy} }{ a_c } =\displaystyle\frac{ R\sin\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
And since the expression for acceleration is with acceleration generated by the celestial body, en conjunction $m/s^2$, angle from the planet line - celestial object $rad$, celestial object planet distance $m$, masa del cuerpo que genera la marea $kg$, planet radio $m$ and universal Gravitation Constant $m^3/kg s^2$:
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
It follows that:
$\Delta a_{cy} = GM\displaystyle\frac{R\sin\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\displaystyle\frac{R\sin\theta}{d}$
Therefore, in the approximation
| $ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$ |
ID:(11645, 0)
Acceleration variation parallel to the radius, in conjunction
Equation
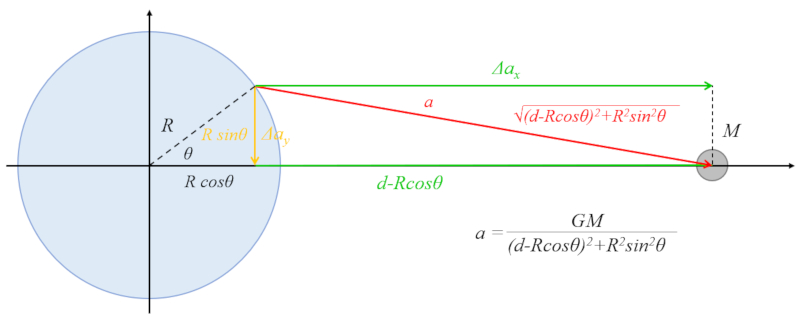
To determine the variation of the acceleration parallel to the radius, we can use triangle similarity to equate the relation
$\displaystyle\frac{\Delta a_{cx}}{a_c}$
with the length
$d+R\cos\theta$
and the hypotenuse
$\sqrt{d^2+R^2-2dR\cos\theta}$
By triangle similarity, we have with that
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
ID:(11647, 0)
Approach acceleration parallel to the radius, in conjunction
Equation
With acceleration generated by the celestial body, en conjunction $m/s^2$, acceleration variation parallel to the ecliptic, in conyunction $m/s^2$, angle from the planet line - celestial object $rad$, celestial object planet distance $m$ and planet radio $m$, the relationship is:
| $ \displaystyle\frac{ \Delta a_{cx} }{ a_c } =\displaystyle\frac{ d - R\cos\theta }{ \sqrt{ d ^2+ R ^2-2 d R \cos \theta } }$ |
And as for acceleration generated by the celestial body, en conjunction $m/s^2$, angle from the planet line - celestial object $rad$, celestial object planet distance $m$, masa del cuerpo que genera la marea $kg$, planet radio $m$ and universal Gravitation Constant $m^3/kg s^2$,
| $ a_c = \displaystyle\frac{ G M }{ d ^2+ R ^2-2 d R \cos \theta }$ |
Thus, we have:
$\Delta a_{cx} =GM\displaystyle\frac{d - R\cos\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1+\displaystyle\frac{2R\cos\theta}{d}\right)$
Therefore, in the approximation
| $ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
ID:(11650, 0)