Usuario:
Condiciones de estabilidad
Storyboard 
Existen distintas estructuras que se forman por efecto de la fuerza de Coriolis y que se pueden caracterizar mediante parámetros que de superarse de forman.
ID:(1582, 0)
Estabilidad: Laminar y turbulencia
Video
Un fluido que se vuelve inestable comienza a formar vórtices y termina mostrando un comportamiento turbulento. La inestabilidad se puede caracterizar mediante el llamado número de Reynolds. En el video se muestra el comportamiento de un líquido en función del número de Reynolds:
ID:(11755, 0)
Estabilidad: numero de Reynold
Ecuación
En el caso del número de Reynolds, se considera cómo un líquido o gas forma vórtices o turbulencias. Para ello, se compara la inercia con la fuerza viscosa. Si la primera se representa con la energía cinética expresada mediante la velocidad
$\rho S R U^2$
y la segunda se representa con la energía asociada a la fuerza viscosa:
$\eta S U$
donde
| $ Re = \displaystyle\frac{ \rho R U }{ \eta }$ |
ID:(11756, 0)
Escala de efectos
Descripción
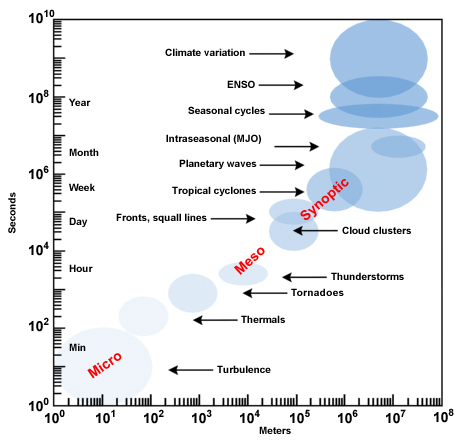
Los sistemas que oscilan se agrupan en dos escalas:
- Fenómenos asociados a la circulación se encuentran en escalas de longitud y tiempo en torno a una velocidad de 1 m/s. Esto abarca desde fenómenos como turbulencias (metros a kilómetros y períodos de segundos a horas) hasta fenómenos meteorológicos (cientos de kilómetros y días a un mes).
- Oscilaciones globales que pueden variar en escala temporal (meses, años), pero la escala espacial es global (zonas o el planeta completo).
ID:(11752, 0)
Estabilidad horizontal: número de Rossby
Ecuación
Para comparar la fuerza de Coriolis con la fuerza inercial, podemos definir su relación como un número adimensional característico conocido como el número de Rossby. Dado que ambas fuerzas dependen de la masa y la velocidad $U$, el número resultante se simplifica a:
 $ R_0 =\displaystyle\frac{ U }{ f R }$ |
La energía asociada a la fuerza de Coriolis se puede estimar considerando la fuerza de Coriolis y una longitud característica $L$. La fuerza de Coriolis es el producto de la masa $m$, el factor de Coriolis $f$ y la velocidad $U$. Por otro lado, la energía asociada a la fuerza inercial es simplemente la energía cinética proporcional a $mU^2$.
En base a esto, el número de Rossby se define como:
$R_0 = \displaystyle\frac{m U^2}{ m f U L}$
Así, el número de Rossby representa la relación entre la energía cinética del fluido y el efecto de la fuerza de Coriolis.
| $ R_0 =\displaystyle\frac{ U }{ f R }$ |
que depende de del factor de Coriolis $f$ y un largo característico $L$.
Al observar esta relación, podemos ver que el número de Rossby representa la proporción entre la velocidad característica del fluido y el efecto de Coriolis. Este número nos indica si el sistema está dominado por la inercia o por la fuerza de Coriolis.
ID:(11753, 0)