Benützer:
Stabilitätsbedingungen
Storyboard 
Es gibt verschiedene Strukturen, die durch die Wirkung der Coriolis-Kraft gebildet werden und die durch Parameter charakterisiert werden können, die sich bilden, wenn sie überwunden werden.
ID:(1582, 0)
Stabilität: Laminar und Turbulenzen
Definition
Ein Fluid, das instabil wird, beginnt sich zu wirbeln und zeigt schließlich ein turbulentes Verhalten. Die Instabilität kann durch die sogenannte Reynolds-Zahl charakterisiert werden. In dem Video wird das Verhalten einer Flüssigkeit in Abhängigkeit von der Reynolds-Zahl gezeigt:
ID:(11755, 0)
Wirkungsskala
Bild
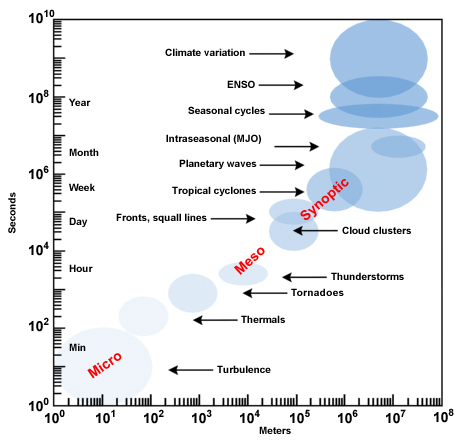
Die schwingenden Systeme lassen sich in zwei Skalen unterteilen:
- Phänomene, die mit der Zirkulation zusammenhängen, treten in Längen- und Zeitskalen um eine Geschwindigkeit von 1 m/s auf. Dies umfasst Phänomene wie Turbulenzen (von Metern bis Kilometern und Zeitspannen von Sekunden bis Stunden) bis hin zu meteorologischen Phänomenen (Hunderte von Kilometern und Tage bis zu einem Monat).
- Globale Schwingungen können sich in zeitlicher Skala (Monate, Jahre) unterscheiden, haben jedoch eine globale räumliche Skala (Regionen oder den gesamten Planeten).
ID:(11752, 0)
Stabilitätsbedingungen
Storyboard
Es gibt verschiedene Strukturen, die durch die Wirkung der Coriolis-Kraft gebildet werden und die durch Parameter charakterisiert werden können, die sich bilden, wenn sie überwunden werden.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Die Energie, die mit der Corioliskraft verbunden ist, kann gesch tzt werden, indem man die Corioliskraft und eine charakteristische L nge $L$ ber cksichtigt. Die Corioliskraft ist das Produkt aus Masse $m$, dem Coriolis-Faktor $f$ und der Geschwindigkeit $U$. Andererseits ist die mit der Tr gheitskraft verbundene Energie einfach die kinetische Energie, proportional zu $mU^2$.
Basierend darauf wird die Rossby-Zahl definiert als:
$R_0 = \displaystyle\frac{m U^2}{ m f U L}$
Die Rossby-Zahl repr sentiert somit das Verh ltnis zwischen der kinetischen Energie der Fl ssigkeit und der Wirkung der Corioliskraft.
Beispiele
Ein Fluid, das instabil wird, beginnt sich zu wirbeln und zeigt schlie lich ein turbulentes Verhalten. Die Instabilit t kann durch die sogenannte Reynolds-Zahl charakterisiert werden. In dem Video wird das Verhalten einer Fl ssigkeit in Abh ngigkeit von der Reynolds-Zahl gezeigt:
Im Fall der Reynolds-Zahl wird betrachtet, wie sich ein Fluid aus Fl ssigkeit oder Gas in Wirbel oder Turbulenzen verwandelt. Daf r wird die Tr gheit mit der viskosen Kraft verglichen. Wenn Ersteres durch die kinetische Energie mit Geschwindigkeit
$\rho S R U^2$
und Letzteres durch die mit der viskosen Kraft verbundene Energie:
$\eta S U$
wobei
Die schwingenden Systeme lassen sich in zwei Skalen unterteilen:
- Ph nomene, die mit der Zirkulation zusammenh ngen, treten in L ngen- und Zeitskalen um eine Geschwindigkeit von 1 m/s auf. Dies umfasst Ph nomene wie Turbulenzen (von Metern bis Kilometern und Zeitspannen von Sekunden bis Stunden) bis hin zu meteorologischen Ph nomenen (Hunderte von Kilometern und Tage bis zu einem Monat).
- Globale Schwingungen k nnen sich in zeitlicher Skala (Monate, Jahre) unterscheiden, haben jedoch eine globale r umliche Skala (Regionen oder den gesamten Planeten).
Um die St rke der Corioliskraft mit der Tr gheitskraft zu vergleichen, k nnen wir ihr Verh ltnis als dimensionslose charakteristische Zahl, bekannt als die Rossby-Zahl, definieren. Da beide Kr fte von Masse und Geschwindigkeit $U$ abh ngen, vereinfacht sich die resultierende Zahl zu:
die vom Coriolis-Faktor $f$ und einer charakteristischen L nge $L$ abh ngt.
Durch Betrachten dieser Beziehung k nnen wir sehen, dass die Rossby-Zahl das Verh ltnis zwischen der charakteristischen Geschwindigkeit der Fl ssigkeit und der Wirkung der Corioliskraft darstellt. Diese Zahl gibt an, ob das System von Tr gheit oder der Corioliskraft dominiert wird.
ID:(1582, 0)