mechanisms

Assim como ocorre com a radia o vis vel, a atmosfera interage com a radia o infravermelha. De maneira semelhante a como a intera o com a atmosfera modelada para a radia o vis vel usando la cobertura visível (VIS) ($\gamma_v$), pode-se introduzir ERROR:7452 que afeta a radia o infravermelha.

Portanto, la intensidade NIR emitida pela Terra para o espaço ($I_{es}$) igual a la intensidade NIR emitida pela Terra ($I_e$) ponderado por um fator que depende de ERROR:7452, de modo que:

equation=10324

Da radia o terrestre $I_e$, que em sua maioria

equation=9950

A fra o da radia o que interage com a atmosfera calculada utilizando a cobertura $\gamma$ atrav s de

equation=9986

Se a Terra est a uma temperatura $T_e$, ela emite radia o de acordo com a lei de Stefan-Boltzmann com uma intensidade dada pela seguinte f rmula:

14479,1

Onde $\sigma$ a constante de Stefan-Boltzmann e $\epsilon$ o coeficiente de emissividade. A constante de Stefan-Boltzmann $\sigma$ tem um valor aproximado de $5.67 \times 10^{-8} W/m^2K^4$, e o coeficiente de emissividade $\epsilon$ representa a efici ncia com que a superf cie da Terra emite radia o, variando de 0 a 1.

A intensidade $I$ emitida por um corpo a uma temperatura $T$ regida pela lei de Stefan-Boltzmann, expressa como:

equation=14479,2

onde $\epsilon$ a emissividade e $\sigma$ a constante de Stefan-Boltzmann. Portanto, no caso da borda inferior da nuvem, que possui uma temperatura $T_b$, a intensidade ser :

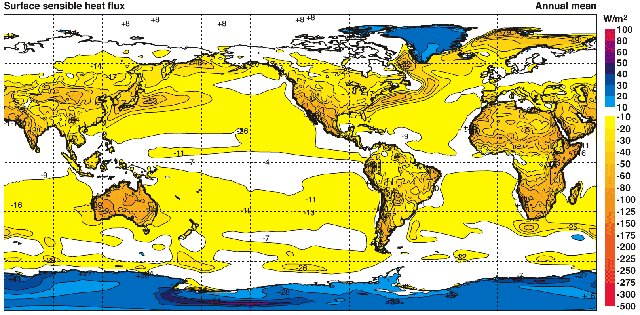
Se observarmos a distribui o do calor transportado por convec o sobre a superf cie do planeta, podemos notar que existem n veis mais ou menos constantes. Por um lado, temos as zonas oce nicas e continentais com um fluxo em torno de $17 W/m^2$ (ascendente) e aproximadamente $-30 W/m^2$ (descendente) em reas cobertas de neve e gelo:

image

Esses dados s o provenientes de uma rean lise de 40 anos realizada por Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, Reino Unido, Projeto de Rean lise do ECMWF (Kallberg et al., 2005).

Ao modelar la energia transmitida por condução e evaporação ($I_d$), pode-se estabelecer uma rela o para o transporte de calor que inclui a diferen a entre ERROR:6516 e la temperatura do fundo da atmosfera ($T_b$), e ERROR:8094, que crucial no processo. A equa o envolve duas constantes, ERROR:8093 e ERROR:6521, de modo que:

equation=9270

ERROR:8093 est na ordem de 10,0 W/m , e ERROR:6521 est na ordem de 0,16 W/m K, com ERROR:8094 tipicamente em torno de 8 m/s.

ERROR:8093 vem principalmente da energia transportada pelo movimento de massas de ar mido, que liberam energia ao se condensarem. ERROR:6521 se origina do transporte de ar atrav s da convec o e da correspondente expans o adiab tica, dependendo principalmente do gradiente de temperatura.

model

La intensidade irradiada ($I_i$) a fra o definida por ERROR:8393 de ERROR:8390, calculada da seguinte maneira:

kyon

La intensidade irradiada ($I_t$) igual a ERROR:8390 reduzido por ERROR:8393, de modo que :

kyon

A Lei de Stefan-Boltzmann estabelece que la intensidade irradiada ($I$) uma fun o de la temperatura ($T$), utilizando as constantes la emissividade ($\epsilon$) e la stefan Boltzmann constant ($\sigma$), da seguinte maneira:

kyon

A Lei de Stefan-Boltzmann estabelece que la intensidade irradiada ($I$) uma fun o de la temperatura ($T$), utilizando as constantes la emissividade ($\epsilon$) e la stefan Boltzmann constant ($\sigma$), da seguinte maneira:

kyon

A Lei de Stefan-Boltzmann estabelece que la intensidade irradiada ($I$) uma fun o de la temperatura ($T$), utilizando as constantes la emissividade ($\epsilon$) e la stefan Boltzmann constant ($\sigma$), da seguinte maneira:

kyon

La energia transmitida por condução e evaporação ($I_d$) depende da diferen a entre la temperatura do fundo da atmosfera ($T_b$) e ERROR:6516, bem como de ERROR:8094 e das constantes ERROR:8093 e ERROR:6521, da seguinte maneira:

kyon