Infrared radiation
Storyboard 
Infrared radiation corresponds mainly to the energy radiated by the earth. A small part of it is irradiated directly into space while the vast majority is absorbed by clouds. These in turn radiate both returned to earth and space. The origin of global warming is mainly a consequence of this flow from the earth to the atmosphere and from the latter to the surface of the earth.
ID:(536, 0)
Emisividad de la tierra
Image 
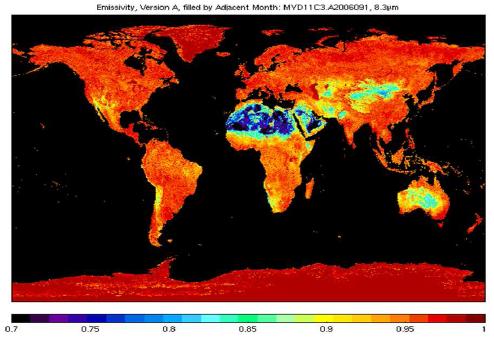
La emisividad de la superficie fluctuar entre 0.7 (océano), 0.8 (desiertos), 0.9 (nieve) y 1.0 (vegetación):
ID:(3073, 0)
Emission NIR intensity from the planet's surface to space
Concept 
Just as with visible radiation, the atmosphere interacts with infrared radiation. Similarly to how the interaction with the atmosphere is modeled for visible radiation using the visible coverage (VIS) ($\gamma_v$), we can introduce ERROR:7452 to affect infrared radiation.
Therefore, the nIR intensity emitted by the earth to space ($I_{es}$) is equal to the nIR intensity emitted by the earth ($I_e$) weighted by a factor that depends on ERROR:7452, so that:
| $ I_{es} =(1- \gamma_i ) I_s $ |
ID:(4677, 0)
Emission intensity NIR from the earth to the atmosphere
Concept 
From the terrestrial radiation $I_e$, which mostly
| $\lambda > 750\,nm$ |
The fraction of radiation that interacts with the atmosphere is calculated using the coverage $\gamma$ through
| $ I_{esa} = \gamma_i I_s $ |
ID:(4684, 0)
Emisión infrarroja de la parte superior de la Atmosfera
Concept 
Si la parte superior de la atmósfera esta a una temperatura
| $\lambda > 750\,nm$ |
según a la ley de Stefan Boltzmann con
| $ I_t = \sigma \epsilon T_t ^4$ |
donde
ID:(4680, 0)
Distribution of heat transported by convection
Description 
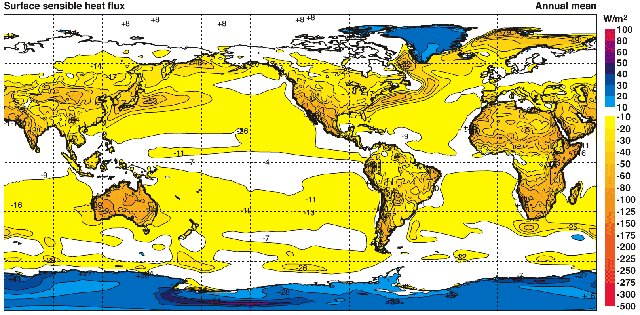
If we observe the distribution of heat transported by convection over the planet's surface, it can be noticed that there are more or less constant levels. On one hand, we have oceanic and continental zones with a flux around $17 W/m^2$ (upward) and approximately $-30 W/m^2$ (downward) in areas covered with snow and ice:
None
These data are derived from a 40-year reanalysis conducted by Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, UK, ECMWF Re-Analysis Project (Kallberg et al., 2005).
ID:(9263, 0)
Emisión onda larga de la tierra en función del tiempo (D0+1)
Php 
Si se observa la radiación de onda larga (NIR) se ve que existe un máximo en torno al mes de agosto/septiembre de todos los años:
Esto se debe a que el hemisferio norte presenta mayor masas continentales por lo que estas reflejan mayormente cuando es verano en dicho hemisferio..
ID:(9324, 0)
Emisión onda larga de la tierra en función de la latitud (D1+0)
Php 
La radiación de onda larga (NIR) es en primera aproximación simétrica en torno al ecuador fuera de presentar un máximo en torno de los grados -20 y +20:
Esto corresponde tanto a la falta de masa continental en torno al ecuador y la baja de intensidad hacia los polos por efecto de la incidencia inclinada de la radiación.
ID:(9325, 0)
Conduction and evaporative flow
Concept 
By modeling the energy transmitted by conduction and evaporation ($I_d$), a relationship for heat transport can be established that includes the difference between ERROR:6516 and the temperature of the lower atmosphere ($T_b$), and ERROR:8094, which is key in the process. The equation involves two constants, ERROR:8093 and ERROR:6521, such that:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
ERROR:8093 is on the order of 10.0 W/m², and ERROR:6521 is on the order of 0.16 W/m²K, with ERROR:8094 typically being around 8 m/s.
ERROR:8093 primarily comes from the energy transported by moving masses of moist air, which release energy when condensed. ERROR:6521 originates from the transport of air through convection and the corresponding adiabatic expansion, so it mainly depends on the temperature gradient.
ID:(15682, 0)
Infrared radiation
Model 
Infrared radiation corresponds mainly to the energy radiated by the earth. A small part of it is irradiated directly into space while the vast majority is absorbed by clouds. These in turn radiate both returned to earth and space. The origin of global warming is mainly a consequence of this flow from the earth to the atmosphere and from the latter to the surface of the earth.
Variables
Calculations
Calculations
Equations
If the Earth is at a temperature $T_s$, it emits radiation, mainly at wavelengths $\lambda > 750$ nm, with a power given by the Stefan-Boltzmann law:
| $ P = \sigma \epsilon S T_s ^4$ |
where $\sigma$ is the Stefan-Boltzmann constant, $\epsilon$ is the emissivity, and $S$ is the emitting surface area.
The intensity of the radiation is defined as the power per unit area, so we can express it as:
| $ I =\displaystyle\frac{ P }{ S }$ |
where $S$ is the emitting area.
Thus, the intensity emitted from the Earth's surface $I_e$ is given by:
| $ I_e = \epsilon \sigma T_e ^4 $ |
where $T_e$ is the temperature and $\epsilon$ is the emissivity of the surface.
(ID 4676)
(ID 9986)
Examples
(ID 15667)

earth009
(ID 3074)
La emisividad de la superficie fluctuar entre 0.7 (oc ano), 0.8 (desiertos), 0.9 (nieve) y 1.0 (vegetaci n):

(ID 3073)

earth011
(ID 3075)
If we observe the distribution of heat transported by convection over the planet's surface, it can be noticed that there are more or less constant levels. On one hand, we have oceanic and continental zones with a flux around $17 W/m^2$ (upward) and approximately $-30 W/m^2$ (downward) in areas covered with snow and ice:

None
These data are derived from a 40-year reanalysis conducted by Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, UK, ECMWF Re-Analysis Project (Kallberg et al., 2005).
(ID 9263)
Si se observa la radiaci n de onda larga (NIR) se ve que existe un m ximo en torno al mes de agosto/septiembre de todos los a os:
Esto se debe a que el hemisferio norte presenta mayor masas continentales por lo que estas reflejan mayormente cuando es verano en dicho hemisferio..
(ID 9324)
La radiaci n de onda larga (NIR) es en primera aproximaci n sim trica en torno al ecuador fuera de presentar un m ximo en torno de los grados -20 y +20:
Esto corresponde tanto a la falta de masa continental en torno al ecuador y la baja de intensidad hacia los polos por efecto de la incidencia inclinada de la radiaci n.
(ID 9325)
By modeling the energy transmitted by conduction and evaporation ($I_d$), a relationship for heat transport can be established that includes the difference between ERROR:6516 and the temperature of the lower atmosphere ($T_b$), and ERROR:8094, which is key in the process. The equation involves two constants, ERROR:8093 and ERROR:6521, such that:
| $ I_d =( \kappa_l + \kappa_c ( T_e - T_b )) u $ |
ERROR:8093 is on the order of 10.0 W/m , and ERROR:6521 is on the order of 0.16 W/m K, with ERROR:8094 typically being around 8 m/s.
ERROR:8093 primarily comes from the energy transported by moving masses of moist air, which release energy when condensed. ERROR:6521 originates from the transport of air through convection and the corresponding adiabatic expansion, so it mainly depends on the temperature gradient.
(ID 15682)
(ID 15678)
ID:(536, 0)
