Mecanismo de conducción de calor
Definición 
Para comprender como se conduce calor en un solido o liquido debemos imaginar que este esta compuesto por particulas (atomos o moleculas) que interactuan y la fuerza que ejercen mutuamente se puede modelar como la generada por un resorte. Dentro de este contexto el calor se puede entender como la energia que tienen las particulas y que se evidencia como osicilacioens. Si los extremos de un cuerpo estan expuestos a distintas temperaturas las respectivas oscilaciones seran de distinta amplitud:
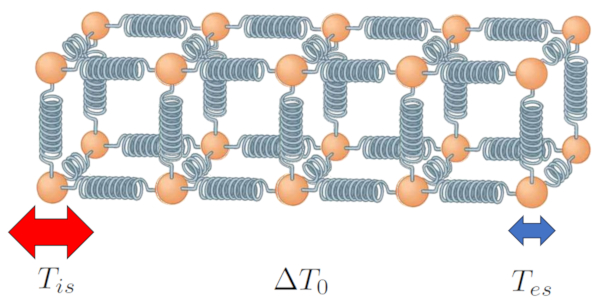
Conducción
Las particulas que oscilan comienzan via las fuerzas que las ligan a propagar la oscilación y con ello la correspondiente energía y temperatura. Con el tiempo toda la cadena presentara oscilacioens que seran mas intensas en el extremo a una temperatura mayor (por ejemplo la temperatura en la superficie interior ($T_{is}$)) y menor en el otro extremo (por ejemplo la temperatura en la superficie exterior ($T_{es}$)).
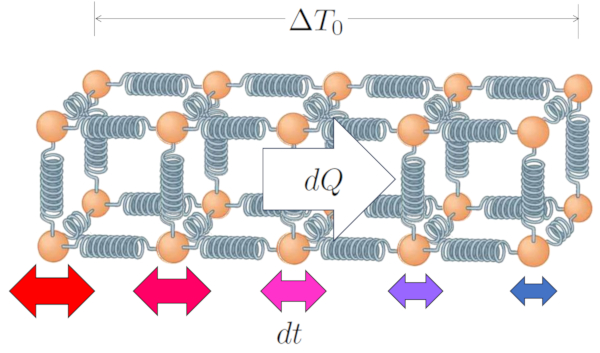
De esta forma la energía, y con ello el calor, se propaga en función de la diferencia de temperatura en el conductor ($\Delta T_0$) que es:
| $ \Delta T_0 = T_{is} - T_{es} $ |
ID:(7718, 0)
Conducción por Medios
Imagen 
El motor de la conducción de calor es la diferencia de temperatura que existe entre los dos extremos de un cuerpo. Si ambas temperaturas son iguales no existiría flujo de calor.
En el caso de calefacción la diferencia de temperatura entre la del agua del calefactor y la temperatura ambiente interior genera el flujo de calor para calentar la habitación. Para calefacción crital el tubo se encuentra inmerso en un cemento que tiene típicamente una constante de conducción $\lambda$ del orden de $1.5,J/m^2sK$. Adicionalmente puede existir un revestimiento con baldosas, con un $\lambda$ de $1,J/m^2sK$ o parqué con un $\lambda$ de $0.17,J/m^2sK$.
> Diferencia de temperatura necesaria
>
> Si se requiere que atraviesen $40,W/m^2$ y se tiene que el coeficiente de conducción es del orden de $1,J/m^2sK$, siendo el grosor de la pared de $1,cm$ se tiene que se requiere de una diferencia de temperatura de
>
>$\Delta T=\displaystyle\frac{L}{\lambda}\displaystyle\frac{\dot{Q}}{S}=\displaystyle\frac{0.01,m}{1,J/m^2sK}\displaystyle\frac{40,W/m^2}{1,m^2}=0.4,K$
>
>Si el grosor de la pared fuera diez veces mayor o la conductividad un décimo se requiere de una diferencia de cuatro grados.
Cabe hacer notar que la diferencia de temperatura aquí calculado es aquel entre las dos superficies del medio. Como la temperatura aumenta/disminuye dentro del medio liquido/gaseoso en contacto, la diferencia total entre ambos medios es mayor a la entre ambas caras del conductor.
ID:(7731, 0)
Transporte de calor
Nota 
El sistema básico incluye una transferencia generada por la diferencia de temperatura ($\Delta T$), que consta de la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$). Por lo tanto:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Con la tasa de flujo de calor ($q$) siendo el responsable de la transferencia entre el interior y el conductor, mediante el coeficiente de transmisión interno ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
La conducción involucra a la conductividad térmica ($\lambda$) y el largo del conductor ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Y la transferencia del conductor al exterior, con el coeficiente de transmisión externo ($\alpha_e$) se representa por:
| $ q = \alpha_e \Delta T_e $ |
Todo esto está representado gráficamente por:
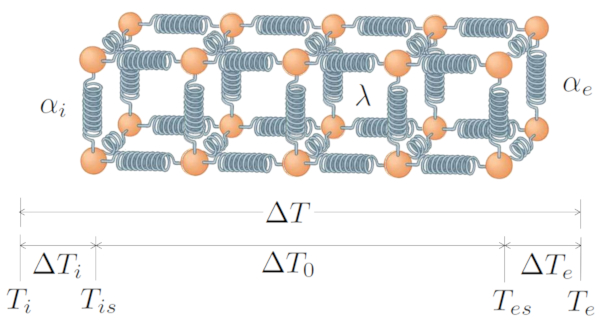
Transferencia de calor
ID:(7723, 0)
Transporte total del flujo de calor
Cita 
Cuando el material incluye múltiples conductores conectados en serie, el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) se calcula a partir de el coeficiente de transmisión externo ($\alpha_e$), el coeficiente de transmisión interno ($\alpha_i$), la conductividad térmica elemento i ($\lambda_i$) y el largo elemento i ($L_i$) utilizando la ecuación:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
Este proceso se ilustra en el diagrama siguiente:
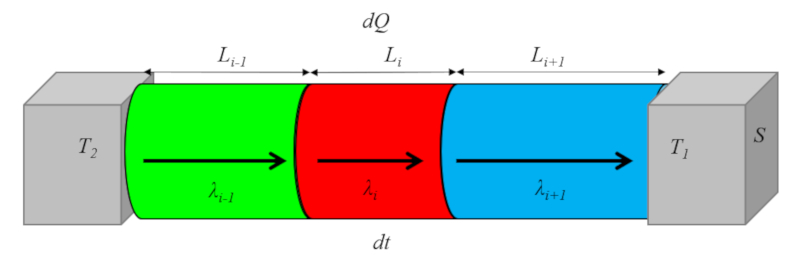
Transporte por un medio
ID:(7721, 0)
Perfil de Temperatura
Ejercicio 
Por lo general, la variación de la temperatura dentro de un conductor es lineal. Sin embargo, en el caso de medios gaseosos y/o líquidos en contacto con el conductor, se produce una gradual variación de la temperatura desde el centro del medio hasta la superficie, como se representa en la siguiente imagen:
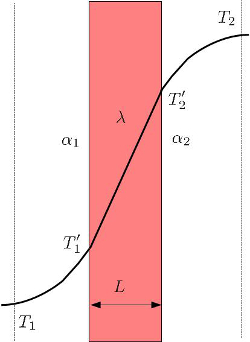
Perfil de temperatura alrededor de un conductor solido
la temperatura en la superficie exterior ($T_{es}$) depende de la temperatura exterior ($T_e$), el coeficiente de total de transporte ($k$), el coeficiente de transmisión externo ($\alpha_e$) y la diferencia de temperatura ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
la temperatura en la superficie interior ($T_{is}$) es una función de la temperatura en el interior ($T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
y la diferencia de temperatura ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
ID:(7722, 0)
Coeficiente de Transporte
Ecuación 
En el caso de la calefacción crital se tiene medios de conducción que colindan por un lado con el agua del tubo de calefacción y por otro lado con el aire de la habitación a calefaccionar. Los coeficientes de transferencia y de conducción se pueden calcular con las ecuaciones vistas.
> Coeficiente de Transferencia del Agua
>
> Los flujos $J_V$ típicos son del orden de 100 l/h. Si el tubo tiene un radio $R_i$ de 6 mm (caso tubo 16x2) esto significa que la velocidad del agua $v$ se puede calcular de
>
> $J_V=S_Vv=\pi R_i^2v$
>
> donde $S_V$ es la sección del tubo. Por ello en el caso de la calefacción crital la velocidad típica es del orden de
>
> $v_w=\displaystyle\frac{J_V}{\pi R_i^2}=\displaystyle\frac{100,l/h}{\pi (6,mm)^2}=0.25,m/s$.
>
> Con ello el coeficiente de transmisión del coeficiente de transmisión de interface con liquido en reposo, que es del orden de $348,J/msK$ y la velocidad de referencia $v_l$ es $0.0278,m/s$ es del orden de
>
> $\alpha_w=\alpha_{w0}\left(1+\sqrt{\displaystyle\frac{v_w}{v_{w0}}}\right)=348,J/m^2sK\left(1+\sqrt{\displaystyle\frac{0.25,m/s}{0.0278,m/s}}\right)=1382,J/m^2sK$.
>
> Coeficiente de Transferencia del Aire
>
> En el caso del aire la velocidad $v_g$ es del orden de cero y con el coeficiente de transferencia de aire en reposo $\alpha_g$ y la velocidad de referencia $v_g$ igual a $1.41,m/s$ con lo que ello el coeficiente de transmisión del orden de
>
>$\alpha_g =\alpha_{g0}\left(1+\displaystyle\frac{v_g}{v_{g0}}\right)=5.6,J/m^2sK\left(1+\displaystyle\frac{0,m/s}{1.41,m/s}\right)=5.6,J/m^2sK$.
Con los coeficientes de transferencia y, asumiendo que el conductor consta de dos medios, se puede calcular la constante de transporte $k$ mediante
$\displaystyle\frac{1}{k}=\displaystyle\frac{1}{\alpha_w}+\displaystyle\frac{1}{\alpha_g}+\displaystyle\frac{L_1}{\lambda_1}+\displaystyle\frac{L_2}{\lambda_2}$
donde los coeficientes de conducción son $\lambda_1$ y $\lambda_2$ en que las capas tienen un grosor $L_1$ y $L_2$.
> Coeficiente de Transporte
>
> En una construcción, la capa en que se encuentran los tubos de la calefacción crital estan a una profundidad $L_1$ de $1,cm$ de la superficie siendo el coeficiente de conductividad $\lambda_1$ del orden de $1,J/m^2sK$. Si adicionalmente consideramo por ejemplo que el piso esta cubeirto por un suelo tipo parque se puede asumir un grosor de $L_2$ de $1,cm$ con un coeficiente de conducción de $0.17,J/m^2sK$.
>
> Con estos datos y los coeficientes de transmisión con los sistemas liquidos y gaseosos se puede calcular el coeficiente de transporte:
>
> $k=\displaystyle\frac{1}{\displaystyle\frac{1}{\alpha_w}+\displaystyle\frac{1}{\alpha_g}+\displaystyle\frac{L_1}{\lambda_1}+\displaystyle\frac{L_2}{\lambda_2}}=\displaystyle\frac{1}{\displaystyle\frac{m^2sK}{1382,J}+\displaystyle\frac{m^2sK}{5.6,J}+\displaystyle\frac{1,cm, msK}{1,J}+\displaystyle\frac{1,cm,msK}{0.17,J}}=4.03,,J/m^2sK$
Cabe hacer notar que la constante de transporte es casi identica con la constante de tranfernecia medio-aire. Esto significa que dicha interface es clave para la operacion del sistema y constituye el cuello de botella del sistema. El segundo factor más importante es el que corresponde a la conductividad del material derevestimiento del piso. De hecho se se varia $\lambda_2$ se obtienen os siguienets constanets de transporte:
$\lambda_2$ ($J/msK$) | 0.2 | 0.4 | 0.6 | 0.8 | 1.0
------------------------------|:----:|:----:|:---:|:----:|:----:
$k$ ($J/m^2sK$) | 4.18 | 4.67 | 4.86 | 4.96 | 5.02
Por otro lado se debe tener presente que este modelo asume que la interface auga-medio y medio-aire tienen lla misma sección lo que no corresponde a la realidad.
ID:(7725, 0)
Simulador de Transporte de Calor
Script 
El simulador de transporte de calor a través de una pared permite estimar los parámetros principales y dibujar el perfil de temperatura a lo largo del sistema.
Existen tres formas de utilizar el simulador:
• Cálculo de la constante de transporte $k$ y la densidad de potencia $\dot{Q}$ alcanzada, dados los valores de temperatura, conductividad térmica $\lambda_i$, espesores de las capas $L_i$, y coeficiente de transferencia $\alpha$. En este caso, seleccione la línea de constante de transporte y densidad de potencia para recalcular y sobrescribir estos valores.
• Calcular el espesor de una de las capas en función de la conductividad térmica de esa capa, así como de los otros parámetros geométricos y materiales del sistema, y de la constante de transporte $k$ o la densidad de potencia $\dot{Q}$. En este caso, seleccione la línea correspondiente a la capa que desea calcular y deje el campo de conductividad térmica vacío.
• Calcular la conductividad térmica de una de las capas en función de su espesor, así como de los otros parámetros geométricos y materiales del sistema, y de la constante de transporte $k$ o la densidad de potencia $\dot{Q}$. En este caso, seleccione la línea correspondiente a la capa que desea calcular y deje el campo de espesor vacío.
Si el sistema externo corresponde a un material diferente, como el suelo en lugar de aire, deje el campo de coeficiente de transferencia vacío.
ID:(7736, 0)
Transporte Calor por Pared
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
Con la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$), la diferencia de temperatura en la interfaz externa ($\Delta T_e$) y la diferencia de temperatura ($\Delta T$), obtenemos
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
que se puede reescribir con la calor transportado ($dQ$), la variación de tiempo ($dt$), la sección ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
y con la conductividad térmica ($\lambda$) y el largo del conductor ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
y
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
como
$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$
lo que resulta en
| $ q = k \Delta T $ |
(ID 7716)
Ejemplos
Para comprender c mo se conduce el calor en un s lido o l quido, podemos imaginar que est compuesto por part culas ( tomos o mol culas) que interact an entre s , ejerciendo fuerzas que pueden modelarse como si estuvieran unidas por resortes. En este marco, el calor se interpreta como la energ a interna de las part culas, la cual se manifiesta en forma de oscilaciones.
Cuando los extremos de un cuerpo est n sometidos a temperaturas diferentes, las part culas en cada extremo vibran con distinta amplitud:

Conducci n
Las part culas que oscilan transmiten su movimiento a las vecinas a trav s de las fuerzas que las enlazan, propagando as la oscilaci n y, con ella, la energ a t rmica. Con el tiempo, toda la cadena de part culas oscilar , pero con amplitudes mayores en el extremo m s caliente (por ejemplo, la temperatura en la superficie interior ($T_{is}$)) y menores en el m s fr o (por ejemplo, la temperatura en la superficie exterior ($T_{es}$)).

De esta manera, la energ a y por lo tanto el calor se transfiere a trav s del cuerpo en funci n del par metro la diferencia de temperatura en el conductor ($\Delta T_0$), que se define por la siguiente expresi n:
| $ \Delta T_0 = T_{is} - T_{es} $ |
(ID 7718)
El flujo de calor ($q$) es una funci n de la conductividad térmica ($\lambda$), el largo del conductor ($L$) y la diferencia de temperatura en el conductor ($\Delta T_0$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
(ID 7712)
El motor de la conducci n de calor es la diferencia de temperatura que existe entre los dos extremos de un cuerpo. Si ambas temperaturas son iguales no existir a flujo de calor.
En el caso de calefacci n la diferencia de temperatura entre la del agua del calefactor y la temperatura ambiente interior genera el flujo de calor para calentar la habitaci n. Para calefacci n crital el tubo se encuentra inmerso en un cemento que tiene t picamente una constante de conducci n $\lambda$ del orden de $1.5,J/m^2sK$. Adicionalmente puede existir un revestimiento con baldosas, con un $\lambda$ de $1,J/m^2sK$ o parqu con un $\lambda$ de $0.17,J/m^2sK$.
> Diferencia de temperatura necesaria
>
> Si se requiere que atraviesen $40,W/m^2$ y se tiene que el coeficiente de conducci n es del orden de $1,J/m^2sK$, siendo el grosor de la pared de $1,cm$ se tiene que se requiere de una diferencia de temperatura de
>
>$\Delta T=\displaystyle\frac{L}{\lambda}\displaystyle\frac{\dot{Q}}{S}=\displaystyle\frac{0.01,m}{1,J/m^2sK}\displaystyle\frac{40,W/m^2}{1,m^2}=0.4,K$
>
>Si el grosor de la pared fuera diez veces mayor o la conductividad un d cimo se requiere de una diferencia de cuatro grados.
Cabe hacer notar que la diferencia de temperatura aqu calculado es aquel entre las dos superficies del medio. Como la temperatura aumenta/disminuye dentro del medio liquido/gaseoso en contacto, la diferencia total entre ambos medios es mayor a la entre ambas caras del conductor.
(ID 7731)
El sistema b sico incluye una transferencia generada por la diferencia de temperatura ($\Delta T$), que consta de la diferencia de temperatura en interfaz interna ($\Delta T_i$), la diferencia de temperatura en el conductor ($\Delta T_0$) y la diferencia de temperatura en la interfaz externa ($\Delta T_e$). Por lo tanto:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Con la tasa de flujo de calor ($q$) siendo el responsable de la transferencia entre el interior y el conductor, mediante el coeficiente de transmisión interno ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
La conducci n involucra a la conductividad térmica ($\lambda$) y el largo del conductor ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Y la transferencia del conductor al exterior, con el coeficiente de transmisión externo ($\alpha_e$) se representa por:
| $ q = \alpha_e \Delta T_e $ |
Todo esto est representado gr ficamente por:
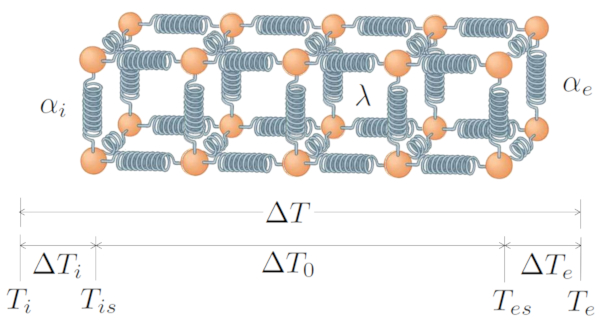
Transferencia de calor
(ID 7723)
Si un medio se desplaza con una constante de el coeficiente de transmisión en liquido, dependiente de la velocidad ($\alpha_{wv}$) y la velocidad del medio ($v_m$) es igual a
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
donde el coeficiente de transmisión en liquido, independiente de la velocidad ($\alpha_{w0}$) representa el caso en el que el medio no se desplaza y el factor velocidad del liquido del coeficiente de transmisión ($v_{w0}$) es la velocidad de referencia.
La constante de transferencia t rmica del material para el caso de un l quido en reposo es igual a $340 J/m^2sK$, mientras que la velocidad de referencia es de $0.0278 m/s$.
(ID 7714)
La transferencia del calor en un medio a otro lleva a que una cantidad de calor
| $\displaystyle\frac{ dQ }{ dt }= \alpha S \Delta T $ |
donde
La constante de transferencia t rmica del material es del orden de 350 - 10000 J/m2sK. Este valor depende de la velocidad si uno de los medios es liquido y se desplaza.
(ID 7713)
Si un medio se desplaza con una constante de el coeficiente de transmisión en gases, dependiente de la velocidad ($\alpha_{gv}$) y la velocidad del medio ($v_m$) es igual a
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
donde el coeficiente de transmisión en gases, independiente de la velocidad ($\alpha_{g0}$) representa el caso en el que el medio no se desplaza y el factor velocidad del gas del coeficiente de transmisión ($v_{g0}$) es la velocidad de referencia.
La constante de transferencia t rmica del material en el caso de un gas en reposo es de $5.6 J/m^2sK$, mientras que la velocidad de referencia es de $1.41 m/s$
(ID 7715)
Cuando el material incluye m ltiples conductores conectados en serie, el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) se calcula a partir de el coeficiente de transmisión externo ($\alpha_e$), el coeficiente de transmisión interno ($\alpha_i$), la conductividad térmica elemento i ($\lambda_i$) y el largo elemento i ($L_i$) utilizando la ecuaci n:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
Este proceso se ilustra en el diagrama siguiente:

Transporte por un medio
(ID 7721)
De esta manera, establecemos una relaci n que nos permite calcular la tasa de flujo de calor ($q$) en funci n de el coeficiente de total de transporte (multiple medio, dos interfaces) ($k$) y la diferencia de temperatura ($\Delta T$):
| $ q = k \Delta T $ |
(ID 7716)
La constante de transporte
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_1 }+\displaystyle\frac{1}{ \alpha_2 }+\displaystyle\frac{ L }{ \lambda }$ |
(ID 7717)
El valor de la tasa de flujo de calor ($q$) en la ecuaci n de transporte se determina utilizando el coeficiente de transmisión interno ($\alpha_i$), el coeficiente de transmisión externo ($\alpha_e$), la conductividad térmica elemento i ($\lambda_i$) y el largo elemento i ($L_i$) de la siguiente forma:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
(ID 7730)
Por lo general, la variaci n de la temperatura dentro de un conductor es lineal. Sin embargo, en el caso de medios gaseosos y/o l quidos en contacto con el conductor, se produce una gradual variaci n de la temperatura desde el centro del medio hasta la superficie, como se representa en la siguiente imagen:

Perfil de temperatura alrededor de un conductor solido
la temperatura en la superficie exterior ($T_{es}$) depende de la temperatura exterior ($T_e$), el coeficiente de total de transporte ($k$), el coeficiente de transmisión externo ($\alpha_e$) y la diferencia de temperatura ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
la temperatura en la superficie interior ($T_{is}$) es una funci n de la temperatura en el interior ($T_i$) y el coeficiente de transmisión interno ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
y la diferencia de temperatura ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
(ID 7722)
En el caso de la calefacci n crital se tiene medios de conducci n que colindan por un lado con el agua del tubo de calefacci n y por otro lado con el aire de la habitaci n a calefaccionar. Los coeficientes de transferencia y de conducci n se pueden calcular con las ecuaciones vistas.
> Coeficiente de Transferencia del Agua
>
> Los flujos $J_V$ t picos son del orden de 100 l/h. Si el tubo tiene un radio $R_i$ de 6 mm (caso tubo 16x2) esto significa que la velocidad del agua $v$ se puede calcular de
>
> $J_V=S_Vv=\pi R_i^2v$
>
> donde $S_V$ es la secci n del tubo. Por ello en el caso de la calefacci n crital la velocidad t pica es del orden de
>
> $v_w=\displaystyle\frac{J_V}{\pi R_i^2}=\displaystyle\frac{100,l/h}{\pi (6,mm)^2}=0.25,m/s$.
>
> Con ello el coeficiente de transmisi n del coeficiente de transmisi n de interface con liquido en reposo, que es del orden de $348,J/msK$ y la velocidad de referencia $v_l$ es $0.0278,m/s$ es del orden de
>
> $\alpha_w=\alpha_{w0}\left(1+\sqrt{\displaystyle\frac{v_w}{v_{w0}}}\right)=348,J/m^2sK\left(1+\sqrt{\displaystyle\frac{0.25,m/s}{0.0278,m/s}}\right)=1382,J/m^2sK$.
>
> Coeficiente de Transferencia del Aire
>
> En el caso del aire la velocidad $v_g$ es del orden de cero y con el coeficiente de transferencia de aire en reposo $\alpha_g$ y la velocidad de referencia $v_g$ igual a $1.41,m/s$ con lo que ello el coeficiente de transmisi n del orden de
>
>$\alpha_g =\alpha_{g0}\left(1+\displaystyle\frac{v_g}{v_{g0}}\right)=5.6,J/m^2sK\left(1+\displaystyle\frac{0,m/s}{1.41,m/s}\right)=5.6,J/m^2sK$.
Con los coeficientes de transferencia y, asumiendo que el conductor consta de dos medios, se puede calcular la constante de transporte $k$ mediante
$\displaystyle\frac{1}{k}=\displaystyle\frac{1}{\alpha_w}+\displaystyle\frac{1}{\alpha_g}+\displaystyle\frac{L_1}{\lambda_1}+\displaystyle\frac{L_2}{\lambda_2}$
donde los coeficientes de conducci n son $\lambda_1$ y $\lambda_2$ en que las capas tienen un grosor $L_1$ y $L_2$.
> Coeficiente de Transporte
>
> En una construcci n, la capa en que se encuentran los tubos de la calefacci n crital estan a una profundidad $L_1$ de $1,cm$ de la superficie siendo el coeficiente de conductividad $\lambda_1$ del orden de $1,J/m^2sK$. Si adicionalmente consideramo por ejemplo que el piso esta cubeirto por un suelo tipo parque se puede asumir un grosor de $L_2$ de $1,cm$ con un coeficiente de conducci n de $0.17,J/m^2sK$.
>
> Con estos datos y los coeficientes de transmisi n con los sistemas liquidos y gaseosos se puede calcular el coeficiente de transporte:
>
> $k=\displaystyle\frac{1}{\displaystyle\frac{1}{\alpha_w}+\displaystyle\frac{1}{\alpha_g}+\displaystyle\frac{L_1}{\lambda_1}+\displaystyle\frac{L_2}{\lambda_2}}=\displaystyle\frac{1}{\displaystyle\frac{m^2sK}{1382,J}+\displaystyle\frac{m^2sK}{5.6,J}+\displaystyle\frac{1,cm, msK}{1,J}+\displaystyle\frac{1,cm,msK}{0.17,J}}=4.03,,J/m^2sK$
Cabe hacer notar que la constante de transporte es casi identica con la constante de tranfernecia medio-aire. Esto significa que dicha interface es clave para la operacion del sistema y constituye el cuello de botella del sistema. El segundo factor m s importante es el que corresponde a la conductividad del material derevestimiento del piso. De hecho se se varia $\lambda_2$ se obtienen os siguienets constanets de transporte:
$\lambda_2$ ($J/msK$) | 0.2 | 0.4 | 0.6 | 0.8 | 1.0
------------------------------|:----:|:----:|:---:|:----:|:----:
$k$ ($J/m^2sK$) | 4.18 | 4.67 | 4.86 | 4.96 | 5.02
Por otro lado se debe tener presente que este modelo asume que la interface auga-medio y medio-aire tienen lla misma secci n lo que no corresponde a la realidad.
(ID 7725)
El simulador de transporte de calor a trav s de una pared permite estimar los par metros principales y dibujar el perfil de temperatura a lo largo del sistema.
Existen tres formas de utilizar el simulador:
• C lculo de la constante de transporte $k$ y la densidad de potencia $\dot{Q}$ alcanzada, dados los valores de temperatura, conductividad t rmica $\lambda_i$, espesores de las capas $L_i$, y coeficiente de transferencia $\alpha$. En este caso, seleccione la l nea de constante de transporte y densidad de potencia para recalcular y sobrescribir estos valores.
• Calcular el espesor de una de las capas en funci n de la conductividad t rmica de esa capa, as como de los otros par metros geom tricos y materiales del sistema, y de la constante de transporte $k$ o la densidad de potencia $\dot{Q}$. En este caso, seleccione la l nea correspondiente a la capa que desea calcular y deje el campo de conductividad t rmica vac o.
• Calcular la conductividad t rmica de una de las capas en funci n de su espesor, as como de los otros par metros geom tricos y materiales del sistema, y de la constante de transporte $k$ o la densidad de potencia $\dot{Q}$. En este caso, seleccione la l nea correspondiente a la capa que desea calcular y deje el campo de espesor vac o.
Si el sistema externo corresponde a un material diferente, como el suelo en lugar de aire, deje el campo de coeficiente de transferencia vac o.
(ID 7736)
ID:(775, 0)
