Wärmeleitungsmechanismus
Definition 
Die Wärme, die von einem
und die Leitfähigkeit
ID:(7718, 0)
Conducción por Suelos
Bild 
El motor de la conducción de calor es la diferencia de temperatura que existe entre los dos extremos de un cuerpo. Si ambas temperaturas son iguales no existiría flujo de calor.
En el caso de calefacción la diferencia de temperatura entre la del agua del calefactor y la temperatura ambiente interior genera el flujo de calor para calentar la habitación. Para calefacción crital el tubo se encuentra inmerso en un cemento que tiene típicamente una constante de conducción $\lambda$ del orden de $1.5,J/m^2sK$. Adicionalmente puede existir un revestimiento con baldosas, con un $\lambda$ de $1,J/m^2sK$ o parqué con un $\lambda$ de $0.17,J/m^2sK$.
> Diferencia de temperatura necesaria
>
> Si se requiere que atraviesen $40,W/m^2$ y se tiene que el coeficiente de conducción es del orden de $1,J/m^2sK$, siendo el grosor de la pared de $1,cm$ se tiene que se requiere de una diferencia de temperatura de
>
>$\Delta T=\displaystyle\frac{L}{\lambda}\displaystyle\frac{\dot{Q}}{S}=\displaystyle\frac{0.01,m}{1,J/m^2sK}\displaystyle\frac{40,W/m^2}{1\m^2}=0.4,K$
>
>Si el grosor de la pared fuera diez veces mayor o la conductividad un décimo se requiere de una diferencia de cuatro grados.
Cabe hacer notar que la diferencia de temperatura aquí calculado es aquel entre las dos superficies del medio. Como la temperatura aumenta/disminuye dentro del medio liquido/gaseoso en contacto, la diferencia total entre ambos medios es mayor a la entre ambas caras del conductor.
ID:(7731, 0)
Wärmetransport
Notiz 
Das grundlegende System umfasst eine Übertragung, die durch die Temperaturdifferenz ($\Delta T$) generiert wird und aus die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) besteht. Daher:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Mit die Wärmestromrate ($q$) als Verantwortlichem für die Übertragung zwischen dem Inneren und dem Leiter, verwendet der Interner Übertragungskoeffizient ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
Die Leitung betrifft die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Und der Transfer vom Leiter nach außen, mit der Externer Transmissionskoeffizient ($\alpha_e$), wird dargestellt durch:
| $ q = \alpha_e \Delta T_e $ |
All dies wird grafisch dargestellt durch:
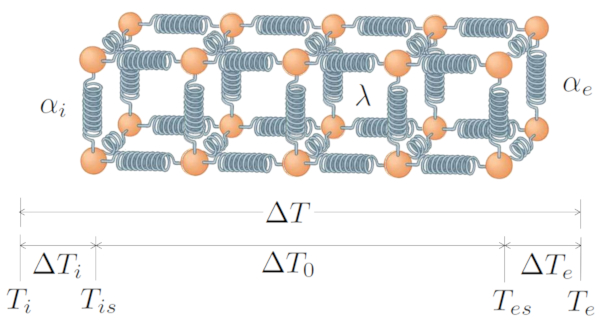
ID:(7723, 0)
Transport des gesamten Wärmeflusses
Zitat 
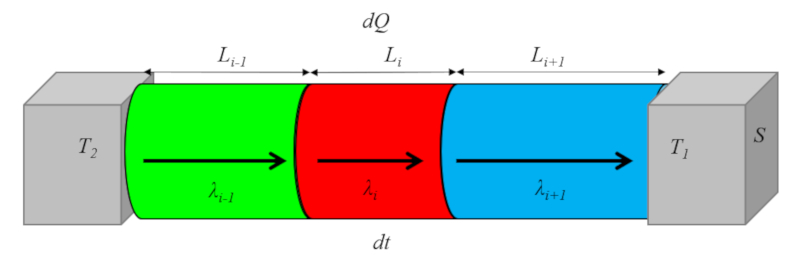
Wenn das Material mehrere in Serie geschaltete Leiter enthält, wird der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) aus der Externer Transmissionskoeffizient ($\alpha_e$), der Interner Übertragungskoeffizient ($\alpha_i$), die Wärmeleitelement i ($\lambda_i$) und der Elementlänge i ($L_i$) mittels der Gleichung berechnet:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
Dieser Prozess wird im folgenden Diagramm dargestellt:
ID:(7721, 0)
Temperaturprofil
Übung 
In der Regel variiert die Temperatur innerhalb eines Leiters linear. Dies gilt jedoch nicht für gasförmige und/oder flüssige Medien, die mit dem Leiter in Kontakt stehen. In diesem Fall gibt es eine allmähliche Temperaturänderung von der Mitte des Mediums zur Oberfläche, wie in folgender Abbildung dargestellt:
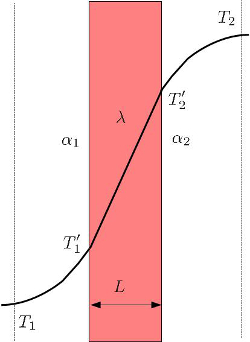
die Äußere Oberflächentemperatur ($T_{es}$) hängt ab von die Außentemperatur ($T_e$), der Koeffizient Gesamttransportation ($k$), der Externer Transmissionskoeffizient ($\alpha_e$) und die Temperaturdifferenz ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
die Innenoberflächentemperatur ($T_{is}$) ist eine Funktion von die Innentemperatur ($T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
und die Temperaturdifferenz ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
ID:(7722, 0)
Coeficiente de Transporte
Gleichung 
En el caso de la calefacción crital uno de los sistemas es agua y el otro aire. En el caso del agua los flujos $J$ típicos son del orden de 100 l/h. Si el tubo tiene un radio $R$ de 8 mm esto significa que la velocidad del agua $v$ se puede calcular de
$J=Sv=\pi R^2v$
donde $S$ es la sección del tubo. Por ello en el caso de la calefacción crital la velocidad típica es del orden de 0.13 m/s. Con ello el coeficiente de transmisión del agua-suelo es del orden de 1075 J/m2sK.
En el caso del aire la velocidad es del orden de cero y con ello el coeficiente de transmisión del orden de 5.4 J/m2sK.
Por ultimo el cemento presenta un coeficiente de 2.3 J/msK. Si la distancia entre tubo y superficie es del orden de 1 cm se tiene que el coeficiente de transporte $k$ es del orden de 5.4 J/m2sK.
ID:(7725, 0)
Wärmetransport-Simulator
Script 
Der Wärmetransport-Simulator durch eine Wand ermöglicht die Schätzung der wichtigsten Parameter und das Erstellen des Temperaturprofils entlang des Systems.
Es gibt drei Möglichkeiten, den Simulator zu verwenden:
• Berechnung der Wärmetransportkonstanten $k$ und der erreichten Leistungsdichte $\dot{Q}$ bei gegebenen Temperaturen, Wärmeleitfähigkeiten $\lambda_i$, Schichtdicken $L_i$ und Übertragungskonstante $\alpha$. In diesem Fall wählen Sie die Zeile für die Wärmetransportkonstante und die Leistungsdichte aus, um diese Werte neu zu berechnen und zu überschreiben.
• Berechnen Sie die Dicke einer der Schichten basierend auf ihrer Wärmeleitfähigkeit sowie anderen geometrischen und materiellen Parametern des Systems und entweder der Wärmetransportkonstanten $k$ oder der Leistungsdichte $\dot{Q}$. In diesem Fall wählen Sie die Zeile für die Schicht aus, die Sie berechnen möchten, und lassen Sie das Feld für die Wärmeleitfähigkeit leer.
• Berechnen Sie die Wärmeleitfähigkeit einer der Schichten basierend auf ihrer Dicke sowie anderen geometrischen und materiellen Parametern des Systems und entweder der Wärmetransportkonstanten $k$ oder der Leistungsdichte $\dot{Q}$. In diesem Fall wählen Sie die Zeile für die Schicht aus, die Sie berechnen möchten, und lassen Sie das Feld für die Dicke leer.
Wenn das externe System einem anderen Material entspricht, wie zum Beispiel Erde anstelle von Luft, lassen Sie das Feld für den Übertragungskoeffizienten leer.
ID:(7736, 0)
Modelo Simplificado
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
Mit die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$), die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und die Temperaturdifferenz ($\Delta T$) erhalten wir
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
die mit die Wärme transportiert ($dQ$), die Zeitvariation ($dt$), die Abschnitt ($S$)
| $ q = \alpha_i \Delta T_i $ |
| $ q = \alpha_e \Delta T_e $ |
und mit die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$)
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
und
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
als
$\Delta T = \Delta T_i + \Delta T_0 + \Delta T_e = \displaystyle\frac{1}{S} \frac{dQ}{dt} \left(\displaystyle\frac{1}{\alpha_i} + \displaystyle\frac{1}{\alpha_e} + \displaystyle\frac{L}{\lambda}\right) = \displaystyle\frac{1}{Sk} \displaystyle\frac{dQ}{dt}$
resultiert in
| $ q = k \Delta T $ |
(ID 7716)
Beispiele
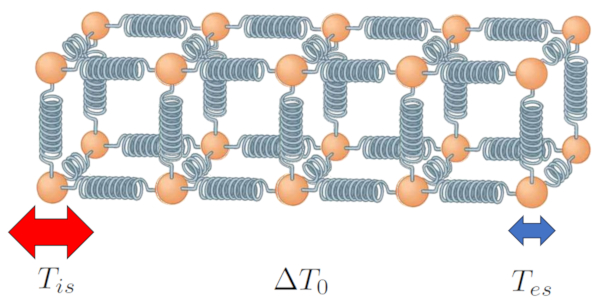
Um zu verstehen, wie W rme in einem Festk rper oder einer Fl ssigkeit geleitet wird, k nnen wir uns vorstellen, dass das Material aus Teilchen (Atomen oder Molek len) besteht, die ber Kr fte miteinander verbunden sind, die wie Federn modelliert werden k nnen. In diesem Zusammenhang wird W rme als die innere Energie der Teilchen verstanden, die sich durch Schwingungen u ert.
Wenn die Enden eines K rpers unterschiedlichen Temperaturen ausgesetzt sind, schwingen die Teilchen an beiden Enden mit unterschiedlicher Amplitude:

Diese schwingenden Teilchen bertragen ihre Bewegung ber die verbindenden Kr fte auf ihre Nachbarn und verbreiten so die Schwingung und die entsprechende thermische Energie. Mit der Zeit beginnt die gesamte Teilchenkette zu schwingen mit gr eren Amplituden am hei eren Ende (z.B. Die Innenoberflächentemperatur ($T_{is}$)) und kleineren Amplituden am k hleren Ende (z.B. Die Äußere Oberflächentemperatur ($T_{es}$)).
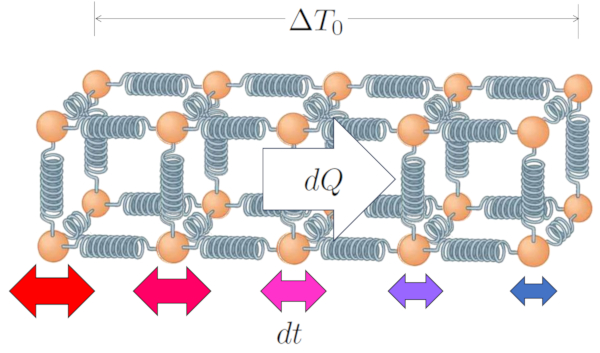
So breitet sich die Energie und damit die W rme im K rper in Abh ngigkeit von die Temperaturunterschied im Leiter ($\Delta T_0$) aus, wie durch die folgende Gleichung beschrieben:
| $ \Delta T_0 = T_{is} - T_{es} $ |
(ID 7718)
Der Wärmefluss ($q$) ist eine Funktion von die Wärmeleitfähigkeit ($\lambda$), der Leitungslänge ($L$) und die Temperaturunterschied im Leiter ($\Delta T_0$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
(ID 7712)
El motor de la conducci n de calor es la diferencia de temperatura que existe entre los dos extremos de un cuerpo. Si ambas temperaturas son iguales no existir a flujo de calor.
En el caso de calefacci n la diferencia de temperatura entre la del agua del calefactor y la temperatura ambiente interior genera el flujo de calor para calentar la habitaci n. Para calefacci n crital el tubo se encuentra inmerso en un cemento que tiene t picamente una constante de conducci n $\lambda$ del orden de $1.5,J/m^2sK$. Adicionalmente puede existir un revestimiento con baldosas, con un $\lambda$ de $1,J/m^2sK$ o parqu con un $\lambda$ de $0.17,J/m^2sK$.
> Diferencia de temperatura necesaria
>
> Si se requiere que atraviesen $40,W/m^2$ y se tiene que el coeficiente de conducci n es del orden de $1,J/m^2sK$, siendo el grosor de la pared de $1,cm$ se tiene que se requiere de una diferencia de temperatura de
>
>$\Delta T=\displaystyle\frac{L}{\lambda}\displaystyle\frac{\dot{Q}}{S}=\displaystyle\frac{0.01,m}{1,J/m^2sK}\displaystyle\frac{40,W/m^2}{1\m^2}=0.4,K$
>
>Si el grosor de la pared fuera diez veces mayor o la conductividad un d cimo se requiere de una diferencia de cuatro grados.
Cabe hacer notar que la diferencia de temperatura aqu calculado es aquel entre las dos superficies del medio. Como la temperatura aumenta/disminuye dentro del medio liquido/gaseoso en contacto, la diferencia total entre ambos medios es mayor a la entre ambas caras del conductor.
(ID 7731)
Das grundlegende System umfasst eine bertragung, die durch die Temperaturdifferenz ($\Delta T$) generiert wird und aus die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) besteht. Daher:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Mit die Wärmestromrate ($q$) als Verantwortlichem f r die bertragung zwischen dem Inneren und dem Leiter, verwendet der Interner Übertragungskoeffizient ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
Die Leitung betrifft die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Und der Transfer vom Leiter nach au en, mit der Externer Transmissionskoeffizient ($\alpha_e$), wird dargestellt durch:
| $ q = \alpha_e \Delta T_e $ |
All dies wird grafisch dargestellt durch:
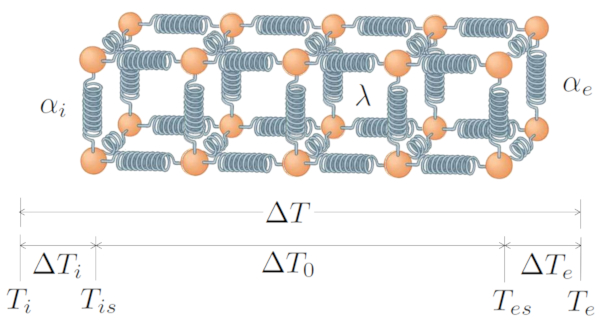
(ID 7723)
Wenn ein Medium mit einer Konstanten von der Durchgangskoeffizient abhängig von der Geschwindigkeit ($\alpha_{wv}$) bewegt wird und die Mittlere Geschwindigkeit ($v_m$) gleich
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
ist, wobei der Durchgangskoeffizient unabhängig von der Geschwindigkeit ($\alpha_{w0}$) den Fall repr sentiert, in dem sich das Medium nicht bewegt, und der Factor Velocidad del Coefiente de Transmisión ($v_{w0}$) die Referenzgeschwindigkeit ist.
Die thermische bertragungskonstante des Materials f r den Fall einer ruhenden Fl ssigkeit betr gt $340 J/m^2sK$, w hrend die Referenzgeschwindigkeit $0,0278 m/s$ betr gt.
(ID 7714)
La transferencia del calor en un medio a otro lleva a que una cantidad de calor
| $\displaystyle\frac{ dQ }{ dt }= \alpha S \Delta T $ |
donde
La constante de transferencia t rmica del material es del orden de 350 - 10000 J/m2sK. Este valor depende de la velocidad si uno de los medios es liquido y se desplaza.
(ID 7713)
Falls ein Medium sich mit einer Konstanten von eine Mittlere Geschwindigkeit ($v_m$) bewegt und der Transmissionskoeffizient in Gasen, abhängig von der Geschwindigkeit ($\alpha_{gv}$) gleich ist
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
wobei der Transmissionskoeffizient in Gasen, unabhängig von der Geschwindigkeit ($\alpha_{g0}$) den Fall repr sentiert, in dem das Medium sich nicht bewegt, und der Transmissionskoeffizient Gasgeschwindigkeitsfaktor ($v_{g0}$) die Referenzgeschwindigkeit ist.
Die thermische Transferkonstante f r das Material im Fall eines ruhenden Gases betr gt $5,6 J/m^2sK$, w hrend die Referenzgeschwindigkeit $1,41 m/s$ betr gt.
(ID 7715)
Wenn das Material mehrere in Serie geschaltete Leiter enth lt, wird der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) aus der Externer Transmissionskoeffizient ($\alpha_e$), der Interner Übertragungskoeffizient ($\alpha_i$), die Wärmeleitelement i ($\lambda_i$) und der Elementlänge i ($L_i$) mittels der Gleichung berechnet:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
Dieser Prozess wird im folgenden Diagramm dargestellt:

(ID 7721)
Auf diese Weise etablieren wir eine Beziehung, die es uns erm glicht, die Wärmestromrate ($q$) als Funktion von der Gesamttransportkoeffizient (mehrere Medien, zwei Schnittstellen) ($k$) und die Temperaturdifferenz ($\Delta T$) zu berechnen:
| $ q = k \Delta T $ |
(ID 7716)
Die Transportkonstante
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_1 }+\displaystyle\frac{1}{ \alpha_2 }+\displaystyle\frac{ L }{ \lambda }$ |
(ID 7717)
Der Wert von die Wärmestromrate ($q$) in der Transportgleichung wird mithilfe von der Interner Übertragungskoeffizient ($\alpha_i$), der Externer Transmissionskoeffizient ($\alpha_e$), die Wärmeleitelement i ($\lambda_i$) und ERROR:9880 < bestimmt /var> wie folgt:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
(ID 7730)
In der Regel variiert die Temperatur innerhalb eines Leiters linear. Dies gilt jedoch nicht f r gasf rmige und/oder fl ssige Medien, die mit dem Leiter in Kontakt stehen. In diesem Fall gibt es eine allm hliche Temperatur nderung von der Mitte des Mediums zur Oberfl che, wie in folgender Abbildung dargestellt:

die Äußere Oberflächentemperatur ($T_{es}$) h ngt ab von die Außentemperatur ($T_e$), der Koeffizient Gesamttransportation ($k$), der Externer Transmissionskoeffizient ($\alpha_e$) und die Temperaturdifferenz ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
die Innenoberflächentemperatur ($T_{is}$) ist eine Funktion von die Innentemperatur ($T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
und die Temperaturdifferenz ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
(ID 7722)
En el caso de la calefacci n crital uno de los sistemas es agua y el otro aire. En el caso del agua los flujos $J$ t picos son del orden de 100 l/h. Si el tubo tiene un radio $R$ de 8 mm esto significa que la velocidad del agua $v$ se puede calcular de
$J=Sv=\pi R^2v$
donde $S$ es la secci n del tubo. Por ello en el caso de la calefacci n crital la velocidad t pica es del orden de 0.13 m/s. Con ello el coeficiente de transmisi n del agua-suelo es del orden de 1075 J/m2sK.
En el caso del aire la velocidad es del orden de cero y con ello el coeficiente de transmisi n del orden de 5.4 J/m2sK.
Por ultimo el cemento presenta un coeficiente de 2.3 J/msK. Si la distancia entre tubo y superficie es del orden de 1 cm se tiene que el coeficiente de transporte $k$ es del orden de 5.4 J/m2sK.
(ID 7725)
Der W rmetransport-Simulator durch eine Wand erm glicht die Sch tzung der wichtigsten Parameter und das Erstellen des Temperaturprofils entlang des Systems.
Es gibt drei M glichkeiten, den Simulator zu verwenden:
• Berechnung der W rmetransportkonstanten $k$ und der erreichten Leistungsdichte $\dot{Q}$ bei gegebenen Temperaturen, W rmeleitf higkeiten $\lambda_i$, Schichtdicken $L_i$ und bertragungskonstante $\alpha$. In diesem Fall w hlen Sie die Zeile f r die W rmetransportkonstante und die Leistungsdichte aus, um diese Werte neu zu berechnen und zu berschreiben.
• Berechnen Sie die Dicke einer der Schichten basierend auf ihrer W rmeleitf higkeit sowie anderen geometrischen und materiellen Parametern des Systems und entweder der W rmetransportkonstanten $k$ oder der Leistungsdichte $\dot{Q}$. In diesem Fall w hlen Sie die Zeile f r die Schicht aus, die Sie berechnen m chten, und lassen Sie das Feld f r die W rmeleitf higkeit leer.
• Berechnen Sie die W rmeleitf higkeit einer der Schichten basierend auf ihrer Dicke sowie anderen geometrischen und materiellen Parametern des Systems und entweder der W rmetransportkonstanten $k$ oder der Leistungsdichte $\dot{Q}$. In diesem Fall w hlen Sie die Zeile f r die Schicht aus, die Sie berechnen m chten, und lassen Sie das Feld f r die Dicke leer.
Wenn das externe System einem anderen Material entspricht, wie zum Beispiel Erde anstelle von Luft, lassen Sie das Feld f r den bertragungskoeffizienten leer.
(ID 7736)
ID:(775, 0)
