Transporte de calor
Storyboard 
O transporte de calor através de um sistema composto por múltiplos meios pode ser estimado analisando como o calor é conduzido em cada meio e transferido em cada interface. O cálculo é realizado utilizando os parâmetros específicos de cada meio e interface, bem como as temperaturas em ambas as extremidades do sistema, fornecendo assim as temperaturas em cada interface.
ID:(1483, 0)
Transporte de calor
Conceito 
O sistema básico inclui uma transferência gerada por la diferença de temperatura ($\Delta T$), que consiste de la diferença de temperatura na interface interna ($\Delta T_i$), la diferença de temperatura no condutor ($\Delta T_0$) e la diferença de temperatura na interface externa ($\Delta T_e$). Portanto:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Com la taxa de fluxo de calor ($q$) sendo responsável pela transferência entre o interior e o condutor, utilizando o coeficiente de transmissão interna ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
A condução envolve la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
E a transferência do condutor para o exterior, com o coeficiente de transmissão externa ($\alpha_e$), é representada por:
| $ q = \alpha_e \Delta T_e $ |
Tudo isso é representado graficamente por:
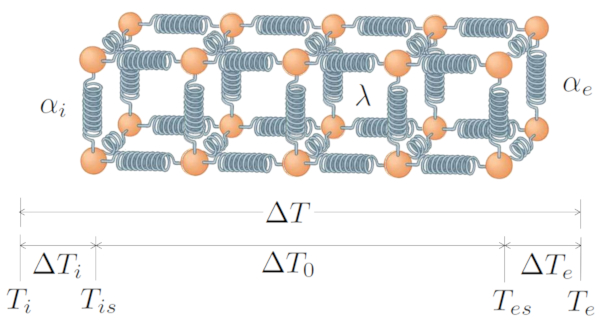
ID:(7723, 0)
Transporte de calor entre dois sistemas através de um terceiro meio
Conceito 
La taxa de fluxo de calor ($q$) é calculado a partir de o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$) e la diferença de temperatura ($\Delta T$) usando a seguinte equação:
| $ q = k \Delta T $ |
onde o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$) é derivado de o coeficiente de transmissão externa ($\alpha_e$), o coeficiente de transmissão interna ($\alpha_i$), la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$) através desta equação:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
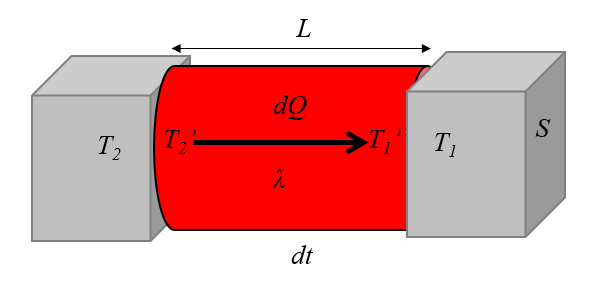
Isso é representado na imagem abaixo:
ID:(1675, 0)
Perfil de temperatura
Conceito 
Normalmente, a variação de temperatura dentro de um condutor segue um padrão linear. No entanto, no caso de meios gasosos e/ou líquidos em contato com o condutor, ocorre uma variação gradual da temperatura do centro do meio até a superfície, como representado na seguinte imagem:

la temperatura da superfície externa ($T_{es}$) é uma função de la temperatura exterior ($T_e$), o coeficiente de transporte total ($k$), o coeficiente de transmissão externa ($\alpha_e$) e la diferença de temperatura ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
la temperatura da superfície interna ($T_{is}$) é uma função de la temperatura interna ($T_i$) e o coeficiente de transmissão interna ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
e la diferença de temperatura ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
ID:(7722, 0)
Transporte total de fluxo de calor
Conceito 
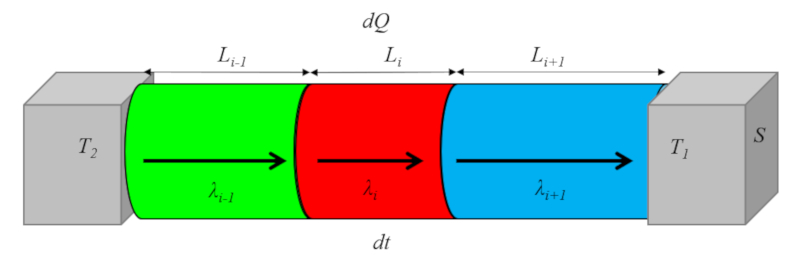
Quando o material inclui múltiplos condutores conectados em série, o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$) é calculado a partir de o coeficiente de transmissão externa ($\alpha_e$), o coeficiente de transmissão interna ($\alpha_i$), la elemento de condutividade térmica i ($\lambda_i$) e o comprimento do elemento i ($L_i$) utilizando a equação:
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
Esse processo é ilustrado no diagrama a seguir:
ID:(7721, 0)
